整数平方根：整数开方及大整数开方解决方法

求整数N的开方，精度在0.001

二分法

若N大于1,则从[1, N]开始，low = 1, high = N, mid = low + (high - low) >> 1开始进行数值逼近

若N小于1,则从[N, 1]开始，low = 0, high = N, mid = low + (high - low) >> 1开始进行数值逼近

#include <stdio.h>  
#include <stdlib.h>  
#include <math.h>  
  
#define ACCURACY 0.001  
  
double newSqrt(double n)  
{  
    double low, high, mid, tmp;  
  
    // 获取上下界  
    if (n > 1)   {  
        low = 1;  
        high = n;  
    } else {  
        low = n;  
        high = 1;  
    }  
  
    // 二分法求开方  
    while (low <= high) {  
        mid = (low + high) / 2.000;  
  
        tmp = mid * mid;  
  
        if (tmp - n <= ACCURACY && tmp -n >= ACCURACY * -1) {  
            return mid;  
        } else if (tmp > n) {  
            high = mid;  
        } else {  
            low = mid;  
        }  
    }  
  
    return -1.000;  
}  
  
int main(void)  
{  
    double n, res;  
  
    while (scanf("%lf", &n) != EOF) {  
        res = newSqrt(n);  
        printf("%lf
", res);  
    }  
  
    return 0;  
}  

牛顿迭代法思路求解：

#include<iostream>
using namespace std;
int main()
{
    int N;
    cout<<"输入N的值：";
    cin>>N

    double x1 = 1;//初值
    double x2 = x1/2.0+N/2.0/x1;
    while( fabs(x2-x1)>0.001)
    {
        x1 = x2;
        x2 = x1/2.0+N/2.0/x1;
    }
    cout<<x1<<endl;

    return 0;
}

整数开方定义

  所谓整数平方根即。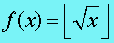

算法

  算法1.猜试法

利用等差级数公式:        

                
  这样的话, 从1开始一直算到数列的前项和第一次大于x的时候,即是所求。下面给出source code(C): 

unsigned linear_search(unsigned long x)
{
    unsigned long sum_n = 1;
    unsigned n = 1;

    if(x <= 1)
    {
        return x;
    }

    while(sum_n <= x)
    {
        n++;
        sum_n += (n<<1) - 1;
    }

    return (n-1);

}

       这种方法无异于穷举法，其唯一的优点是：每次的迭代用到了前面迭代的结果，所以会有一些效率的增益。对于该算法的改进就是不穷举，改用我们熟悉的二分查找法来做。（二分逼近法）

 

unsigned bi_search(unsigned long x)
{
    unsigned long sum_n = 0;
    unsigned n = (x >> 1);
    unsigned top = x;
    unsigned bottom = 0;

    if (x <= 1)
    {
        return x;
    }
    for (;;)
    {
        sum_n = n * n;
        if (sum_n < x)
        {
          bottom = n;
          n += ((top - bottom) >> 1);
          if (n == bottom)
              return n;
        }
        else 
        if (sum_n > x)
        {
          top = n;
          n -= ((top - bottom) >>1);
          if (n == top)
              return n-1;
        }
        else
        {
            return n;
        }
    }
}

 

算法2 Newton 法

把这个问题转换为方程求根问题，即:，求x。

 而方程求根的问题可以用Newton 法来解决。现在的问题有一点不同，即所求的根必须是整数。通过证明，我们可以发现，Newton迭代公式是适用于整数情况的，于是有：

                  
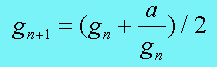
至于是怎么证明的，可以参考hacker’s delight。

另外，初值的选择也是很重要的一环，这里我们选择大于等于的最小的2的幂次数。

OK，下面给出程序：

unsigned newton_method(unsigned long x)
{
    unsigned long x1 = x - 1;
    unsigned s = 1;
    unsigned g0,g1;

    /* 初值设定  通常将初始值设为1，但是只有1的开方才会是1，通过预处理找到更精确地初始值a[n]*/  
    if (x1 > 65535) {s += 8; x1 >>= 16;}
    if (x1 > 255)   {s += 4; x1 >>= 8;}
    if (x1 > 15)    {s += 2; x1 >>= 4;}
    if (x1 > 3)     {s += 1; x1 >>= 2;}

    /*迭代*/
    g0 = 1 << s;
    g1 = (g0 + (x >> s)) >> 1;
    while(g1 < g0)
    {
       g0 = g1;
       g1 = (g0 + x/g0) >> 1;
    }
    return g0;
}

算法3 逐比特确认法

   逐比特确认法认为一个32位整数求根，结果应该是一个16位整数。求这个16位整数，其实质是确认每位的比特是0还是1.我们把这个根分为两个相加的部分，一部分是已确认的值，另一部分是未确认的值。从高位到低位，每次迭代确认一位。初始时，已确认部分为0。则问题的初始形式为：

                       
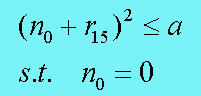
  算法发明者为：James Ulery  论文:Computing Integer Square Roots

下面给出源代码：

unsigned bitwise_verification(unsigned long x)
{

   unsigned long temp = 0;
   unsigned v_bit = 15;
   unsigned n = 0;
   unsigned b = 0x8000;

   if (x <= 1)
       return x;

   do{
       temp = ((n << 1) + b) << (v_bit--);
       if (x >= temp)
       {
           n += b;
           x -= temp;
       }
   }while (b >>= 1);
   
   return n; 
}

性能比较

  在0~1000000范围内对四种算法进行了遍历性的测试，得到测试结果：
      

              
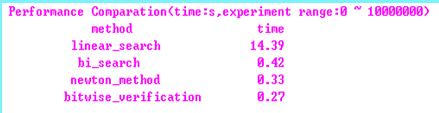
  显见四种算法的遍历性能以逐比特确认法为最好，逐比特确认法从本质上来说是一种二分查找法，而且其查找范围为整个16位整数域；而我们实现的二分查找法的查找范围到已知变量为止，从范围上来说比逐比特确认法来得小，但是最后平均性能却不及逐比特确认法。其原因在于：逐比特确认法把问题分解为相同的子问题的集合，采用递推的方法，很好地利用了前面步骤的结果，不用什么都从头算起，从而避免了重复劳动，用加减法和移位操作代替了乘除法操作，最终获得了性能上的增益。

  需要注意的是，虽然平均性能有如此的关系。并不代表每个数或每组数都有这样的关系。实际上，我们每组产生1000个随机数，并对每组的算法性能进行了测试，各个算法都有获得优胜的时候。至于具体是什么场合用什么算法，需要分析和经验的支撑。目前，我所能归纳出的概要指导准则为：

（1）在大多数情况下，牛顿迭代都能获得不错的性能，

（2）逐比特确认法更适合运算数比较大的场合。

平方根手写算法

      此文算是为大整数开根做好理论准备

     1>    曾经写过迭代求平方根的算法，很是简单。假设求x的平方根，那么可以假设两个非常逼近的数a[n]和a[n+1],它们的平方都非常接近x：

     a[n]*a[n]≈a[n]*a[n+1]≈a[n+1]*a[n+1]≈x;   (1)

     2a[n+1]*a[n]≈a[n]*a[n]+x;                           (2)

     a[n+1]=0.5*(a[n]+x/a[n]);                            (3)

因此求x的平方根，只要有一个初始值，然后用式（3）无限迭代下去就可以就算出足够精度的开方值。迭代求平方根的算法对于浮点数64位范围内的数计算是比较准确且迅速的，C函数库math.h中的sqrt函数貌似就是使用这种算法计算平方根的。

       上述迭代求平方根的算法能够应用到大整数的开根中呢。理论上是没有任何问题的，实际中也是有人就这么做的，并且貌似还很开心的AC了。但使用此算法求大整数开根的话，要实现大整数加法和除法等基本运算，想想还是放弃了。

   2>    接下来介绍一种手动模拟求平方根算法。非常巧妙，非常神奇。可能自己智商有点问题哈，仔细琢磨了几个小时才彻底明白。先仔细介绍如何使用这种算法模拟求平方根，然后再简要说一说它的原理吧！

  （a）首先将要开方根的数从小数点分别向右及向左每两个位一组分开，如98765.432内小数点前的65是一组，87是一组，9是一组，小数点后的43是一组，之后是单独的一个2，要补一个0而得20是一组。

  （b）将最左一组的数减去最接近又不大于它的平方数，并将该平方数的开方（应该是个位数）记下。

  （c) 将上一步所得之差乘以100，和下一组数加起来。

  （d）将记下的数乘以20，然后将它加上某个个位数，再乘以这个个位数，令这个积不大于又最接近上一步所得之差，并将该个位数记下，且将上一步所得之差减去所得之积。

  （e）记下的数依次隔两位记下。

  （f）重复第3步，直到找到答案。

   (g) 可以在数字的最右补上多组的00，以求得理想的精确度未止。

   

原理网上说是（a+b）^2 = a^2 + b^2 + 2ab = a^2 + (2a+b)*b。并没有完全看明白，这里就不班门弄斧了，等以后搞清楚，再补上吧！

/* 大整数开方 ,模拟手工开方*/
# include <stdio.h>
# include <string.h>
# include <stdlib.h>
# include <math.h>
# include <time.h>

# define MAXN 1001

void bigN_sqrt(char *s);
int  bigN_cmp(char *a, char *b, int lim);
void bigN_mul(char *a, int k, int lim);
void bigN_add(char *a, int k);
void bigNN_minus(char *a, char *b, int lim);
int  Newtonsqrt(double x);  //牛顿迭代可求求64位数的平方根 
char str[MAXN];

int main()
{
      freopen("hugeint.in", "r", stdin);
      freopen("hugeint.out", "w", stdout);

    while (~scanf("%s", str))
        bigN_sqrt(str);

 //    printf("time cost %.3lfs.
", (double)clock()/CLOCKS_PER_SEC);
    return 0;
}

int bigN_cmp(char *a, char *b, int lim)
{
    int i;
    for (i = lim-1; i >= 0; --i)
        if (a[i] < b[i]) return 1;
        else if (a[i] > b[i]) return -1;
    return 0;
}
void bigN_mul(char *a, int k, int lim)
{
    int i, tmp, c;
    for (c=i=0; i < lim; ++i) {
        tmp = a[i]*k + c;
        c = tmp / 10;
        a[i] = tmp - 10*c;
    }
}
void bigN_add(char *a, int k)
{
    int i = 0;
    while (k > 0) {
        a[i++] += k%10;
        k /= 10;
    }
}
void bigNN_minus(char *a, char *b, int lim) // b = b - a;
{
    int i, tmp, c;
    for (c=i=0; i < lim; ++i) {
        tmp = b[i] - a[i] + c;
        c = (tmp<0 ? -1:0);
        b[i] = (tmp+10) % 10;
    }
}

int Newtonsqrt(double x)
{
	double x1 = 1;//初值
    double x2 = x1/2.0+x/2.0/x1;
    while( fabs(x2-x1)>0.1)
    {
        x1 = x2;
        x2 = x1/2.0+x/2.0/x1;
    }
    return floor(x1);
}
void bigN_sqrt(char *s)
{
    short int i, k, slen;           // 根的一个十进制位
    char res[MAXN];                 // 试方余数
    char cur[MAXN];                 // 试方上限
    char tmp[MAXN];
    int lim;

    memset(res, 0, sizeof(res));
    memset(cur, 0, sizeof(cur));

    lim = slen = strlen(s);
    if (slen < 18) {               
	//非大整数，直接调用sqrt()计算平方根，结束 。sqrt()计算平方根并非完全正确，在测试的过程中
	// sqrt(8456552264) =  91960 ，而实际上 8456552264的平方根是91959 ，因此采用Newton迭代法求解 
    //    printf("%.0lf
", sqrt(atof(s)));
    //    printf("%.0lf
", sqrt(8456552264));
        double value=atof(s);
        printf("%d",Newtonsqrt(value));
        return ;
    }
    if (slen & 0x1) {
        k = -1;
        cur[0] = s[0] - 48;
    } else {
        k = 0;
        cur[1] = s[0] - 48;
        cur[0] = s[1] - 48;
    }
    while (1) {
        i = 0;
        while (1) {
            ++i;
            memcpy(tmp, res, MAXN);
            bigN_mul(tmp, i*20, lim);
            bigN_add(tmp, i*i);
            if (-1 == bigN_cmp(tmp, cur, lim)) break;     // break until tmp > cur;
        }
        --i;
        printf("%d", i);

        memcpy(tmp, res, MAXN);     //cur -= res*i*20+i*i;
        bigN_mul(tmp, i*20, lim);
        bigN_add(tmp, i*i);
        bigNN_minus(tmp, cur, lim);

        bigN_mul(res, 10, lim);        // res = res*10+i;
        bigN_add(res, i);

        k += 2;
        if (k >= slen) break;
        else {
            bigN_mul(cur, 100, lim);
            bigN_add(cur, ((s[k]-48)*10+(s[k+1]-48)));
        }
    }
    printf("
");
}