what:
QLearning是强化学习算法中value-based的算法,Q即为Q(s,a)就是在某一时刻的 s 状态下(s∈S),采取 动作a (a∈A)动作能够获得收益的期望,环境会根据agent的动作反馈相应的回报reward r,
所以算法的主要思想就是将State与Action构建成一张Q-table来存储Q值,然后根据Q值来选取能够获得最大的收益的动作。
| Q-Table | a1 | a2 |
|---|---|---|
| s1 | q(s1,a1) | q(s1,a2) |
| s2 | q(s2,a1) | q(s2,a2) |
| s3 | q(s3,a1) | q(s3,a2) |
on 和 off policy:是否只使用当前策略所产生的样本,是就是on
Q-Learning 的目的:
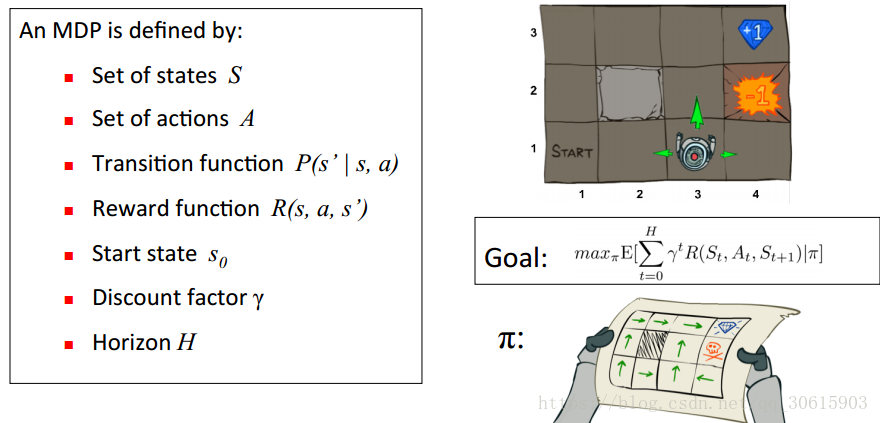

变量分析:
眼前利益 R(S, A)
记忆中的利益
改进的策略为ε-greedy方法:每个状态以ε的概率进行探索,此时将随机选取飞或不飞,而剩下的1-ε的概率则进行开发,即按上述方法,选取当前状态下效用值较大的动作。
Q-learning的主要优势就是使用了时间差分法TD(融合了蒙特卡洛和动态规划)能够进行离线学习, 使用bellman方程可以对马尔科夫过程求解最优策略
一、Bellman Equation for MRPs
首先我们从value function的角度进行理解,value function可以分为两部分:
- 立即回报
- 后继状态的折扣价值函数
见下面的推导公式:

我们直接从第一行到最后一行是比较好理解的,因为从状态s到状态s+1,是不确定,还是之前的例子,比如掷骰子游戏,当前点数是1的情况下,下一个状态有可能是1,2,3,4,5,6的任意一种状态可能,所以最外层会有一个期望符号。
如果我们跟着一直推下来的话:有疑问的会在导出最后一行时,将 变成了
。其理由是收获的期望等于收获的期望的期望。参考叶强童鞋的理解。
则最后我们得到了针对MRP的Bellman方程:

通过方程可以看出 由两部分组成,一是该状态的即时奖励期望,即时奖励期望等于即时奖励,因为根据即时奖励的定义,它与下一个状态无关;这里解释一下为什么会有期望符合,是因为从状态s的下一个状态s+1可能有多个状态,比如掷骰子,下一个状态可能有1,2,3,4,5,6,从s到下一个状态都是有一定概率,所以会有期望符合。
另一个是下一时刻状态的价值期望,可以根据下一时刻状态的概率分布得到其期望,比如在上面掷骰子例子中,从状态1到下一个状态1,2,3,4,5,6求期望的做法,我们可以直接用概率公式 然后乘以对应下一状态的价值函数即可。
如果用s’表示s状态下一时刻任一可能的状态,那么Bellman方程可以写成:
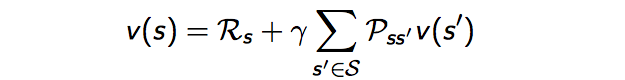
完整的slides如下:
