文章真是经典!
原文:http://www.cnblogs.com/microgrape/archive/2011/05/11/2043799.html
其实二叉树的遍历,这么经典的东西,我自己一直都不明白。递归算法那么简洁,让人神魂颠倒;非递归算法就那么不好理解。。。最近使劲想了一想,似乎有一些眉目了,于是记录下来。
【思想】
(1)递归思想。虽然非递归算法没有直接使用函数递归,但是使用了栈,所以实际上仍然是递归的思想。但是它递归的是那么朦胧,让人无法捉摸。可以从以下几个方面思考:首先,三个非递归遍历的算法开始都是向左走到树的最左下方的节点,并把路上遇到的节点入栈,这其实就是递归中的前一半过程。如下图所示:
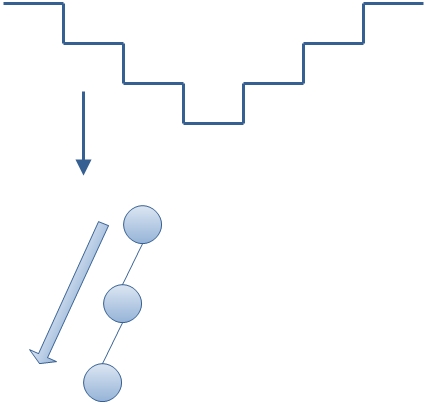
图中上半部分表示了一个递归函数的层层深入的栈结构,下面则是模拟了将二叉树的节点入栈的过程。以此类推,从最左下的节点向上的过程就是退栈的过程,也就是图上半部分的右边。
(2)算法中cur节点的实际意义。在下面的代码中,可以看到三个算法(前、中、后序)中都有一个cur节点。这个节点表示什么含义呢?就是表示发现了一个继续入栈的机会,也就是从这个节点开始,又可以重复向左下走到底。所以中序遍历和后序遍历的开始都有一句:
while( ! s.empty() || cur != NULL )
那么当cur为空,也就是没有可以继续入栈的机会的时候,那就得靠栈中存着的余货了。
对中序遍历来说,访问完当前节点之后,如果它没有右孩子,那就没有继续入栈的机会了,只能退栈。
对后序遍历来说,检查当前节点时,如果当前节点没有右孩子或者它的右孩子刚刚被访问,那么也别无选择,只能退栈。
这也就是它们的代码中把相应的cur置为NULL的原因。
【代码】
#include <iostream> #include <stack> #include <vector> #include <iomanip> #include <queue> using namespace std; struct Node { Node( const Node *t ) : data( t->data ), lChild( NULL ), rChild( NULL ) {} Node( int d ) : data( d ), lChild( NULL ), rChild( NULL ) {} struct Node* lChild; struct Node* rChild; int data; }; void PreOrder( Node *root, void (*visit)(Node*) ) //ps:二叉树的先序遍历与二叉树的深度优先遍历什么关系呢? { if( root == NULL ) return; stack<Node*> s; Node *cur; s.push( root ); while( !s.empty() ) { cur = s.top(); visit( cur ); s.pop(); if( cur->rChild != NULL ) s.push( cur->rChild ); if( cur->lChild != NULL ) s.push( cur->lChild ); } } void InOrder( Node *root, void (*visit)(Node*) ) { stack<Node*> s; Node *cur = root; while( ! s.empty() || cur != NULL ) { while( cur != NULL ) { s.push( cur ); cur = cur->lChild; } cur = s.top(); visit( cur ); s.pop(); if( cur->rChild == NULL ) cur = NULL; // no current node. must pop. else cur = cur->rChild; } } void PostOrder( Node *root, void (*visit)(Node*) ) { stack<Node*> s; Node *cur = root; Node *visited = NULL; while( ! s.empty() || cur != NULL ) { while( cur != NULL ) { s.push( cur ); cur = cur->lChild; } cur = s.top(); // check but no visit. if( cur->rChild == visited || cur->rChild == NULL ) { visit( cur ); s.pop(); visited = cur; cur = NULL; // no current node, must pop. } else cur = cur->rChild; } } /*************************************** * 层序遍历:跟先序遍历很像。是二叉树的广度优先搜索。 * 所以要用队列实现。 ***************************************/ void LevelOrderTraverse(Node* t, void (*visit)(Node* ) ) { if(NULL == t) return; queue<Node*> q; Node* e; q.push(t); while(!q.empty()) { visit(e = q.front()); q.pop(); if(NULL != e->lChild) q.push(e->lChild); if(NULL != e->rChild) q.push(e->rChild); } } //插入节点的函数 void insert(Node *&root, Node *t) { if( root == NULL ) root = new Node( t ); else if ( t->data > root->data ) insert( root->rChild, t ); else if ( t->data < root->data ) insert( root->lChild, t ); else ; } //使用数组创建二叉树 Node* createTree( vector<int>& a) { if( 0 == a.size() ) return NULL; Node *root = new Node(a[0]); vector<int>::const_iterator iter = a.begin(); iter++; for ( ; iter != a.end() ; ++iter ) { Node *t = new Node( *iter ); insert( root, t ); } return root; } void visit(Node *t) { cout<<setw(3)<<t->data<<" "; }
下面是主函数:
int main() { vector<int> a; for (int i = 0 ; i < 10 ; ++i ) { int temp = rand()%31;//随便取了几个随机数 a.push_back(temp); } Node* root = createTree( a ); PreOrderTraverse(root, visit); cout<<endl; InOrderTraverse(root, visit); cout<<endl; PostOrderTraverse(root, visit); cout<<endl; }