先更热身赛。
(T2T3) 只是测试题,就不说了。(交互日常不会写, (linux) 日常不会)
(T1) 的思路还是很好的,考场上没想出来,在 (EIls) 的点拨(下面这句话)下逐渐找到了方向。

(为保护 (EIls) 隐私已将昵称和头像撤下)
在应对这一类题目的时候,我们有一个经典的东西来处理它-----序列自动机。
而序列自动机的本质是一个 (DP) ,记 (f[i]) 为以字符 (i) 结尾的本质不同的子序列的个数。那么我们可以把 (f) 看作是一个行向量,那么,每次向后添加一个字符,就是乘以一个矩阵,可以发现矩阵是这样的:
左上-右下对角线上是 (1) ,第 (i)(假设添加的这个字符是 (i) )列是 (1) ,其余是 (0) .
然后考虑乘起来,暴力乘是 (2^n) 的,显然过不了。
我们把乘的过程看作是一棵树,这里用 (uoj) 上题目中的样例表示一下:
样例:3
a,b,c。
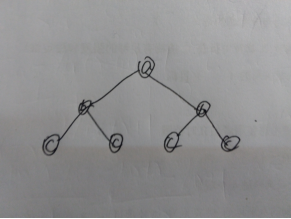
在树上dfs的话还是 (2^n) 的。
但是,可以发现一个事实,这棵树是对称的,我们不需要把整个树存下来,只要存我当前的乘到的子树就可以了,因为另一棵子树和我相同,而在乘的过程中依次访问的子树的根就是输入的操作序列的倒序。
一共乘 (n) 次,每次乘的操作次数是字符集大小的 (3) 次方,操作次数(2 imes n imes (字符集大小)^3),估算一下是 (175760000) ,还是有一点吃紧的。
因为不太熟悉复杂度的具体定义,以及之前看到有人在 (luogu) 上乱用复杂度被D的, 所以部分地方用的是"操作次数"一词,和复杂度的差别是考虑了常数,使用这个词也是为了凸显常数的影响。
来更正赛了。
说明:不更无法通过传统算法竞赛方法通过的题目(B)。
A.场切了,就是dp,dp[i][j]表示到第i个字符,目前已经匹配到"xxxll"的第j个字符的最小修改次数。
C.自己没实现,据出题人说是dfs+估价函数,估价函数是当我走到不能再走的时候我手中三种钥匙的最小值。
D.思路很妙的DP,首先发现一边最多只有一个棋子没有圣盾(我考场上就只想到了这里),令dp[n][m][0/1][0/1]表示当前进攻方有n个棋子,防守方有m个棋子,进攻方的当前进攻棋子是(1)否(0)有圣盾,防守方是(1)否(0)全部有圣盾,如果防守方有一个没圣盾,那么它一定是上一轮攻击的那个。
离谱的是,我们发现这样是可以转移的(这是真的离谱,兄弟),我来画一下转移图。
对不起,这篇文章咕了。