二叉树

一、参考

Binary search trees explained

二叉树基础

二、二叉查找树 binary search tree

2.1 定义

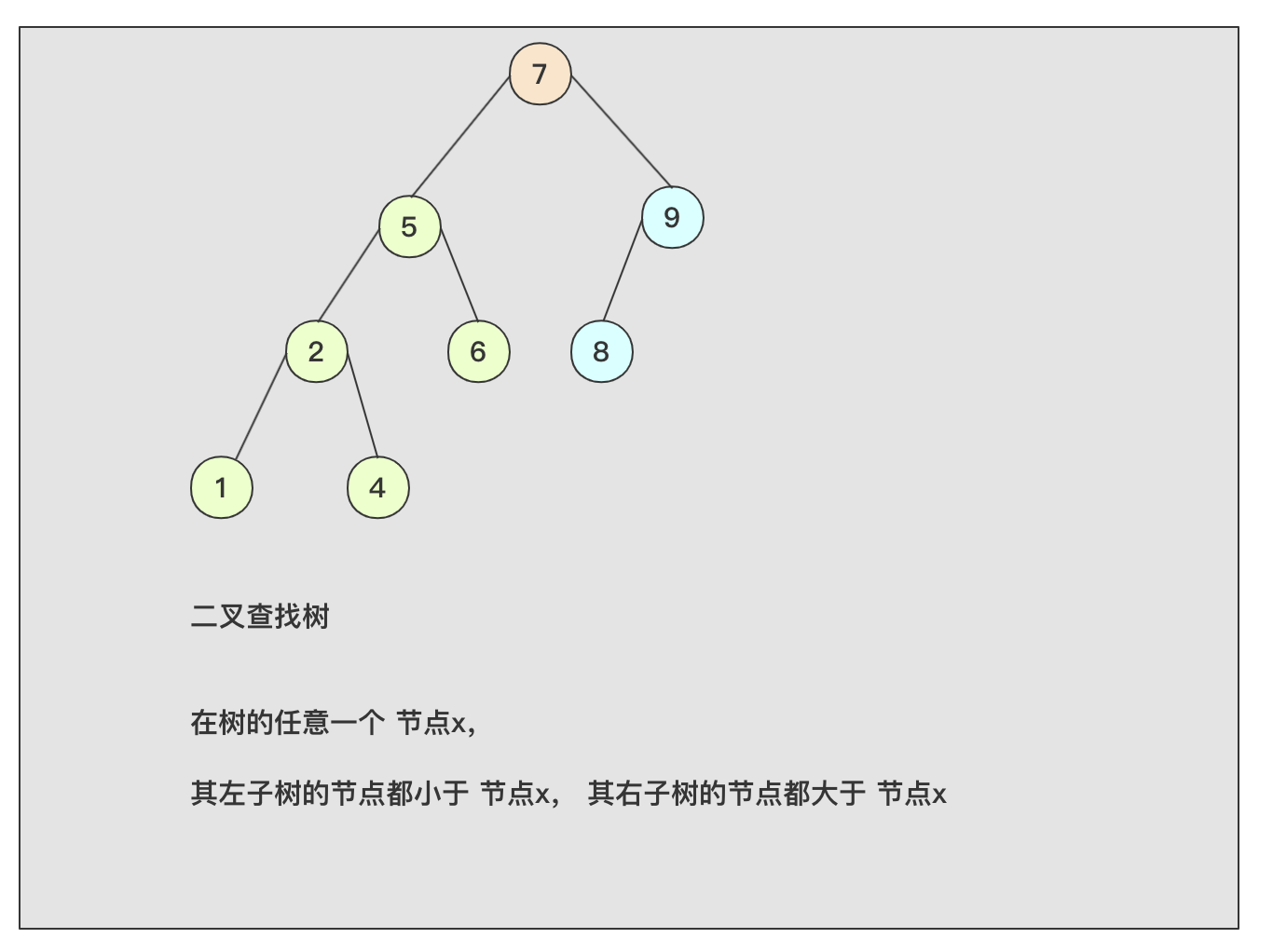
A binary search tree (BST) is a binary tree where each node has a Comparable key (and an associated value) and satisfies the restriction that the key in any node is larger than the keys in all nodes in that node’s left subtree and small- er than the keys in all nodes in that node’s right subtree

三、 操作

3.1 查找

/*

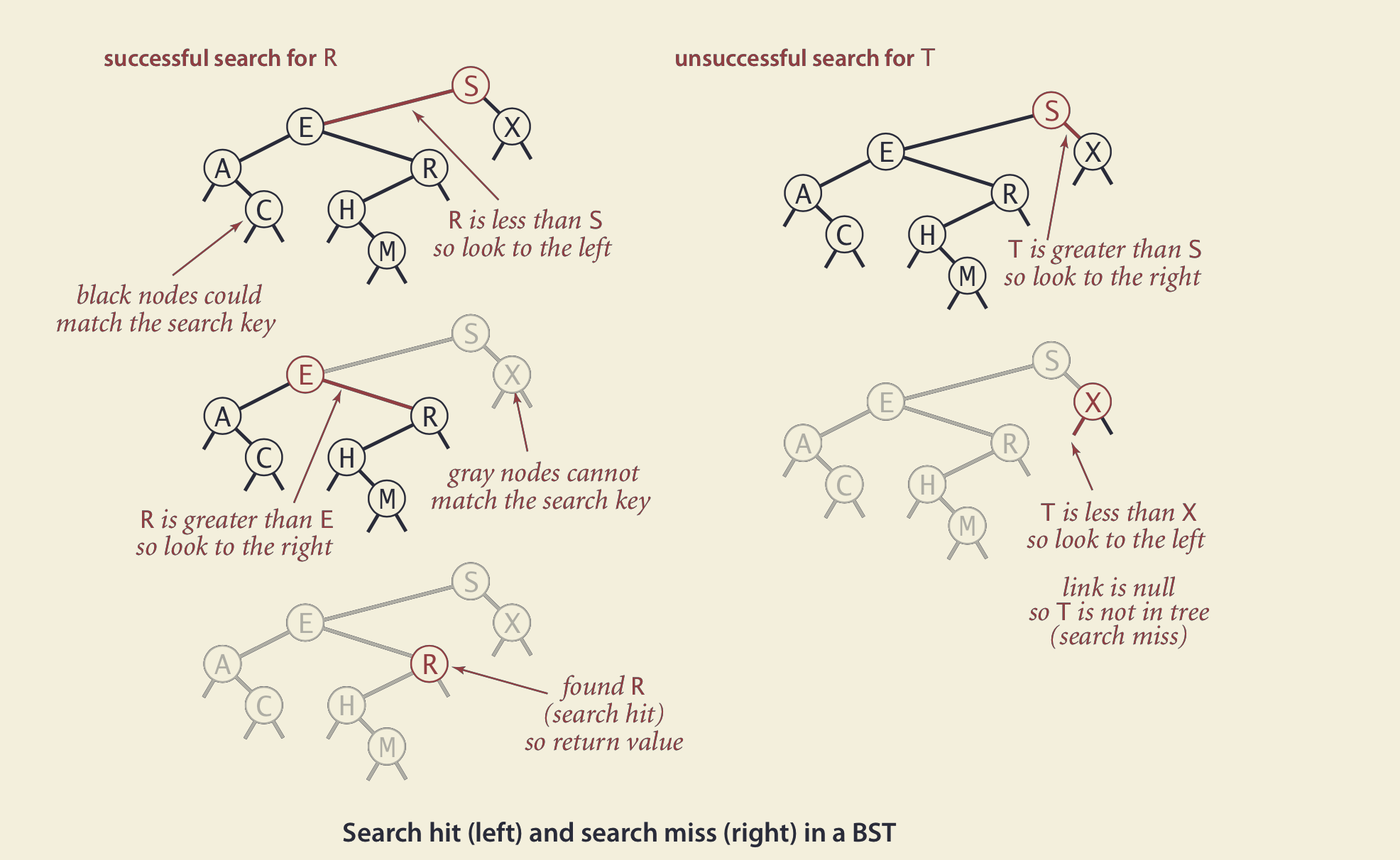
先取根结点，如果根结点的值 等于要查找的值，则返回
如果要查找的值，小于根结点的值，则在根结点的左子树中递归查找；
如果要查找的值，大于根结点的值，则在根结点的右子树中递归查找

Algorithm find

find(value, root){

	if root is empty
		return false

	if value = root.value
		return true

	if value < root.value
		return find(value, root.left)

	else
		return find(value, root.right)
}

*/

type Node struct {
	Val   int
	Left  *Node
	Right *Node
}

func find(value int, root *Node) bool {
	if root == nil {
		return false
	}

	if value == root.Val {
		return true
	}

	if value < root.Val {
		return find(value, root.Left)
	}

	return find(value, root.Right)

}

3.2 插入

/*
二叉查找树的插入操作，与查找过程相似，
首先，从根结点开始，比较根结点的值 和插入的节点的值
如果插入的节点 小于 根结点的值，则递归遍历根结点的左子树，查找插入位置，插入
如果插入的节点 大于 根结点的值，则递归遍历根结点的右子树，查找插入位置，插入

Algorithm: insert a new node and return the root of the update tree

insert(node, root)

if root is empty
	return node

if node.value = root.value
	// do nothing, element already in tree

else if node.value < root.value
	root.left <- insert(node, root.left)

else
	root.right <- insert(node, root.right)

return root

*/

func Insert(node *Node, root *Node) *Node {
	if root == nil {
		return node
	}

	if node.Val == root.Val {
		// do nothing, element already in tree
	}

	if node.Val < root.Val {
		root.Left = Insert(node, root.Left)
	}

	if node.Val > root.Val {
		root.Right = Insert(node, root.Right)
	}

	return root
}

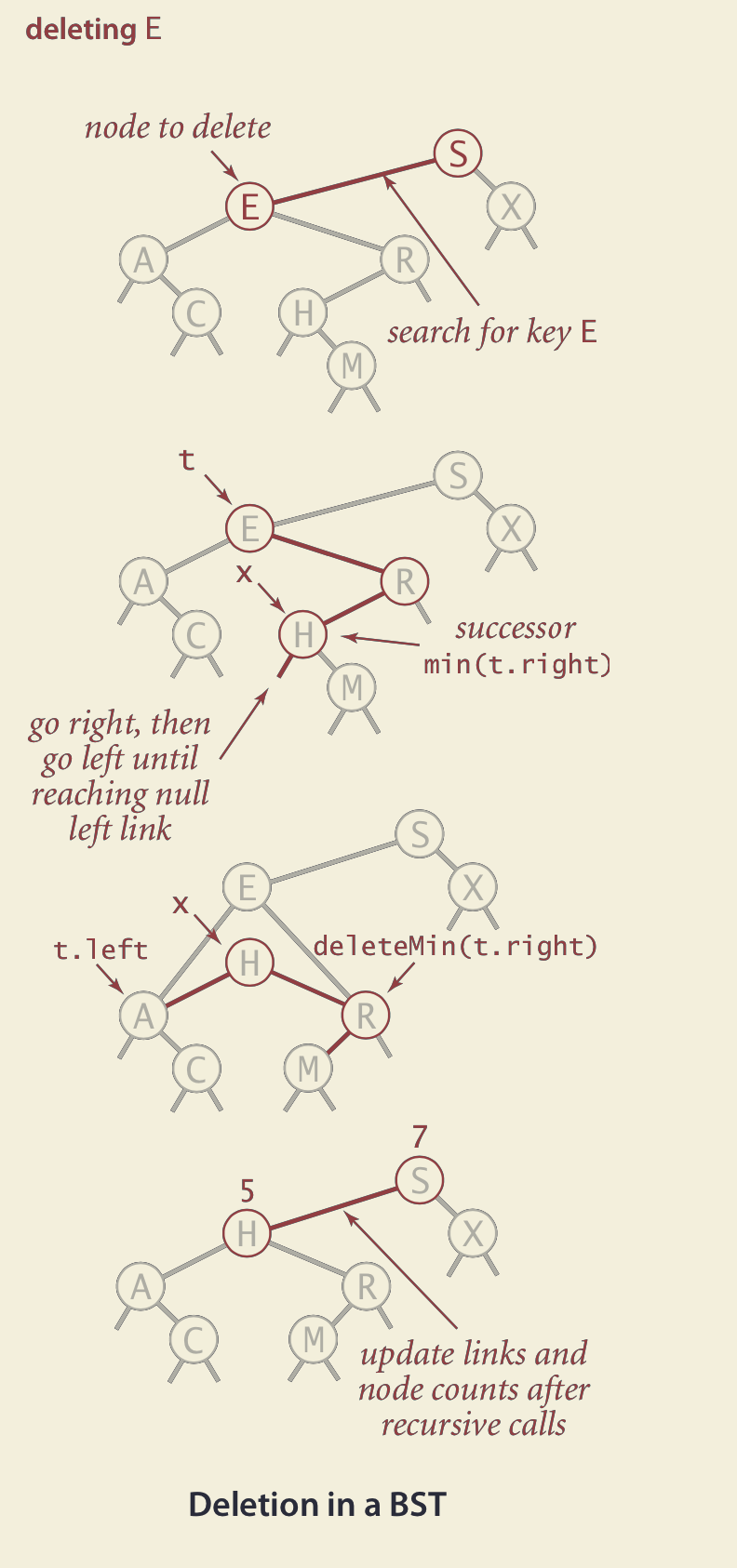
3.3 删除