计算两个经纬度点间的距离
纬度线投射在图上看似水平的平行线,但实际上是不同半径的圆。有相同特定纬度的所有位置都在同一个纬线上。
赤道的纬度为0°,将行星平分为南半球和北半球。
纬度是指某点与地球球心的连线和地球赤道面所成的线面角,其数值在0至90度之间。位于赤道以北的点的纬度叫北纬,记为N,位于赤道以南的点的纬度称南纬,记为S。
纬度数值在0至30度之间的地区称为低纬地区,纬度数值在30至60度之间的地区称为中纬地区,纬度数值在60至90度之间的地区称为高纬地区。
赤道、南回归线、北回归线、南极圈和北极圈是特殊的纬线。
纬度1秒的长度
地球的子午线总长度大约40008km。平均:
纬度1度 = 大约111km
纬度1分 = 大约1.85km
纬度1秒 = 大约30.9m
The haversine formula
在球上任意两个点的距离有如下关系:
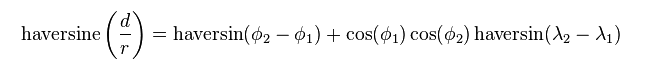

其中,d:两点间距离,既球面距离;
r:球的半径;
 :点1和点2的纬度;
:点1和点2的纬度;
 :点1和点2的经度;
:点1和点2的经度;


Java版:

1 import com.google.android.maps.GeoPoint; 2 3 public class DistanceCalculator { 4 5 private double Radius; 6 7 // R = earth's radius (mean radius = 6,371km) 8 // Constructor 9 DistanceCalculator(double R) { 10 Radius = R; 11 } 12 13 public double CalculationByDistance(GeoPoint StartP, GeoPoint EndP) { 14 double lat1 = StartP.getLatitudeE6()/1E6; 15 double lat2 = EndP.getLatitudeE6()/1E6; 16 double lon1 = StartP.getLongitudeE6()/1E6; 17 double lon2 = EndP.getLongitudeE6()/1E6; 18 double dLat = Math.toRadians(lat2-lat1); 19 double dLon = Math.toRadians(lon2-lon1); 20 double a = Math.sin(dLat/2) * Math.sin(dLat/2) + 21 Math.cos(Math.toRadians(lat1)) * Math.cos(Math.toRadians(lat2)) * 22 Math.sin(dLon/2) * Math.sin(dLon/2); 23 double c = 2 * Math.asin(Math.sqrt(a)); 24 return Radius * c; 25 } 26 }
C#版:

1 using System; 2 namespace HaversineFormula 3 { 4 /// <summary> 5 /// The distance type to return the results in. 6 /// </summary> 7 public enum DistanceType { Miles, Kilometers }; 8 /// <summary> 9 /// Specifies a Latitude / Longitude point. 10 /// </summary> 11 public struct Position 12 { 13 public double Latitude; 14 public double Longitude; 15 } 16 class Haversine 17 { 18 /// <summary> 19 /// Returns the distance in miles or kilometers of any two 20 /// latitude / longitude points. 21 /// </summary> 22 /// <param name=”pos1″></param> 23 /// <param name=”pos2″></param> 24 /// <param name=”type”></param> 25 /// <returns></returns> 26 public double Distance(Position pos1, Position pos2, DistanceType type) 27 { 28 double R = (type == DistanceType.Miles) ? 3960 : 6371; 29 double dLat = this.toRadian(pos2.Latitude - pos1.Latitude); 30 double dLon = this.toRadian(pos2.Longitude - pos1.Longitude); 31 double a = Math.Sin(dLat / 2) * Math.Sin(dLat / 2) + 32 Math.Cos(this.toRadian(pos1.Latitude)) * Math.Cos(this.toRadian(pos2.Latitude)) * 33 Math.Sin(dLon / 2) * Math.Sin(dLon / 2); 34 double c = 2 * Math.Asin(Math.Min(1, Math.Sqrt(a))); 35 double d = R * c; 36 return d; 37 } 38 /// <summary> 39 /// Convert to Radians. 40 /// </summary> 41 /// <param name="val"></param> 42 /// <returns></returns> 43 private double toRadian(double val) 44 { 45 return (Math.PI / 180) * val; 46 } 47 } 48 }

1 Position pos1 = new Position(); 2 pos1.Latitude = 40.7486; 3 pos1.Longitude = -73.9864; 4 Position pos2 = new Position(); 5 pos2.Latitude = 24.7486; 6 pos2.Longitude = -72.9864; 7 Haversine hv = new Haversine(); 8 double result = hv.Distance(pos1, pos2, DistanceType.Kilometers);
JavaScript版:

1 var R = 6371; // km 2 var dLat = (lat2-lat1)*Math.PI/180; 3 var dLon = (lon2-lon1)*Math.PI/180; 4 var a = Math.sin(dLat/2) * Math.sin(dLat/2) + 5 Math.cos(lat1*Math.PI/180) * Math.cos(lat2*Math.PI/180) * 6 Math.sin(dLon/2) * Math.sin(dLon/2); 7 var c = 2 * Math.asin(Math.sqrt(a)); 8 var d = R * c;
Python版:

1 #coding:UTF-8 2 """ 3 Python implementation of Haversine formula 4 Copyright (C) <2009> Bartek Górny <bartek@gorny.edu.pl> 5 6 This program is free software: you can redistribute it and/or modify 7 it under the terms of the GNU General Public License as published by 8 the Free Software Foundation, either version 3 of the License, or 9 (at your option) any later version. 10 11 This program is distributed in the hope that it will be useful, 12 but WITHOUT ANY WARRANTY; without even the implied warranty of 13 MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the 14 GNU General Public License for more details. 15 16 You should have received a copy of the GNU General Public License 17 along with this program. If not, see <http://www.gnu.org/licenses/>. 18 """ 19 20 import math 21 22 def recalculate_coordinate(val, _as=None): 23 """ 24 Accepts a coordinate as a tuple (degree, minutes, seconds) 25 You can give only one of them (e.g. only minutes as a floating point number) and it will be duly 26 recalculated into degrees, minutes and seconds. 27 Return value can be specified as 'deg', 'min' or 'sec'; default return value is a proper coordinate tuple. 28 """ 29 deg, min, sec = val 30 # pass outstanding values from right to left 31 min = (min or 0) + int(sec) / 60 32 sec = sec % 60 33 deg = (deg or 0) + int(min) / 60 34 min = min % 60 35 # pass decimal part from left to right 36 dfrac, dint = math.modf(deg) 37 min = min + dfrac * 60 38 deg = dint 39 mfrac, mint = math.modf(min) 40 sec = sec + mfrac * 60 41 min = mint 42 if _as: 43 sec = sec + min * 60 + deg * 3600 44 if _as == 'sec': return sec 45 if _as == 'min': return sec / 60 46 if _as == 'deg': return sec / 3600 47 return deg, min, sec 48 49 50 def points2distance(start, end): 51 """ 52 Calculate distance (in kilometers) between two points given as (long, latt) pairs 53 based on Haversine formula (http://en.wikipedia.org/wiki/Haversine_formula). 54 Implementation inspired by JavaScript implementation from http://www.movable-type.co.uk/scripts/latlong.html 55 Accepts coordinates as tuples (deg, min, sec), but coordinates can be given in any form - e.g. 56 can specify only minutes: 57 (0, 3133.9333, 0) 58 is interpreted as 59 (52.0, 13.0, 55.998000000008687) 60 which, not accidentally, is the lattitude of Warsaw, Poland. 61 """ 62 start_long = math.radians(recalculate_coordinate(start[0], 'deg')) 63 start_latt = math.radians(recalculate_coordinate(start[1], 'deg')) 64 end_long = math.radians(recalculate_coordinate(end[0], 'deg')) 65 end_latt = math.radians(recalculate_coordinate(end[1], 'deg')) 66 d_latt = end_latt - start_latt 67 d_long = end_long - start_long 68 a = math.sin(d_latt/2)**2 + math.cos(start_latt) * math.cos(end_latt) * math.sin(d_long/2)**2 69 c = 2 * math.asin(math.sqrt(a)) 70 return 6371 * c 71 72 73 if __name__ == '__main__': 74 warsaw = ((21, 0, 30), (52, 13, 56)) 75 cracow = ((19, 56, 18), (50, 3, 41)) 76 print points2distance(warsaw, cracow)
PHP版:

1 function getDistance($latitude1, $longitude1, $latitude2, $longitude2) { 2 $earth_radius = 6371; 3 4 $dLat = deg2rad($latitude2 - $latitude1); 5 $dLon = deg2rad($longitude2 - $longitude1); 6 7 $a = sin($dLat/2) * sin($dLat/2) + cos(deg2rad($latitude1)) * cos(deg2rad($latitude2)) * sin($dLon/2) * sin($dLon/2); 8 $c = 2 * asin(sqrt($a)); 9 $d = $earth_radius * $c; 10 11 return $d; 12 }
参考地址:
http://www.codecodex.com/wiki/Calculate_distance_between_two_points_on_a_globe
http://en.wikipedia.org/wiki/Haversine_formula
