QBXT Day 4 数学，数论

今天讲一讲数论吧（虽然清明讲过了）

进制转换

我们来看10这个数怎么转换成k进制

因为10=2^3+2^1,所以10就是1010

三进制也同理10=3^2+3^0，所以就是101

我们对于一个10进制数，就可以用短除法来求解

比如55的三进制

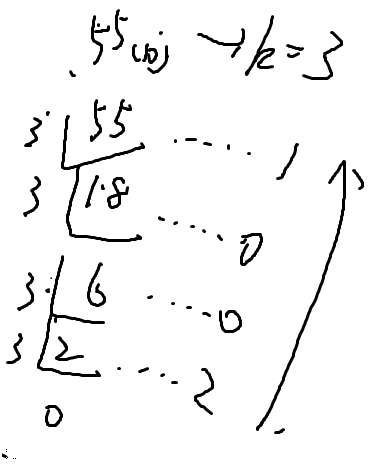
这里我们把所有的余数向上写一遍，其实代码实现的话就直接写一个栈就可以了，还有一个没啥用的注意事项，就是读的问题

怎么把一个k进制数转成十进制的X？

假设我们有一个k进制数X，总共有n位，那么他就是XnXn-1Xn-2......X1X0

我们第i位其实就对应着k^i，我们最后计算就行了

有几种特殊的进制写法，

2进制，我要写二进制1001，那我就写int a=01001（因为正常的数不会前导0）

8进制，

10进制，

16进制，我要写1001，就是0x1001，算一下就是16^3+1=4097

注意，

16进制是0-15，大于9的数字我们用字母代替，所以就是0123456789ABCDEF

高精度

因为我们知道即使是long long也是-2^63~2^63，差不多也就是二十位左右，但是我们有那种好几百位的，就很变态了

所以我们考虑用到高精度

其实就是模拟竖式进行加减法

比如2333+233=2566

 肯定就是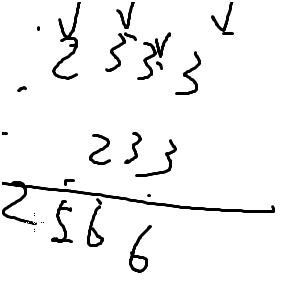

第一个问题，我们怎么把这个数存下来（当然是用字符数组读入然后转成）

正常想法是正着存进去啊

但是肯定是有问题的

 

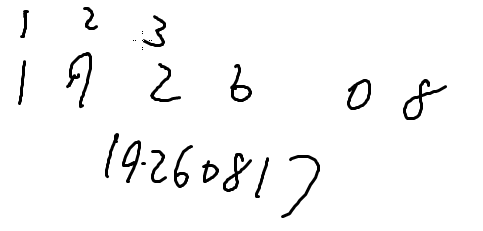
我们存了19260817，但是后来又加了一个123，所以我们高精度存数就是反着存的

也就是存的是71806291我们计算的时候就可以从下标0开始计算了

这样就能保证做加法的时候各位一定是对齐的

因为之前我们学习的这里我们学一个新的高精度写法，

把相关运算符进行重载，也就是说对高精度本身进行构造（其实就相当于手写python的底层高精实现）

就是说因为很多题是不光只有高精度的，所以我们在调试的时候就先开int，当我们过掉小数据就证明我们的思路没有问题，那我们直接把int改成高精类型，把之前的模板贴进去就行了

这里还有一个代码的写法问题，我们之前是面向过程的编程语言，那么现在学一下面向对象的编程语言，这一点在北大的那本算法程序设计有讲到，主要的就是模块化，可修改化的问题

所以我们开一个struct

struct gaojing
{
    int z[2333333];//用来存这个数的数组
    int l;//这个高精度是个l位的数
};

里面有两个值z[]和l分别表示数字本身和长度

但是我们这里有一个坑，struct里面的值是很玄学的，有可能是随机值也有可能全是0

即使我保证初始全是0，他也是错了，为什么？

比如我a=0，那么a.z[xxxx]==0没问题，但是其本身长度是1啊，所以我们得把l改成1

但是我们肯定不能每一个数都给它memest一遍，这样太慢了，所以我们得用一下构造函数

就是说我们每一次构造一个gaojing类型的数的时候，就自动改变他的值，这样就方便很多了

高精度的板子一定要手写，因为它的本质其实就是一个大模拟，而且说句实话数据结构什么的也都是模拟，我们一定要熟练运用

 

我们最好是把这几个运算符都给它编写一下

C++里面有一种特殊的函数叫做重载运算符，是这样写的

数据类型   operator  （你要重载的符号）（你要算的数）

gaojing operator+(gaojing a,gaojing b)
{
    XXXXXXX
    retrun ans;
}

重载运算符对于普通运算是没有问题的，两个数都是gaojing类型的时候，他才会走这个函数，并且返回一个a+b的gaojing类型的值

但是这是有问题的，为什么？（ZHX最喜欢干这种恶心的事情了）

我们看一看另一个代码

gaojing operator + (gaojing &a,gaojing &b) 
{
    bulabulabula
    return ans;
}

括号当中因为加了一个&，所以我们会对于外面的数产生影响

原因是这样的

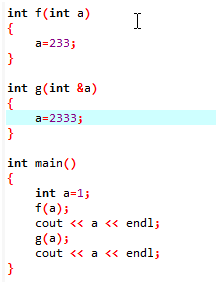
F()在实现的时候，是先把a拷贝一份a’然后传给F()，所以我们怎么改都不会对原型有影响，但是我们在G()实现的时候，直接把a传了过去，而没有备份

再回头看这个代码，我们做这个高精加法运算的时候，如果不加&，所以每一次都要拷贝二十多万位的数组，那这就很刺激啊。。。。。

肯定很多人会认为就已经对了

但是还是错的。。。。。。。因为我们很有可能算出来的答案是对的，但是很有可能把a和b的值改了，这个事情就很玄学啊对吧，所以我们就得在类型前加一个const，来使a不会改变

而且如果想要用STL也就是sort这些对gaojing进行操作的话，你不加&是不行的

 

我们来看代码吧

 

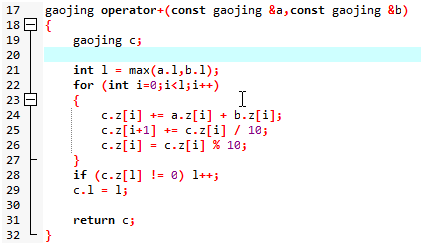
我们看到21行，这里取了两个gaojing数位较长的那个，这个自己想一想也能明白

然后就是正常进行加法，之后取模运算就可以，但是最后有一个很刺激的情况啊，就是说有可能我们两个数相加之和位数会变多一位，所以我们看28行，对最后的实际位数进行运算，这样出来的位数就是正确的了、

我们还得重载一下输入输出

Friend代表有源函数，i代表input，stream代表流，所以istream就是读入流

Static代表静态变量，而且去掉是错的，我们一定要记住，在函数里面一定不要开数组，如果非要开，那也得是加seatic，不然会爆系统栈

然后正常读入就好，最后我们要记住返回cin

 

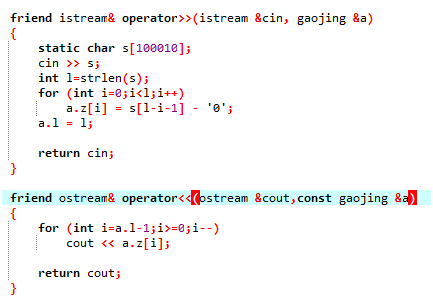
同样的还有Cout，和cin类似吧，但是有一点是要加一个const，这是为了保证我们输出的时候a的值不会变，同样的，最后我们要返回一个cout

再看乘法的代码

 

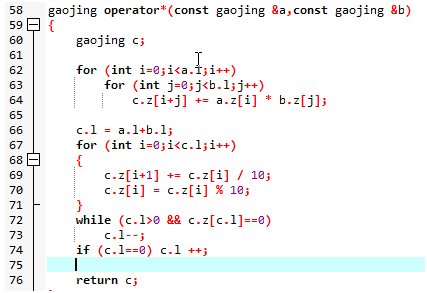
取第一个数的第i位和第二个数的第j位相乘，把答案加到c的第i+j位上，因为一个a位数乘以一个b位数最多是有a+b位，也就是c.l=a.l+b.l

这里就是进位过程

 

但是因为不一定所有的数乘出来最后都会把位数补满，所以我们要检测他到底有多少位

 

终于开始讲数论了

指数定义：

以π（x）表示不超过x的素数的个数，我们可以证明

Lim（x->∞）π（x） ln x/x=1

先是判断素数

for（int i=2；i<=sqrt(n); ++i）
   if（n%i==0)    return false;
return true;

但是有一个问题，这个代码会把所有小于等于1

的数会判为质数，所以我们加一个判断式

再写一下优化就是了

时间复杂度是sqrt（n）（没优化是O(n)）

然后就是求区间的筛法

用刚才那个方法能够得到一个O(n*sqrt(n))的方法，但是太慢了

我们得换个方法，就是说我们把所有的质数的倍数都标记为不是质数，最后剩下的就都是质数了，所以我们转换成代码的话就是这样的

for (int i=2,i<=n;++i)
    for(int j=i+i;j<=n;j+=i)
            prime [j] =false;

这玩意的时间复杂度就是O(nlogn)

 这里的logn是怎么来的呢？其实就是   n/2+n/3+n/4+....+n/n
≈n(1+1/2+1/3+...+1/n)
≈n log n

上面那个式子叫做调和级数

有一个非常经典的民科《调和级数既是收敛的又是发散的》（可以当笑话看）

怎么做优化？
实际上，我们只需要让一个数只被质数筛掉就行

 这就是埃拉托色尼筛法

for(a=2;a<=n;a++)
    if(not_prime[a]=false)
        for(int b=1+1;b<=n;b+=a)
            not_prime[b]=true; 

这样的话我们就做到了只把指数的倍数筛掉的，埃拉托色尼筛法的复杂度是O（Nloglogn）

最后讲一种线性的筛法

我们希望每个数只被筛掉一次，来看代码吧

memset(not_prime,0,sizeof(not_prime));//初始化为都是质数 
not_prime[1]=true;//1不是质数 
for(int i=2;i<=n;i++)
{
    if(!not_prime[i])    prime[++prime_count]=i;
    //如果i还没有被标记为不是质数 ，就把i加到质数表里面
    for(int j=1;j<=prime_count;j++)
    {
        if(prime[j]*i>n) break;//枚举i的质数倍
        not_prime[prime[j]*i]=true;
        if(i%prime[j]==0) break;
        //如果i是第j个质数的倍数，就跳出循环 
        //因为i有prime[j]这个因子，再枚举prime[j]就会变大
        //break掉就可以保证一定是被它的最小质因子筛掉 
     } 
}

我们一开始认为所有的数都是质数，除了1

第三行是如果i是质数，那么把i假如质数表中

第4行开始枚举当前质数表里所有的质数

我们原来的方法是枚举i的任意倍数，但是这里就成了枚举i的质数倍             

其实这里看懂很容易，我们只需要加上一个输出调试，你就能看出来他是怎么筛的了

GCD（最大公因数）

这玩意很好写，用辗转相除法就行

int gcd(int a,int b)
{
    if(b==0) return a;//gcd(a,0)=a
    else return gcd(b,a%b);
}

STL里头有一个自带的函数__gcd(x,y)但是貌似CCF是不让用的

有了GCD我们就能解同余方程

gcd(a,b)=g
==>ax+by=g(x,y∈Z)

如：
gcd(30,12)=6
==>1*30-2*12=6
==>-1*30+3*12=6
显然结果有无数组

已经知道gcd(a,b)=g
求一组ax+by=g解

拓展欧几里得算法：

int exgcd(int a,int b,int &x,int &y)
{
    if(b==0)//到了最底层 
    {
        x=1,y=0;//这是一组解 
        return a;//最大公因数 
    }
    else 
    {
        int g=exgcd(b,a%b,x,y);
        int t=x;
        x=y,y=t-a/b*x;//x'=y,y'=x-y*(a/b)
        return g;
    }
}

还有一个问题就是求逆元，这个是在模一个数意义下来代替除法的，详情还是看数学班的笔记吧