洛谷P1549 棋盘问题（2）

P1549 棋盘问题（2）

题目描述

在N*N的棋盘上（1≤N≤10），填入1，2，…，N*N共N*N个数，使得任意两个相邻的数之和为素数。

例如：当N=2时，有：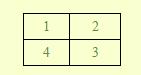

其相邻数的和为素数的有：

1+2，1+4，4+3，2+3

当N=4时，一种可以填写的方案如下：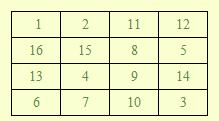

在这里我们约定：左上角的格子里必须填数字1。

输入输出格式

输入格式：

一个数N

输出格式：

如有多种解，则输出第一行、第一列之和为最小的排列方案；若无解，则输出“NO”。

输入输出样例

输入样例#1：

1

输出样例#1：

NO

输入样例#2：

2

输出样例#2：

1 2
4 3

#include<iostream>
#include<cstdio>
using namespace std;
int n,map[11][11],p[210],cnt;
int ok[110][210];
bool th[210],vis[110],flag;
void dfs(int x,int y){
    if(x==n+1){
        flag=1;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                cout<<map[i][j]<<' ';
            }cout<<endl;
        }
    }
    if(flag)return;
    int pre1,pre2;
    if(x==1)pre1=pre2=map[x][y-1];
    else if(y==1)pre1=pre2=map[x-1][y];
    else pre1=map[x-1][y],pre2=map[x][y-1];
    int nxt1=x,nxt2=y+1;
    if(nxt2>n)nxt2=1,nxt1=x+1;
    for(int i=1;i<=ok[pre1][0];i++){
        int now=ok[pre1][i];
        if(!th[now+pre2]&&!vis[now]){
            vis[now]=1;
            map[x][y]=now;
            dfs(nxt1,nxt2);
            vis[now]=0;
        }
    }
}
int main(){
    scanf("%d",&n);
    if(n==1){
        printf("NO");
        return 0;
    }
    th[1]=1;
    for(int i=2;i<=200;i++){
        if(!th[i])p[++cnt]=i;
        for(int j=1;j<=cnt&&i*p[j]<=200;j++){
            th[i*p[j]]=1;
            if(i%p[j]==0)break;
        }
    }
    for(int i=1;i<=n*n;i++)
        for(int j=1;j<=cnt;j++){
            int to=p[j]-i;
            if(to>n*n)break;
            if(to>0)ok[i][++ok[i][0]]=to;
        }
    vis[1]=1;
    map[1][1]=1;
    dfs(1,2);
    if(flag==0){
        printf("NO");
        return 0;
    }
} 

#include <iostream>

using namespace std;

int main(){
    int n;
    cin >> n;
    if(n == 2) cout << "1 2" << endl << "4 3";
    else if(n == 4) cout << "1 2 11 12" << endl << "4 15 8 5" <<  endl <<  "7 16 3 14" << endl << "6 13 10 9";
    else if(n == 5) cout << "1 2 3 4 7" << endl << "6 5 14 15 16" << endl << "13 24 23 8 21" << endl << "10 19 18 11 20" << endl << "9 22 25 12 17";
    else cout << "NO";
    return 0;
}