十大基本排序算法
排序算法是《数据结构与算法》中最基本的算法之一。
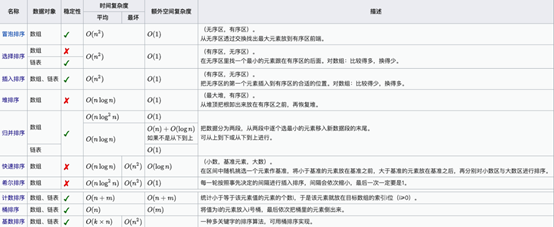
排序算法可以分为内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。常见的内部排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。这里使用python实现这十大排序算法。
一、冒泡排序
算法步骤
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
# 冒泡排序 def bubbleSort(arr): for i in range(1, len(arr)): for j in range(0, len(arr)-i): if arr[j] > arr[j+1]: arr[j], arr[j + 1] = arr[j + 1], arr[j] return arr
二、选择排序
算法步骤
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
#选择排序 def selectionSort(arr): for i in range(len(arr) - 1): # 记录最小数的索引 minIndex = i for j in range(i + 1, len(arr)): if arr[j] < arr[minIndex]: minIndex = j # i 不是最小数时,将 i 和最小数进行交换 if i != minIndex: arr[i], arr[minIndex] = arr[minIndex], arr[i] return arr
三、插入排序
算法步骤
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
# 插入排序 def insertionSort(arr): for i in range(len(arr)): preIndex = i-1 current = arr[i] while preIndex >= 0 and arr[preIndex] > current: arr[preIndex+1] = arr[preIndex] preIndex-=1 arr[preIndex+1] = current return arr
四、希尔排序
算法步骤
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
按增量序列个数 k,对序列进行 k 趟排序;
每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
# 希尔排序 def shellSort(arr): import math gap=1 while(gap < len(arr)/3): gap = gap*3+1 while gap > 0: for i in range(gap,len(arr)): temp = arr[i] j = i-gap while j >=0 and arr[j] > temp: arr[j+gap]=arr[j] j-=gap arr[j+gap] = temp gap = math.floor(gap/3) return arr
五、归并排序
算法步骤
1.申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
2.设定两个指针,最初位置分别为两个已经排序序列的起始位置;
3.比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
4.重复步骤 3 直到某一指针达到序列尾;
5.将另一序列剩下的所有元素直接复制到合并序列尾。
#归并排序 def mergeSort(arr): import math if(len(arr)<2): return arr middle = math.floor(len(arr)/2) left, right = arr[0:middle], arr[middle:] return merge(mergeSort(left), mergeSort(right)) def merge(left,right): result = [] while left and right: if left[0] <= right[0]: result.append(left.pop(0)) else: result.append(right.pop(0)); while left: result.append(left.pop(0)) while right: result.append(right.pop(0)); return result
六、快速排序
算法步骤
1.从数列中挑出一个元素,称为 "基准"(pivot);
2.重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
3.递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
#快速排序 def quickSort(arr, left=None, right=None): left = 0 if not isinstance(left,(int, float)) else left right = len(arr)-1 if not isinstance(right,(int, float)) else right if left < right: partitionIndex = partition(arr, left, right) quickSort(arr, left, partitionIndex-1) quickSort(arr, partitionIndex+1, right) return arr def partition(arr, left, right): pivot = left index = pivot+1 i = index while i <= right: if arr[i] < arr[pivot]: swap(arr, i, index) index+=1 i+=1 swap(arr,pivot,index-1) return index-1 def swap(arr, i, j): arr[i], arr[j] = arr[j], arr[i]
七、堆排序
算法步骤
1.创建一个堆 H[0……n-1];
2.把堆首(最大值)和堆尾互换;
3.把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
4.重复步骤 2,直到堆的尺寸为 1。
#堆排序 def buildMaxHeap(arr): import math for i in range(math.floor(len(arr)/2),-1,-1): heapify(arr,i) def heapify(arr, i): left = 2*i+1 right = 2*i+2 largest = i if left < arrLen and arr[left] > arr[largest]: largest = left if right < arrLen and arr[right] > arr[largest]: largest = right if largest != i: swap(arr, i, largest) heapify(arr, largest) def swap(arr, i, j): arr[i], arr[j] = arr[j], arr[i] def heapSort(arr): global arrLen arrLen = len(arr) buildMaxHeap(arr) for i in range(len(arr)-1,0,-1): swap(arr,0,i) arrLen -=1 heapify(arr, 0) return arr
八、计数排序
算法步骤
1.找出待排序的数组中最大和最小的元素
2.统计数组中每个值为i的元素出现的次数,存入数组C的第i项
3.对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
4.反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
#计数排序 def countingSort(arr, maxValue): bucketLen = maxValue+1 bucket = [0]*bucketLen sortedIndex =0 arrLen = len(arr) for i in range(arrLen): if not bucket[arr[i]]: bucket[arr[i]]=0 bucket[arr[i]]+=1 for j in range(bucketLen): while bucket[j]>0: arr[sortedIndex] = j sortedIndex+=1 bucket[j]-=1 return arr
九、桶排序
算法步骤
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:
- 在额外空间充足的情况下,尽量增大桶的数量
- 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
def bucketSort(arr): # 选择一个最大的数 max_num = max(nums) # 创建一个元素全是0的列表, 当做桶 bucket = [0]*(max_num+1) # 把所有元素放入桶中, 即把对应元素个数加一 for i in nums: bucket[i] += 1 # 存储排序好的元素 sort_arr = [] # 取出桶中的元素 for j in range(len(bucket)): if bucket[j] != 0: for y in range(bucket[j]): sort_nums.append(j) return sort_arr
十、基数排序
算法步骤
先排元素的最后一位,再排倒数第二位,直到所有位数都排完
#基数排序 def radix_sort(s): i = 0 # 记录当前正在排拿一位,最低位为1 max_num = max(s) # 最大值 j = len(str(max_num)) # 记录最大值的位数 while i < j: bucket_list =[[] for _ in range(10)] #初始化桶数组 for x in s: bucket_list[int(x / (10**i)) % 10].append(x) # 找到位置放入桶数组 print(bucket_list) s.clear() for x in bucket_list: # 放回原序列 for y in x: s.append(y) i += 1
在学习python实现基础算法时,在GitHub上找到一个使用python实现算法可视化,作者是真的厉害,有兴趣的可以去看下。
这里附上链接:https://github.com/ZQPei/Sorting_Visualization