matlab练习程序（扩展曲线边界）

这里有这样一个问题，比如我们有一条曲线，要求出曲线的左右一定范围的边界。

方法是：

1. 取曲线前后帧局部点对，计算点对得到的直线方程L1。

2. 点法式计算垂直于L1的直线L2。

3. 根据拓展半径d以点对中后一个点画圆，计算圆和L2的交点。

4. 连接所有交点得到曲线的边界。 

matlab代码如下：

clear all;
close all;
clc;

d=10;

t = 1:0.1:20;
x = 80*t - 5*t.*sin(t) ;
y = t.^2 + cos(t);

plot(x,y)
hold on;

line1=[];
line2=[];
for i=2:length(t)
    
    k = (y(i)-y(i-1))/(x(i)-x(i-1));
    
    k1 = -1/k;
    b1 = y(i)-k1*x(i);
    
    tmp = sqrt(-b1^2 + d^2 + d^2*k1^2 - 2*b1*k1*x(i) - k1^2*x(i)^2 + 2*b1*y(i) + 2*k1*x(i)*y(i) - y(i)^2);
    
    x1 = (-b1*k1 + x(i) + k1*y(i) - tmp)/(1 + k1^2);
    y1 = b1 - (b1*k1^2)/(1 + k1^2) + (k1*x(i))/(1 + k1^2) + (k1^2*y(i))/(1 + k1^2) - (k1*tmp)/(1 + k1^2);
    
    x2 = (-b1*k1 + x(i) + k1*y(i) + tmp)/(1 + k1^2);
    y2 = b1 - (b1*k1^2)/(1 + k1^2) + (k1*x(i))/(1 + k1^2) + (k1^2*y(i))/(1 + k1^2) + (k1*tmp)/(1 + k1^2);
    
    line1=[line1;x1 y1];
    line2=[line2;x2 y2];
end
plot(line1(:,1),line1(:,2),'r');
plot(line2(:,1),line2(:,2),'r');

axis equal

结果如下：

半径10米的结果：

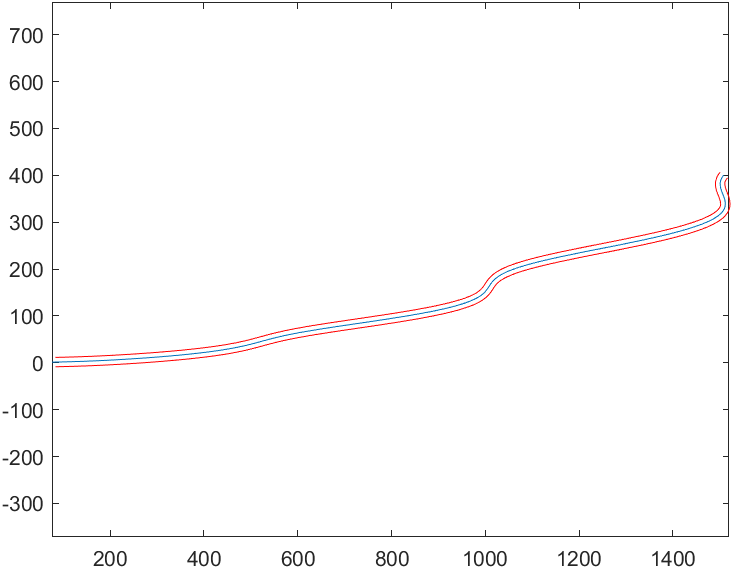
半径50米的结果：

可以看出半径大的时候在曲线曲率大的地方会形成毛刺，要解决毛刺问题其实可以先求得中心曲线的方程，再用上述方法得到边界离散点，最后用最小二乘以曲线的模型对离散点进行拟合。

应该就可以解决毛刺了，我这里就不实验了，应该是可以的。