计算方法:
1. 两条直线方向向量v1和v2的叉积,得到平行于两条直线的平面v3。
2. 计算v3与第一条直线v1叉积,得到垂直于v3并且过线v1的平面v4,计算面v4与线v2的交点,得到线v2上的点t2。
3. 计算v3与第二条直线v2叉积,得到垂直于v3并且过线v2的平面v5,计算面v5与线v1的交点,得到线v1上的点t1。
4. t1与t2即为异面直线最近点,t1与t2距离即为异面直线距离。
matlab代码如下:
clear all;close all;clc; p1 = rand(3,1)*2-1; %随机生成一条直线 v1 = rand(3,1)*2-1; p2 = rand(3,1)*2-1; %随机生成另一条直线 v2 = rand(3,1)*2-1; v1 = v1/norm(v1); v2 = v2/norm(v2); t = -1:0.01:1; X1 = v1.* repmat(t,3,1) + p1; X2 = v2.* repmat(t,3,1) + p2; v3 = cross(v1,v2); %计算和两条直线都平行的平面 v3 = v3/norm(v3); [planx,plany] = meshgrid(min([X1(1,:) X2(1,:)]):0.02:max([X1(1,:) X2(1,:)]),min([X1(2,:) X2(2,:)]):0.01:max([X1(2,:) X2(2,:)])); %生成平行平面 planz1 = p1(3) -(v3(1)*(planx-p1(1))+v3(2)*(plany-p1(2))) / v3(3); planz2 = p2(3) -(v3(1)*(planx-p2(1))+v3(2)*(plany-p2(2))) / v3(3); t1 = (cross(v3,v2)'*(p2-p1))/(cross(v3,v2)'*v1)*v1 + p1; %计算过一条直线和v3面垂直的面,计算得到另一条直线和该面的交点。 t2 = (cross(v3,v1)'*(p1-p2))/(cross(v3,v1)'*v2)*v2 + p2; %和上一步类似 mesh(planx,plany,planz1); %画出平行平面 hold on; mesh(planx,plany,planz2); plot3(X1(1,:),X1(2,:),X1(3,:),'b'); %画出两条直线 plot3(X2(1,:),X2(2,:),X2(3,:),'r'); plot3(t1(1),t1(2),t1(3),'b*'); %画出最近点 plot3(t2(1),t2(2),t2(3),'r*'); plot3([t1(1) t2(1)],[t1(2) t2(2)],[t1(3) t2(3)],'g'); %画出最短线段 grid on; axis equal;
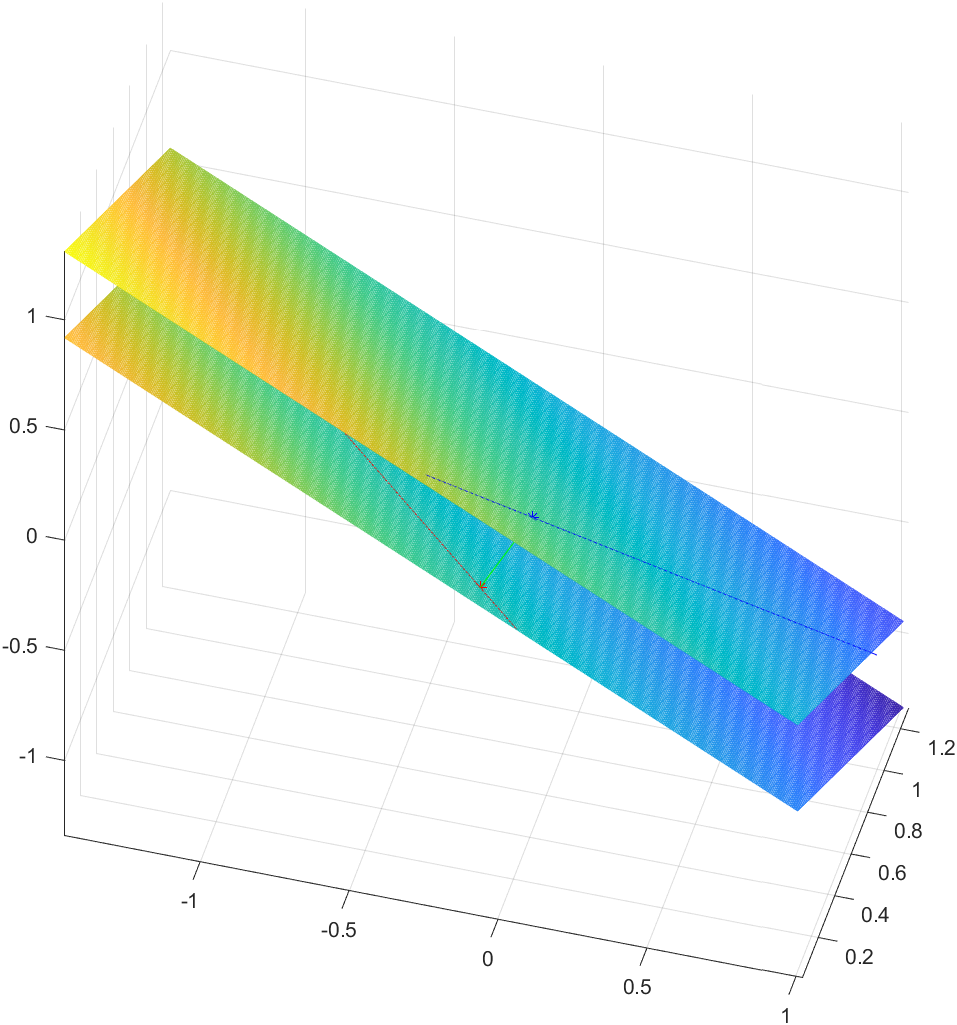
结果如下: