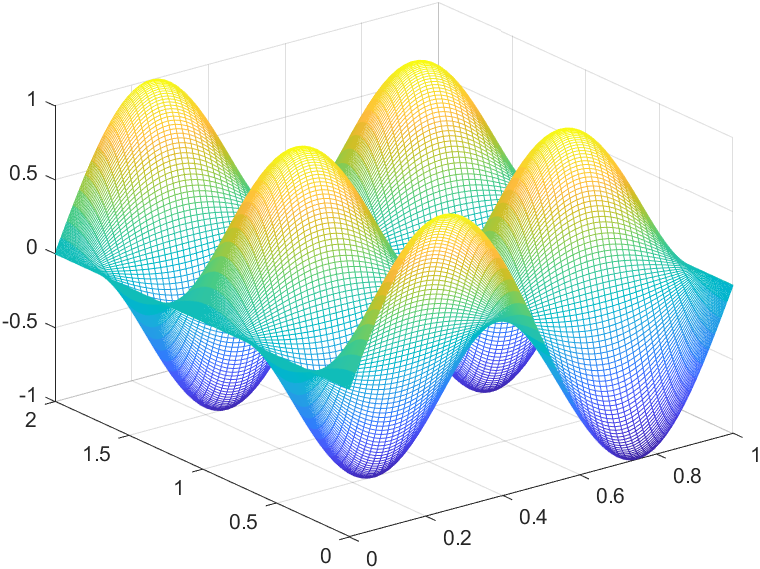
上一篇实现了二维热传导方程数值解,这里我们计算波动方程数值解。
波动方程是一种双曲型偏微分方程。
这里依然用差分法计算。
一维波动方程如下:

写成差分形式:
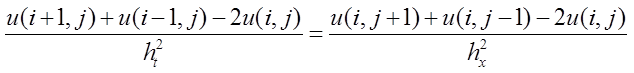 整理一下就能得到u(i+1,j)。
整理一下就能得到u(i+1,j)。
matlab代码如下:
clear all;close all;clc; t = 2; %时间范围,计算到2秒 x = 1; %空间范围,0-1米 m = 320; %时间方向分320个格子 n = 64; %空间方向分64个格子 ht = t/(m-1); %时间步长dt hx = x/(n-1); %空间步长dx u = zeros(m,n); %设置边界条件 i=2:n-1; xx = (i-1)*x/(n-1); u(1,2:n-1) = sin(2*pi*xx); u(2,2:n-1) = sin(2*pi*xx); %根据推导的差分公式计算 for i=2:m-1 for j=2:n-1 u(i+1,j) = ht^2*(u(i,j+1)+u(i,j-1)-2*u(i,j))/hx^2 + 2*u(i,j)-u(i-1,j); end end %画出数值解 [x1,t1] = meshgrid(0:hx:x,0:ht:t); mesh(x1,t1,u)
结果如下: