matlab练习程序（Prim最小生成树）

算法步骤：

1.任意找一顶点加入树中。

2.寻找所有与树相邻的元素，并取其边权重最小的并且不在树中的元素入树。

3.继续第二步，直到所有元素都入树。

效果和Kruskal算法是类似的。

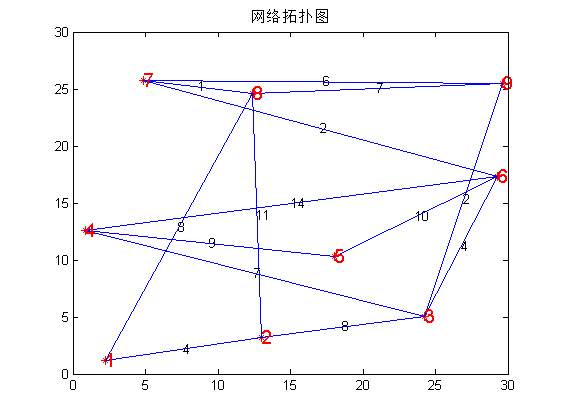
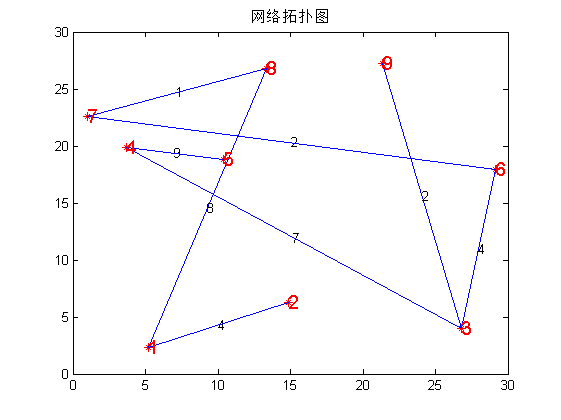
matlab代码：

main.m

clear all;
close all;
clc;

G=[0 4 0 0 0 0 0 8 0;
   4 0 8 0 0 0 0 11 0;
   0 8 0 7 0 4 0 0 2;
   0 0 7 0 9 14 0 0 0;
   0 0 0 9 0 10 0 0 0;
   0 0 4 14 10 0 2 0 0;
   0 0 0 0 0 2 0 1 6;
   8 11 0 0 0 0 1 0 7;
   0 0 2 0 0 0 6 7 0];

[m n]=size(G);

q=[1];      %已经被标记的元素
k=1;        %已经标记的元素个数
A=[];       %最后产生的最小生成树
while length(q)~=m
    e=[];
    for i=1:k
        for j=1:n
            if G(q(i),j)~=0 && ~biaoji(j,q) %不在数中的元素
                e=[e;G(q(i),j) q(i) j];
            end
        end
    end
    
    [junk index]=min(e(:,1));    %求与当前标记的所有元素相邻的权重最小的边的索引
    A=[A;e(index,:)];       %最小生成树的三元组表示
    q=[q e(index,3)];
    k=k+1;  
end

biaoji.m

function re=biaoji(j,biao)  %判断j点是否已被标记
    l=length(biao);
    for i=1:l
       if j==biao(i) 
            re=1;
            return;
       end
    end
    re=0;
    return;
end