分类算法的评价

一、分类算法评价指标

1.分类准确度的问题

分类算法如果用分类准确度来衡量好坏将会存在问题。例如一个癌症预测系统，输入体检信息，可以判断是否有癌症，预测准确度可以达到99.9%，看起来预测系统还可以，但是如果癌症的产生概率只有0.1%，那么系统只要预测所有人都是健康的就可以达到99.9%的准确率，因此虽然准确率很高，但是预测系统实际上没有发挥什么作用。更加极端的如果癌症概率只有0.01%，那么预测所有人都是健康的概率是99.99%，比预测系统的结果还要好。因此可以得到结论：在存在极度偏斜的数据中，应用分类准确度来评价分类算法的好坏是远远不够的。

2.混淆矩阵

对于二分类问题。可以得到如下的混淆矩阵。

通过混淆矩阵可以得到精准率和召回率，用这两个指标评价分类算法将会有更好的效果。

3.精准率和召回率

精准率：分类正确的正样本个数占分类器判定为正样本的样本个数的比例（预测分类为1，相应的预测对的概率）。

　　　　对应于检索中的查准率，检索出相关文档数/检索出的文档总数

之所以使用1的分类来计算精准率是因为，在实际生活中，1代表着受关注的对象，例如：癌症预测系统中，1就代表着患癌症，40%意味着，系统做出100次病人患有癌症的预测结论，其中有40%结论是准确的。

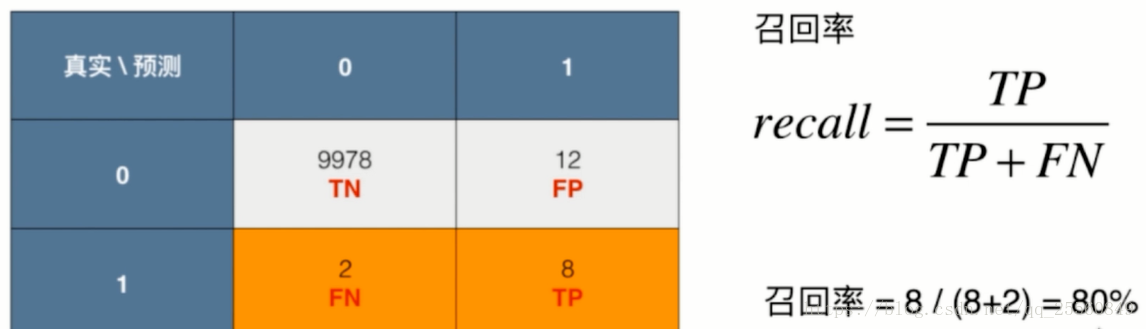
召回率：分类正确的正样本个数占真正的正样本个数的比例（真实分类为1，相应的预测对的概率）。

　　　　对应于检索中的查全率。检索出相关文档数/文档库中相关文档总数

召回率意味着如果有10个癌症患者，将会有8个被预测到。

 

区别精确率和召回率主要记住他们是分母不同就好了，召回率是对应测试集中的正类数据而言，而准确率是对应预测结果为正类的数据而言。

另一种图解：

现在假设有10000个人，预测所有的人都是健康的，假设有10个患病，则有如下的混淆矩阵：

对于准确率：9990/10000=99.9%。对于精准率：0/0没有意义。对于召回率：0/10=0。可以看出模型对于预测疾病其实并不好。

4.代码实现

4.1 自己编写代码动手实现以下精准率与召回率：

采用digits数据集，为了达到极度偏斜的效果，我们将所有数据设为如果是9为1，不是9为0

import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target.copy() #如果直接引用那么y变了，target也会变
y[digits.target==9] = 1
y[digits.target!=9] = 0

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
# 逻辑回归预测一哈
from sklearn.linear_model import LogisticRegression 
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
log_reg.score(X_test, y_test)

y_log_predict = log_reg.predict(X_test) # 获取预测的答案

def TN(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 0) & (y_predict == 0))

def FP(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 0) & (y_predict == 1))

def FN(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 1) & (y_predict == 0))


def TP(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 1) & (y_predict == 1))


def confusion_matrix(y_true, y_predict):
    return np.array([
        [TN(y_true, y_predict), FP(y_true, y_predict)],
        [FN(y_true, y_predict), TP(y_true, y_predict)]
    ])

confusion_matrix(y_test, y_log_predict)

def precision_score(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fp = FP(y_true, y_predict)
    try:
        return tp / (tp + fp)
    except:
        return 0.0

def recall_score(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fn = FN(y_true, y_predict)
    try:
        return tp / (tp + fn)
    except:
        return 0.0
print("score:" , log_reg.score(X_test, y_test))
print("precision_score", precision_score(y_test, y_log_predict))
print("recall_score", recall_score(y_test, y_log_predict))

 结果：

score: 0.9755555555555555
precision_score 0.9473684210526315
recall_score 0.8

4.2 sklearn代码实现

由于计算逻辑比较简单，所以直接给出sklearn中封装好的实现。

#因为是与指标相关，所以都是metrics
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test,y_log_predict)
from sklearn.metrics import precision_score #sklearn中的精准率
precision_score(y_test,y_log_predict)
from sklearn.metrics import recall_score    #sklearn中的召回率
recall_score(y_test,y_log_predict)

 结果：0.8

5.对精准率和召回率的分析

对于一个模型得到了精准率和召回率，那么应该如何通过这两个指标对模型进行评价，又或者是一个模型经过调参后，得到不同的精准率和召回率，应该选取哪个参数对应的精准率和召回率才好。这个需要根据不同的场景进行选择。

例如：对于股票预测，更多的应该是关注精准率，假设关注股票上升的情况，高精准率意味着TP值高（正确地预测到股票会升），这个时候可以帮助人们调整投资，增加收入，如果这一指标低，就以为FP值高（错误地认为股票会升），也就是说股票其实是降的，而预测成升了，这将会使用户亏钱。而召回率低只是意味着在股票上升的情况中，对几个股票上升的情况没有被预测到，这对于投资者来说也是可以接受的，毕竟没有亏钱，因此低召回率对用户影响不是很大。

例如：对于疾病预测领域，更多的应该关注召回率，因为高召回率意味着能够更多地将得病的病人预测出来，这个对于患病者非常重要。而精准率低意味着错误地预测病人患病，而这个时候只要被预测患病的人再去检查一下即可，实际上是可以接受的，因此低精准率对用户影响不大。

而某些情况可能需要同时考虑到两个指标，以达到一个均衡。这个时候就需要F1 score。这个称为精准率和召回率的调和平均值。可以发现只有两个值都比较高的时候，F1才会比较高。如果两个值某一个很高，另一个很低，F1值也不会高。

from sklearn.metrics import f1_score
f1_score(y_test,y_log_predict)

二、精准率和召回率

精准率和召回率之间是互相矛盾的，如果提高召回率，精准率就不可避免的下降，如果精准率提高，召回率就不可避免的下降。

分类阈值的取值的影响

在逻辑回归中，我们让决策边界是 θ* X = 0作为决策边界，即大于0的分类1，小于0的分类0，我们可以不让他是0，而是一个常数threshold.下图是threshold取不同的值可能产生的变化

如图所示，五角星为1，圆形为0。划的竖线代表决策边界。可以看到，当精准率提高时，召回率就下降，当召回率提高时，精准率就下降，二者是个矛盾。

log_reg.decision_function(X_test)[:10]
# 这个函数就是逻辑回归模型里那个threshold的值，模型的默认值都是0
'''调用函数输出结果
array([-22.05700185, -33.02943631, -16.21335414, -80.37912074,
       -48.25121102, -24.54004847, -44.39161228, -25.0429358 ,
        -0.97827574, -19.71740779])'''
np.min(decision_scores) #分类标准阈值的最大值
np.max(decision_scores)
y_predict_2 = np.array(decision_scores >= 5, dtype='int') #这样就改变了分类标准的阈值，大于5的才是1

Precision-Recall-Curve(PR曲线)

随着分类阈值的不断变化，precision和recall值也会不断变化，那么我们可以画出其相应的曲线，可以在曲线中找到一个F1 Score最高的分类阈值。通常在recall要急剧下降的那个位置。

实现自己的PR曲线

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()
y[digits.target==9] = 1
y[digits.target!=9] = 0

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
decision_scores = log_reg.decision_function(X_test)

from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
precisions = [] 
recalls = []
thresholds = np.arange(np.min(decision_scores), np.max(decision_scores), 0.1) #以0.1为步长获取分类阈值最大值到最小值里的点
for threshold in thresholds:
    y_predict = np.array(decision_scores >= threshold, dtype='int') # 每个点求一次 precision_score和recall_score
    precisions.append(precision_score(y_test, y_predict))
    recalls.append(recall_score(y_test, y_predict))
#画出对应的值
plt.plot(thresholds,precisions,label="precision")
plt.plot(thresholds,recalls,label="recall")
plt.legend()
plt.show()

 

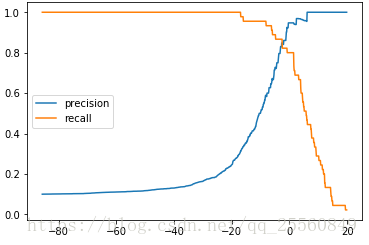
绘制precision和recall曲线。

plt.plot(precisions,recalls)
plt.show() #快速下降的点，可能就是比较平衡的点

 

scikit-learn 中的PR曲线

from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_test, decision_scores)
#注意通过这个函数得到的precision和recall的最后一个值分别为1和0，没有对应的Score
plt.plot(thresholds, precisions[:-1])  #所以不取最后一个
plt.plot(thresholds, recalls[:-1])
plt.show()


plt.plot(precisions, recalls)
plt.show()

 

 注意：

ROC曲线

ROC曲线是用来描述TPR与FPR之间的曲线之间的关系.

TPR（True-Positive-Rate）: 代表预测为1并且预测对了的样本数量占真实值为1的百分比为多少

FPR（False-Positive-Rate）：代表预测为1但预测错了的样本数量占真实值为0的百分比是多少

 

分类阈值改变，TPR和FPR的变化：

可以看到FPR和TPR呈现相一致的关系，这个也容易理解。当召回率提高时，说明会尽量将1样本都包含进去（竖线左移），而这个时候就会增加错分的0样本（更多的0被包含进去），因此TN减小，FP增大，必然导致FPR的增大。

会发现当阈值变低，TPR与FPR值都变高，阈值变低那么预测值更容易变成1，所以预测值为1的样本也多了，真实值为1的总量是不变的,所以TPR变高，同理预测错了的样本也会变多。

代码实现 FPR 和 TPR，并绘制 ROC 曲线：

　　封装：

def TPR(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fn = FN(y_true, y_predict)
    try:
        return tp / (tp + fn)
    except:
        return 0.

def FPR(y_true, y_predict):
    fp = FP(y_true, y_predict)
    tn = TN(y_true, y_predict)
    try:
        return fp / (fp + tn)
    except:
        return 0.

 　　求 TPR 和 FPR：

import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()
y[digits.target==9] = 1
y[digits.target!=9] = 0

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
decision_scores = log_reg.decision_function(X_test)


from playML.metrics import FPR, TPR

fprs = []
tprs = []
thresholds = np.arange(np.min(decision_scores), np.max(decision_scores), 0.1)

for threshold in thresholds:
    # dtype=‘int‘：将数据类型从 bool 型转为 int 型；
    y_predict = np.array(decision_scores >= threshold, dtype=‘int‘)
    fprs.append(FPR(y_test, y_predict))
    tprs.append(TPR(y_test, y_predict))

　　绘制 ROC 曲线：

import matplotlib.pyplot as plt
plt.plot(fprs, tprs)
plt.show()

 

• 分析：

1. ROC 曲线与图形边界围成的面积，作为衡量模型优劣的标准，面积越大，模型越优；
2. 可以是同样算法不同超参数所得的不同模型，也可以是不同算法所得的不同模型。

scikit-learn中的ROC曲线：

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
decision_scores = log_reg.decision_function(X_test) #获取逻辑回归每个样本的decision_scores

from sklearn.metrics import roc_curve
fprs, tprs, thresholds = roc_curve(y_test, decision_scores) #获取tpr与fpr的值

plt.plot(fprs, tprs)
plt.show()

 

ROC曲线的面积越大，那么我们的模型就越好，因为如果绘制一个FPR-TPR的曲线，在同样的FPR（犯错率）之下，TPR的值越高，模型越好，相应的它的面积越大。

• 计算 ROC 曲线与坐标轴围成的面积：称 ROC 的 auc；

• 面积越大，模型越优；

from sklearn.metrics import roc_auc_score #求面积， 面积最大就为1，因为TPR与FPR最大值都为1
roc_auc_score(y_test, decision_scores)# 结果：0.98304526748971188

这个将会得到比较高的值，说明auc对于有偏数据并不是很敏感，auc一般用于比较两个模型之间的好坏。

ROC对有偏数据并不敏感，主要用来比较两个模型谁更好一些，比如一个算法不同参数，或者两个不同的算法，都可以用这个来比较，如果他们的数据不是极度偏移的话。

三、多分类评价

1.多分类问题中的混淆矩阵

这里只研究多分类混淆矩阵，其他的以后在详细研究一下。

import numpy as np
import matplotlib.pyplot as plt

from sklearn import datasets
digits = datasets.load_digits() 
X = digits.data #数据并没有进行切割，所以这是10分类问题
y = digits.target

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.8, random_state=666)

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
log_reg.score(X_test, y_test)

y_predict = log_reg.predict(X_test)

from sklearn.metrics import precision_score
precision_score(y_test, y_predict) #如果直接获取矩阵，会报错

 ValueError: Target is multiclass but average='binary'. Please choose another average setting.

precision_score(y_test, y_predict, average="micro") #根据错误提示，需要更改参数
#为了求出多分类的精准度和召回率，必须传入参数average='micro'
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_predict) #跟2分类的混淆矩阵的含义一样，行代表真实值列代表预测值

 结果：

array([[147,   0,   1,   0,   0,   1,   0,   0,   0,   0],
       [  0, 123,   1,   2,   0,   0,   0,   3,   4,  10],
       [  0,   0, 134,   1,   0,   0,   0,   0,   1,   0],
       [  0,   0,   0, 138,   0,   5,   0,   1,   5,   0],
       [  2,   5,   0,   0, 139,   0,   0,   3,   0,   1],
       [  1,   3,   1,   0,   0, 146,   0,   0,   1,   0],
       [  0,   2,   0,   0,   0,   1, 131,   0,   2,   0],
       [  0,   0,   0,   1,   0,   0,   0, 132,   1,   2],
       [  1,   9,   2,   3,   2,   4,   0,   0, 115,   4],
       [  0,   1,   0,   5,   0,   3,   0,   2,   2, 134]], dtype=int64)

其中对角线的代表该分类预测正确的数量，其他位置的值代表预测错误所对应的值。为了直观，现在绘制出图像。

cfm = confusion_matrix(y_test, y_predict)
plt.matshow(cfm, cmap=plt.cm.gray) #一个矩阵的绘制参数，第一个参数是矩阵，第二个参数是颜色
plt.show()

 

from sklearn.metrics import confusion_matrix
cfm = confusion_matrix(y_test,y_predict)
row_sums = np.sum(cfm,axis=1)#将每行相加，得到每行的样本总数
err_matrix = cfm/row_sums#绘制比例
np.fill_diagonal(err_matrix,0)# 因为对角线肯定对的多，将对角线的元素全部置为0
plt.matshow(err_matrix,cmap=plt.cm.gray) #越亮代表值越大，也就是错分的越多
plt.show()#这样就看出把什么看成什么的错误多了