把数字翻译成字符串

题目

　　给定一个数字，按照如下规则翻译成字符串：0翻译成“a”，1翻译成“b”...25翻译成“z”。一个数字有多种翻译可能，例如12258一共有5种，分别是bccfi，bwfi，bczi，mcfi，mzi。实现一个函数，用来计算一个数字有多少种不同的翻译方法。

思路

自上而下，从最大的问题开始，递归 ：

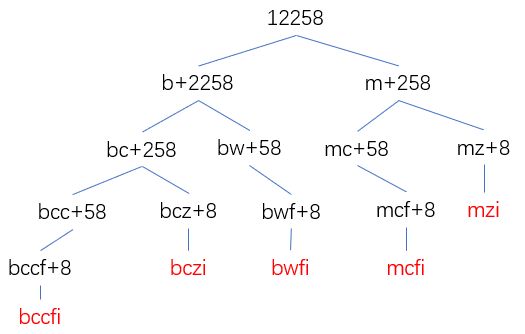
有很多子问题被多次计算，比如258被翻译成几种这个子问题就被计算了两次。

从以上的分析，我们可以看出，这个问题可以拆分成多个子问题来求解，并且子问题有重叠部分，状态转移方程如下：

      f(i-1)+f(i-2), 10<=c(i-1,i)<=25
f(i)=
      f(i-1), otherwise

其中，f(i) 表示数字从左往右第 i 个的翻译种数，c(i-1, i) 表示数字从左往右第 i - 1 和第 i 个字符拼接后的数字（例如：12258 的 c(1, 2)=22）。

#include <iostream>
#include <vector> 
using namespace std;

class Solution
{
    public:
        int translation_count(const int num);
};
int Solution::translation_count(const int num)
{
    if(num<0)
        return 0;
    
    string num_of_str=to_string(num);
    int len=num_of_str.length();
    vector<int> v(len,0);
    int count=0;
    
    for(int i=len-1;i>=0;--i)
    {
        if(i<len-1)
            count=v[i+1];//count记录前一位的count值 
        else
            count=1;
        
        if(i<len-1)
        {
            int digit1=num_of_str[i]-'0';
            int digit2=num_of_str[i+1]-'0';
            if(digit1*10+digit2>=10&&digit1*10+digit2<=25)
            {
                if(i<len-2)//当前位与当前位的前一位当成一位数字来算，所以cont要加i+2的值 
                    count+=v[i+2];
                else
                    count+=1;
            }
        }
        v[i]=count;
    }
    return v[0];
}
int main()
{
    int n;
    cin>>n;
    
    Solution s;
    cout<<s.translation_count(n)<<endl;
    return 0;
}