串的应用与kmp算法讲解
1. 写作目的
平时学习总结的学习笔记,方便自己理解加深印象。同时希望可以帮到正在学习这方面知识的同学,可以相互学习。新手上路请多关照,如果问题还请不吝赐教。
----------2. 串的逻辑存储
串指的是字符串,是一种特殊的线性表,特殊性在于只能存储字符,即可以使用顺序存储也可以使用链式存储,简单的谈一下两种存储结构的优缺点。
顺序存储
顺序存储使用的是数组,既然是数组就是申请固定空间,当串需要拼接,替换时,可能会对数组进行扩容,这种操作就比较耗时,而且有时数组空间利用率很低,也浪费了一部分空间。但是优点也是显而易见的,定位速度快。
链式存储
链式存储不拘束于空间大小,需要多少空间就链上多少个节点。但是如果每个节点都只存一个字符,那么无疑是浪费了空间,如果存多个字符,那么在字符查找上需要花费更多的时间,而且链表本身查找速度慢。
我的观点
更倾向于顺序存储,毕竟字符串更为频繁的操作是查找功能,相较于链式存储,牺牲一点空间,换取更快查询的速度。
3. 串的应用--暴力查找
下面说说串的应用:子串的查找。这个应该很熟悉,有好多应用场景是希望在一个主串中找到子串。可能想找到子串的位置,也可能想判断是否存在,或者替换,全部替换等,这就需要我们能完成最基本的操作,找出子串。
下面这个例子可能是我们最容易想到的算法,直接找:两个循环嵌套,外层循环(i)逐一遍历主串每个字符,判断是否能和子串首字母匹配,如果匹配就继续判断第二个字符,直到把子串遍历完,就是找到了。但是如果中途某个字符不匹配,就把 i 回溯,回到匹配最初的地方,来进行下一个字符的首字母匹配。基本过程如下:
`public static int matchPattern(String origin,String aim) {
char[] origins = origin.toCharArray();
char[] aims = aim.toCharArray();
for(int i = 0; i < origins.length; i++) {
int j = 0,k = i;
for( ; j < aims.length;k++,j++ ) {
if(origins[k] != aims[j]) {
break;
}
}
if(j == aims.length) {
return i - j;
}
}
return -1;
}`
这个方法应该都可以想到,但是这样写会有问题。问题就是:
1.
2.
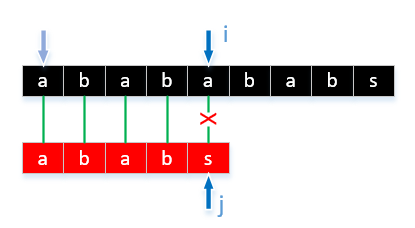
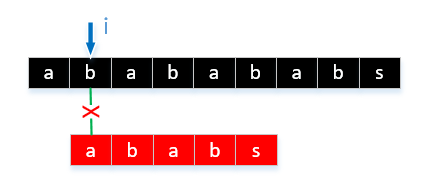
3.
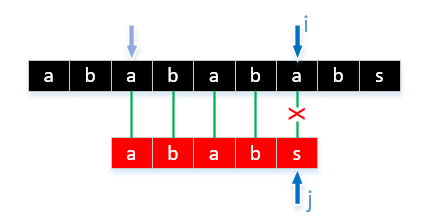
4.
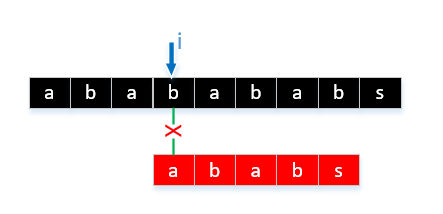
5.
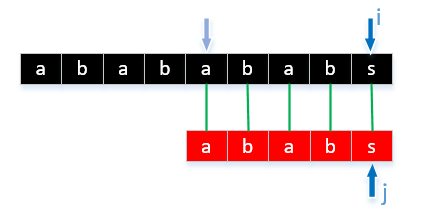
似乎感觉很正常,但如果仔细查看会发现,每当快要匹配成功的时候,因为一个字符的不匹配,就要回头再来,如果字符串很长,而目标字符相似度很高,就会一直重复这样的比较,重要的是其实我们可以根据已知的比较结果来减少比较的次数,来优化这种算法。
4. KMP算法
简单说一下这个算法的背景,KMP的由来。
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称KMP算法)。
用我自己的话概述就是在匹配字符串过程中,因为某个字符匹配失败后,根据已有匹配成功的串推算出下次子串需要移动的位置,从而达到减少不必要匹配次数,实现快速匹配。那么重点就来了,如何推算出子串需要移动的位置? 我怎么知道这样移动后能一定能保证不会有遗漏。那下面我们就一起来分析一下(还是使用上面的例子,为了描述方便,我们把主串称为o(origin),子串称为a(aim) )。
-
第一步这样匹配没问题。
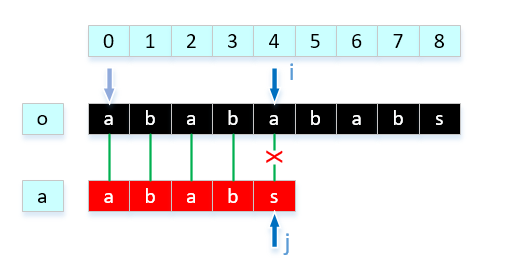
-
第二步这样匹配就出现问题了。 问题是上一步 i 已经移动到 4(数组下标),就因为o[4] != a[4],本次匹配失败,i 需要回溯到 1,j 需要回溯到 0 ,之前的匹配结果信息根本没有派上用场。
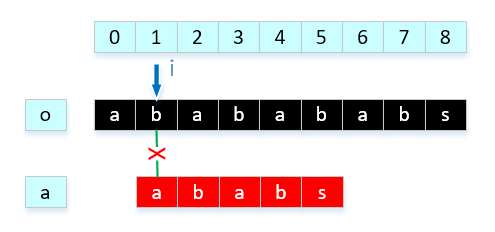
因为根据已经匹配信息,o[0] = a[0],o[1] = a[1],o[2] = a[2],o[3] = a[3],前4位是对应相等的,而且o[2] = a[0],o[3] = a[1],我们完全可以这样移动:
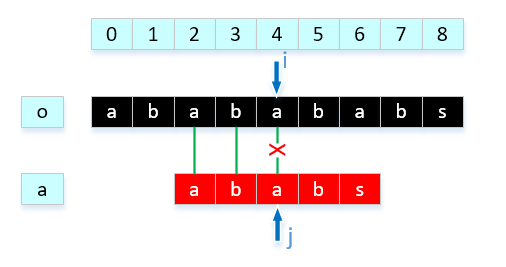
这样的话可以不用比较o[1]与a[0],o[2]与a[0],o[3]与a[1],直接比较o[4]与a[2],省去了不必要的步骤。那么我们继续往下分析,显然o[4] != a[2],因为o[2] = a[0],o[3] = a[1],而且a[0],a[1]不相等,我们可以推断出,o[3] != a[0],所以这一比较步骤也可以省略,直接比较a[4]与a[0]。最终得到结果
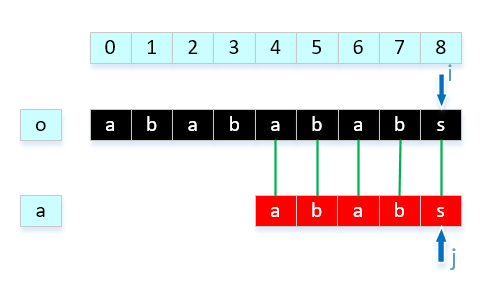
这样的比较方式,是我们可以接受的,根据已知匹配信息省略了许多比较操作,提高效率。 -
那可能有人就要问了,你是怎么知道确切的移动位置,可以让 j 定位到合适的位置,这也就引出了KMP算法的核心的部分,求next[]。next[]有什么作用,next[0],next[1]....next[n]的含义是什么?next是存放对应子串字符冲突后,需要移动 j 的位置。举个例子:next[4] = 2,意思是在 j = 4的位置上子串和主串不匹配,那么主串 i 不需要回溯,直接把 j 回溯到 2,进行比较,也就是把next[]的每个值都求出来,我们就可以轻松准确的更改 j 的位置。了解了next[]的用途,下面我们来学习next[]是如何求出来的。
-
拿之前的例子作为说明:

o[4]与a[4]冲突,前4位对应相等(首要条件),我们要是想根据前4位相等来推算位置,应该会出现2中情况。一:子串前4位互不相等(a[0],a[1],a[2],a[3]没有一个相同的),根据以上2个条件(o,a对应相等),直接可以推算,a[0]下次应该直接和o[4]比,原因就是a[0]不会和o前4位任意字符相等。 二:子串前4位有字符相等,而且是前后缀对应相等,也是可以推算位置。 插播一下前后缀知识。
例如一串字符 "abadaba"
前缀:{"a","ab","aba","abad","abada","abadab"}
后缀:{"a","ba","aba","daba","adaba","badaba"}
那么前后缀最长匹配相等串"adaba"。
回到刚才的问题,对于串"abab",最长匹配相等串为"ab"。那么我们是可以这样理解的:
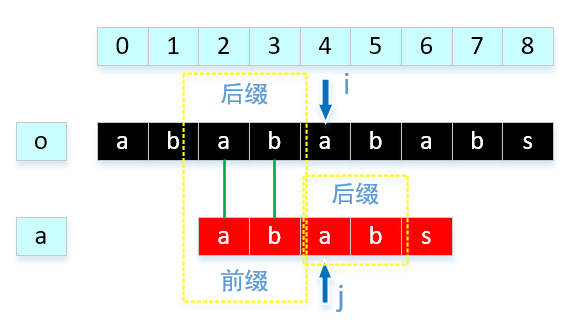
我们分析的是a的前后缀关系,但前提提交是o,a对应位置相等,所以a的前缀就对应了o的后缀,这样我们可以直接移动 j 2的位置。理论基本就这些,我们通过代码来实现一下:public static int[] getNext(String aim,int length) { char[] chars = aim.toCharArray(); int i = 0,j = -1; //next数组长度和aim长度是相等的,因为每一个字符比较出冲突都需要有对应j的位置 int[] next = new int[length]; //第0个位置前是没有前后缀的,所以next[0]我们规定为 -1. next[0] = -1; //第1个位置不匹配,前面只有一个字符,我们只能把j移动到0. next[1] = 0; //注意:这里 i < length -1,而非是 i < length。原因就是 i在循环内部先++,再赋值,如果是 < length会数组越界。 while(i < length-1) { //判断如果对应字符相等,就累加前后缀相同字符长度 if( j == -1 || chars[i] == chars[j] ) { next[++i] = ++j; }else { //注意:就这一句话,困扰我了2天,也许2是比较菜,不过我在文章中,重点解释一下,见文章。 j = next[j]; } } return next; }
重点来了
我们在求解next的时候并不需要o,只需要a就可以得出。我们只需要找出a中前后缀匹配长度,即可。那么我们的方法就是让a和a自己比较。比较的过程如下:
- a[0]与a[1]比较,不相等
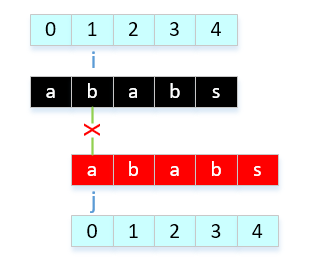
- a[0]与a[2]比较,相等,next[ ++i ] = ++j, next[3] = 1。 意思是什么呢? 可以这样理解,在第3个字符前面的字符中,前后缀最大公共长度为1,也就是有1个公共字符,"a"。那么我知道这个信息有什么用处呢?用处就是当j在3位置上匹配失败,直接改变j为1来继续比较。
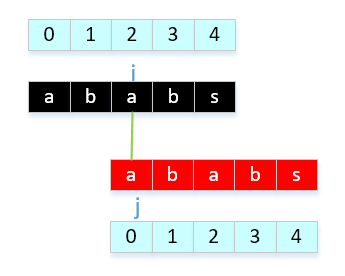
- a[1]与a[3]比较,相等
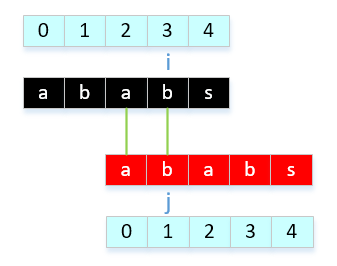
- a[2]与a[4]比较,不相等
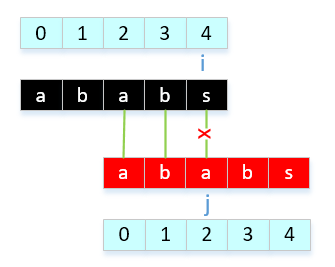
因为只是a[2]与a[4]不等,我们还不能确定具体的公共长度(next[4]的值),接下来我们需要回溯比较,a[4]与a[1],然后a[4]与a[0],如果这样比较多话,就又成了普通的暴力比较 ,我们可以根据已有的结果来推算。下面我来说一下困惑我2天的问题,j = next[ j ]
现有我们已经推算的结果:next[ 0 ] = -1, next[ 1 ] = 0, next[ 2 ] = 0, next[ 3 ] = 1,next[ 4 ] = 2。按照算法来说,就是, j = next[2],j = 0。
我之前一直认为 next[j] 的值代表的就是 j 需要移动的下标,所以很是不能理解把next[4]的值有放到next[]中(怎么能把下标放入到next[]中),也就是next[next[4]],next[4]很清晰的说明是当 j = 4 的位置有字符冲突时,把 j 移动到next[4],也就是2,那next[2]又是啥意思? 也就是实在搞不懂next[next[4]]。2天总是想着这个事,也继续在网上查阅资料,看有没有人和我同样有这个疑问。最后在不断的浏览中,感觉有可以说通的答案了,next[j] 也表示 0 ~ j-1 字符中前后缀最大长度,那么当next[4]失配后,next[4] = 2, 我们知道前面的4个字符,最大公共前后缀长度为2,那么next[2]就是在前2个字符当中再寻找最大前后缀公共的长度,因为是自身和自身比较,公共前后缀字符"ab"和 i=2 时前面的字符是一样的,所以在公共前后缀中再找相同前后缀即为在 i = 2之前找,也就是next[2]的值,相信到这里已经对这个疑问得到解答了。
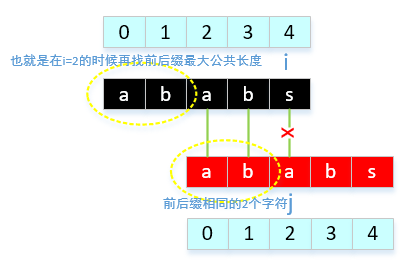
next[ ]的求解我认为是kmp的核心,这个了解完之后,所剩内容不多。引用代码来使用next[ ]完成主串与模式串的查找吧。稍微改动了暴力求解的代码。
public static int kmp(String origin,String aim) {
char[] origins = origin.toCharArray();
char[] aims = aim.toCharArray();
int[] next = getNext(aim,aim.length());
for(int i = 0; i < origins.length; i++) {
int j=0;
for( ; j < aims.length; ) {
if(origins[i] != aims[j]) {
//改动
if(j == 0) {
break;
}
j = next[j];
}else {
i++;
j++;
}
}
if(j == aims.length) {
return i-j;
}
}
return -1;
}
5. 聊一下kmp的改进方案:
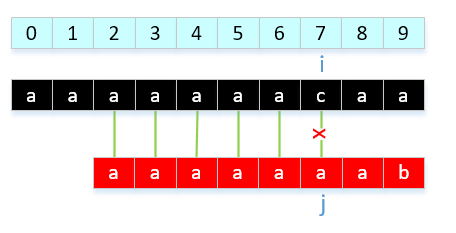
举例说明,有一种情况,我们的next[ ]有待优化,是这样一种情况。模式串:"aaaaaaab",显然我们的结果是next[]{0,0,1,2,3,4,5,6}。当和我们的主串"aaaaaaacaa....",会导致以下情况:
1.
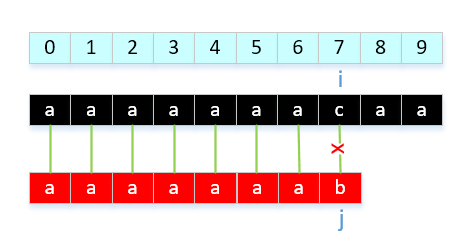
2.

3.
4.
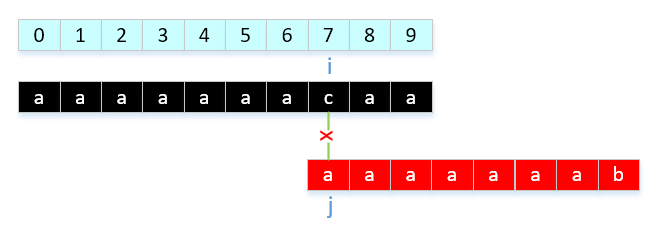
那我们如何改进呢?就是发现模式串中出现连续相等字符就让nextVal[ i ] = nextInt[ j ],解释一下就是: 回溯到上一个字符需要回溯的位置,因为2组前后缀对应想等,那就和上一个做相同处理。
public static int[] getNextVal(String aim,int length) {
char[] chars = aim.toCharArray();
int i = 0,j = -1;
//next数组长度和aim长度是相等的,因为每一个字符比较出冲突都需要有对应j的位置
int[] nextVal = new int[length];
//第0个位置前是没有前后缀的,所以next[0]我们规定为 -1.
nextVal[0] = 0;
//第1个位置不匹配,前面只有一个字符,我们只能把j移动到0.
nextVal[1] = 0;
//注意:这里 i < length -1,而非是 i < length。原因就是 i在循环内部先++,再赋值,如果是 < length会数组越界。
while(i < length-1) {
//判断如果对应字符相等,就累加前后缀相同字符长度
if( j == -1 || chars[i] == chars[j] ) {
i++;
j++;
//相较于getNext()改动的地方
if(chars[i] == chars[j]) { // i == j, i+1 == j+1
nextVal[i] = nextVal[j];
}else {
nextVal[i] = j;
}
}else {
//注意:就这一句话,困扰我了2天,也许是比较菜,不过我在文章中,重点解释一下,见文章。
j = nextVal[j];
}
}
return nextVal;
}
参考文档:
《大话数据结构》