二叉排序树,又称为二叉查找树。它或者是一棵空树,或者具有下列性质:
1.若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值
2.若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值
3.它的左、右子树也分别为二叉排序树
简言而之:中序遍历就一定会得到从小到大排列的序列!
查找操作:
首先看图,假如查找元素为14的数据。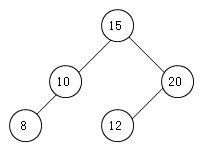
书本采用判断的方式:
else if(key<T->data) return search(T->left,key,T,p); else return search(T->right,key,T,p);
根据移动,(其实为一条单线的移动),最后移动到[12]这个结点位置,12依然小于14,将T->right传入,已经为空所以返回。但此时,f是指向12这个结点的。于是,p=f,则p指向12这个结点最终返回!
完整的查找代码:(这段代码最巧妙的地方在于使用f来跟综)
int search(Tree &T,int key,Tree f,Tree p) { if(!T)/*最后一步,依然没有找到数据*/ { p=f; return FALSE; } else if(key==T->data) { p=T;
return TRUE; } else if(key<T->data) { return search(T->left,key,T,p); } else return search(T->right,key,T,p); }
概括这段代码的意思:
1.如果找到数据,p就指向这个数据
2.如果找不到数据,经过f的辅助,p指向最后一个数据,(更准确的说:不管如何移动,最后必定到达叶子结点!)
插入操作:
经过这么一查找,对于插入操作变的简单了。假如要插入14这个数据,先经过查找,看树中是否有14这个数据,如果有就返回,如果没有就准备插入。
int insert(Tree &T,int key) { Tree p,s; if(!search(T,key,NULL,p))/*如果没有key这个数据*/ { s=(Tree)malloc(sizeof(Node)); s->data=key; s->left=s->right=NULL; if(!p) { T=s; } else if(key<p->data) { p->left=s; } else if(key>p->data) { p->right=s; } return TRUE; } return FALSE; }
经过查找计算,p最终指向叶子结点12,由于>12,所以插入到12结点的右儿子的位置上。
/*------二叉排序树的查找、插入操作------*/ #include <iostream> using namespace std; #define TRUE 1 #define FALSE 0 typedef struct node { int data; struct node *left,*right; }*Tree,Node; int Search(Tree &T,int key,Tree f,Tree &p)/*查找*/ { if(!T)/*最后一步依然没有找到等于key的数据*/ { p=f;/*f必定是叶子结点*/ return FALSE; } else if(key==T->data) { p=T;/*指向等于key的数据*/ cout<<"f->data="<<f->data<<endl; return TRUE; } else if(key<T->data) { return Search(T->left,key,T,p); } else return Search(T->right,key,T,p); } int Insert(Tree &T,int key)/*插入*/ { Tree p,s; if(!Search(T,key,NULL,p))/*如果没有key这个数据*/ { s=(Tree)malloc(sizeof(Node)); s->data=key; s->left=s->right=NULL; if(!p)/*如果是棵空树*/ { T=s;/*s就为根结点*/ } else if(key<p->data) { p->left=s; } else if(key>p->data) { p->right=s; } return TRUE; } return FALSE; } void Traverse(Tree &T)/*遍历*/ { if(T) { Traverse(T->left); cout<<T->data<<" "; Traverse(T->right); } } int main() { Tree T=NULL; int a[]={5,6,7,2,4,10}; for(int i=0;i<sizeof(a)/sizeof(a[0]);i++) Insert(T,a[i]); Traverse(T); return 0; }