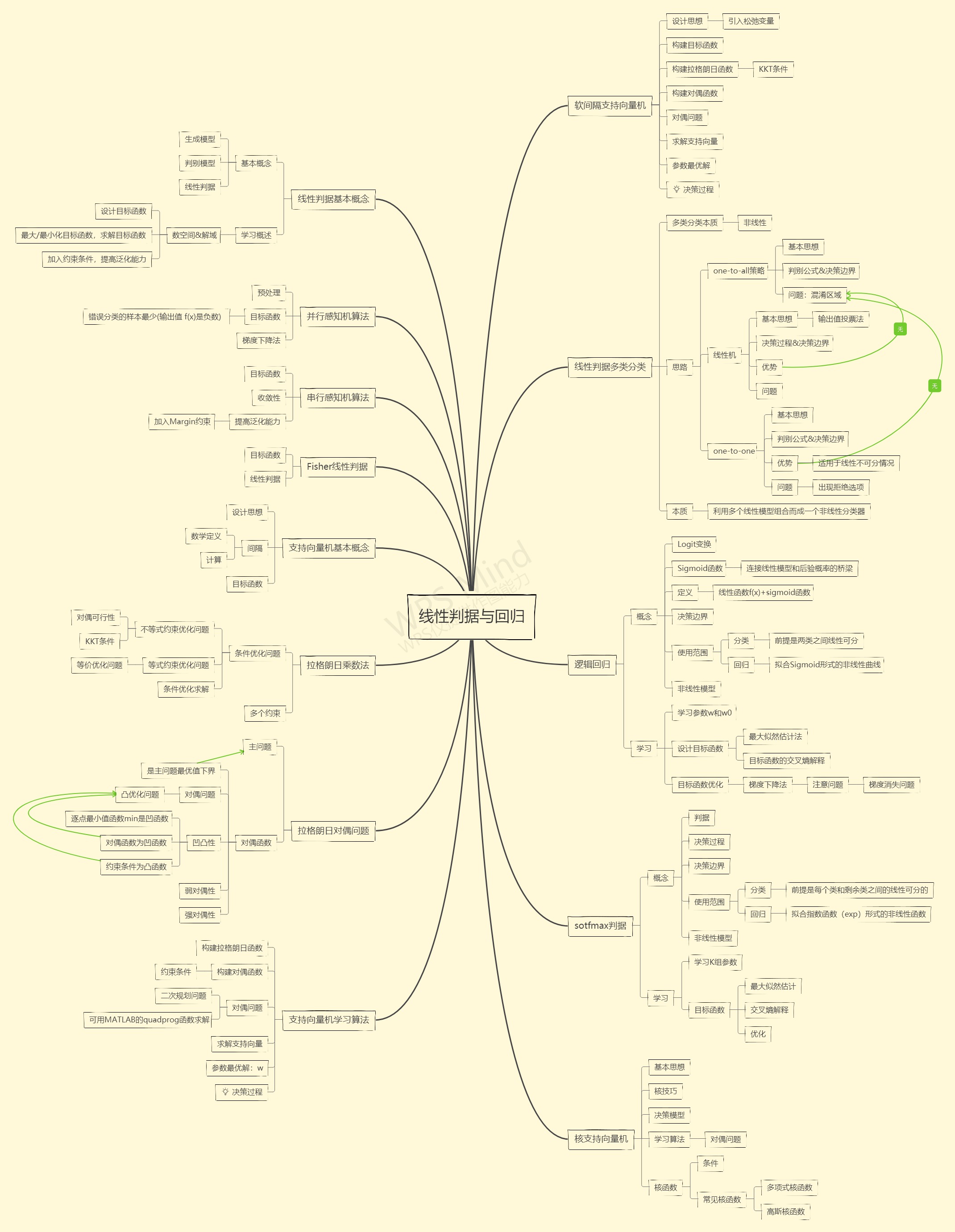
4.1线性判据基本概念
- 生成模型——直接在输入空间中学习其概率密度p(x),
- 对于贝叶斯分类,用作观测似然。然后可以通过这个p(x)生成新的样本数据;也可以检测出较低概率的数据,进行离群点检测。p(x)需要大量的数据才能学习得好,否则出现维度灾难。
- 判别模型——直接在输入空间输出后验概率。快速,省去了观测似然的部分。
- 线性判据——如果判别模型f(x)是线性函数,那f(x)为线性判据。对于二分类,决策边界是线性;对于多分类,相邻两类的决策边界也是线性。计算量少,适合样本少的情况。

4.2线性判据学习概述
参数空间&解域(从解域中找到最优解);
- 设计目标函数 ,
- 最大/最小化目标函数,求解目标函数
- 加入约束条件,提高泛化能力
4.3并行感知机算法
- 预处理

- 目标函数——被错误分类的样本最少(输出值 f(x)是负数)。
- 梯度下降法——使用当前梯度迭代更新参数
4.4 串行感知机算法
- 目标函数

- 感知机:收敛性——如果训练样本是线性可分的,感知机算法理论上收敛于一个解。
- 步长决定收敛的速度、以及是否收敛到局部或者全局最优点
- 提高感知机的泛化能力——加入Margin约束
4.5 Fisher线性判据
- 目标函数

- 线性判据

4.6 支持向量机基本概念
- 目标函数


4.7 拉格朗日乘数法
- 常用于解决条件优化问题
- 条件优化问题——不等式约束优化问题、等式约束优化问题、条件优化求解
- 不等式约束
- 极值点落在可行区域内 ——直接通过
 获得极值点
获得极值点 - 极值点落在可行域边界
- 极值点落在可行区域内 ——直接通过
- KKT条件

4.8 拉格朗日对偶问题
- 对偶函数

- 对偶函数是主问题的最优值下界
- 对偶函数是凹函数
- 对偶问题是凸优化问题;对偶问题的极值是唯一的全局极值点
- 弱对偶性、强对偶性


4.9 支持向量机学习算法
构建拉格朗日函数、构建对偶函数、求解对偶问题(可用MATLAB提供的quadprog函数求解)、求解支持向量、参数最优解
- 识别决策

4.10 间隔支持向量机
- 目标函数

- 构建拉格朗日函数、构建对偶函数、求解对偶问题、求解支持向量、参数最优解
- 决策过程

4.11 线性判据多类分类
- 多类分类本质——非线性
- 思路一:One-to-all策略
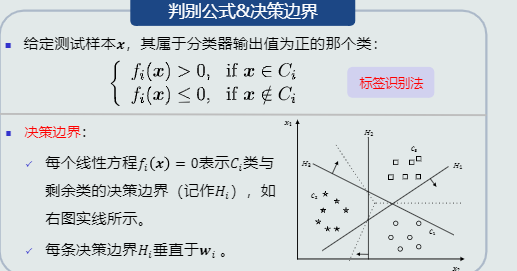
- 思路二:线性机
- 基于one-to-all策略训练k个线性分类器,每个分类器对应一个类
- 决策使用输出值投票法
- 决策过程

- 思路三:One-to-one策略
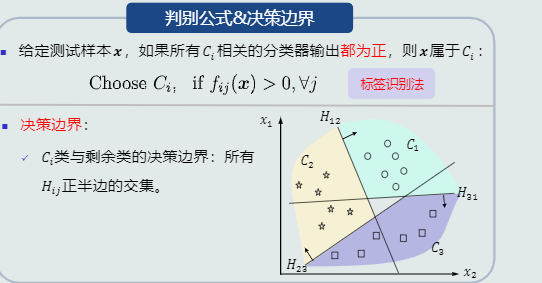
优势:适用于一些线性不可分的情况,从而实现非线性可分;无重叠区域
问题:出现拒绝选项
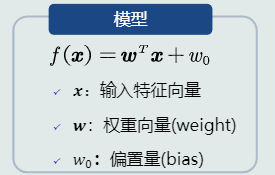
4.12 线性回归
- 模型表达


- 线性回归模型
- 学习参数W
- 目标函数

-
- 目标优化:梯度下降法、最小二乘法
4.13 逻辑回归的概念
- Logic变换


- Sigmoid函数

- Sigmoid函数:连接线性模型和后验概率的桥梁
- 线性模型f(x)+Sigmoid函数=后验概率
- 逻辑回归

-
- 决策边界

-
- 逻辑回归本身是一个非线性模型
- 用于分类:只能处理两个类别线性可分的情况
- 用于拟合:可拟合有限的非线性曲线
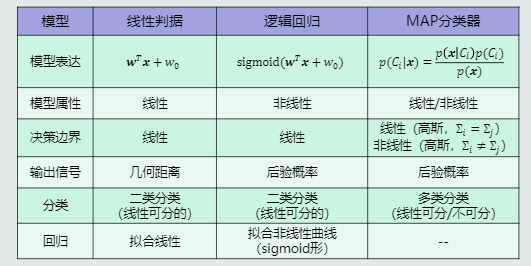
- 模型对比
4.14 逻辑回归的学习
- 学什么——学习参数w和w0
- 目标函数

- 目标函数优化——梯度下降法
- 梯度下降法注意问题:梯度消失问题(参数w尽量选择较小的初始值)
4.15 Softmax判据的概念

- Softmax判据——K个线性判据+softmax函数
- Softmax判据的决策过程

- Softmax判据的决策边界

- 适用范围
- 分类(前提是每个类与剩余类之间是线性可分)
- 回归(可以拟合指数函数exp形式的非线性曲线)
- Softmax判据本身是非线性模型
- 模型对比

4.16 Softmax判据的学习
- 学什么——学习k组参数
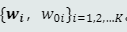
- 目标函数

- 目标函数优化:梯度下降法
4.17 核支持向量机
- 决策模型

- 核支持向量机:一个单隐层神经网络
- 对偶问题
- 常见核函数:多项式核函数、高斯核函数