>> A
A =
A =
1 2 10
3 4 12
5 6 15
3 4 12
5 6 15
B =
2 1 3
4 2 3
6 3 3
4 2 3
6 3 3
>> A .* B % Cij = Aij*Bij,行列数目都要一致
ans =
ans =
2 2 30
12 8 36
30 18 45
12 8 36
30 18 45
>> A*B%矩阵乘法
ans =
ans =
70 35 39
94 47 57
124 62 78
94 47 57
124 62 78
>>
>> A
A =
1 2 10
3 4 12
5 6 15
3 4 12
5 6 15
>> B =[1;2;3]
B =
B =
1
2
3
2
3
>> A .* B
ans =
ans =
1 2 10
6 8 24
15 18 45
6 8 24
15 18 45
>> A
A =
A =
1 2 10
3 4 12
5 6 15
3 4 12
5 6 15
>> #A
>> A .^2 %每个元素平方
>> A .^2 %每个元素平方
ans =
1 4 100
9 16 144
25 36 225
9 16 144
25 36 225
>> v =[1;2;3]
v =
v =
1
2
3
2
3
>> 1 ./v
ans =
ans =
1.00000
0.50000
0.33333
0.50000
0.33333
>> v v = 1 2 3 >> exp(v) ans = 2.7183 7.3891 20.0855 >> log(v) % loge(x) ans = 0.00000 0.69315 1.09861
>> abs([-1;2;-3])
ans =
ans =
1
2
3
2
3
>> v =[-1;-2;-4];
>> abs(v)
ans =
>> abs(v)
ans =
1
2
4
2
4
>> -v
ans =
ans =
1
2
4
2
4
v =
1
2
4
2
4
>> v + ones(length(v),1)
ans =
ans =
2
3
5
3
5
>> A A = 1 2 10 3 4 12 5 6 15 >> A+1 ans = 2 3 11 4 5 13 6 7 16 >> A A = 1 2 10 3 4 12 5 6 15 >> A ' %英文状态下的逗号 ans = 1 3 5 2 4 6 10 12 15
>> a = [1 15 2 0.5]
a =
a =
1.00000 15.00000 2.00000 0.50000
>> val =max(a)
val = 15
>> val = min(a)
val = 0.50000
val = 15
>> val = min(a)
val = 0.50000
>> [val ,ind] = max(a) % ind 为val的下标,按列来
val = 15
ind = 2
val = 15
ind = 2
>>A=[1 2;3 4;5 6] A = 1 2 3 4 5 6 >>[x ,y]=max(A,[],2)%行 x = 2 4 6 y = 2 2 2 >>[x ,y]=max(A,[],1)%列 x = 5 6 y = 3 3
>> a a = 1.00000 15.00000 2.00000 0.50000 >> a<3 %a中每一个元素与3比较,返回一个布尔值 ans = 1 0 1 1 >> find(a<3)%找到a中所有小于3的元素并返回它们的索引 ans = 1 3 4 >> A = magic(3) %生成幻方,常用这个函数便捷的生成一个3×3的矩阵 A = 8 1 6 3 5 7 4 9 2 幻方是整数'1:n^2'的排列,这样行和、列和和和对角线和都等于同一个值。 注意:N必须是大于或等于3的标量。
>>[r, c] = find(A >= 7) %找出A中大于等于7的元素,r,c分别表示它们的所在行、列
r =
1
3
2
c =
1
2
3
>> a a = 1.00000 15.00000 2.00000 0.50000 >> sum(a)
b
1
2
3
sum(b)=6
sum(a):a为一行/一列都可以计算总和 ans = 18.500 >> prod(a)%累乘积 ans = 15 >> a a = 1.00000 15.00000 2.00000 0.50000 >> floor(a)%向下取整 ans = 1 15 2 0 >> ceil(a)%向上取整 ans = 1 15 2 1 >> >> rand(3), rand(3)%生成2个矩阵 ans = 0.424057 0.954576 0.584581 0.122977 0.052602 0.109393 0.835577 0.895239 0.822539 ans = 0.586945 0.274731 0.046963 0.714344 0.297167 0.603440 0.141620 0.672273 0.901037 >> max(rand(3),rand(3))%# 取两个随机3X3矩阵中相同位置的较大值 组成的随机矩阵 ans = 0.73584 0.63209 0.27041 0.54327 0.25065 0.73805 0.91689 0.70591 0.82199
>> A A = 8 1 6
3 5 7 4 9 2 >> max(A,[],1)%每一列的最大值 ans = 8 9 7 >> max(A,[],2)%每一行的最大值 ans = 8 7 9 >> >> max(A)%m第I行和第I列的所有元素中的最大值 ans = 8 9 7
# 求矩阵最大元素 ٴ>> max(max(A)) %等价于max(A(:)) ans = 9 >> B B = 1 2 3 >> sum(B,1)%列 ans = 6 >> sum(B,2)%行 ans = 1 2 3
A =
47 58 69 80 1 12 23 34 45
57 68 79 9 11 22 33 44 46
67 78 8 10 21 32 43 54 56
77 7 18 20 31 42 53 55 66
6 17 19 30 41 52 63 65 76
16 27 29 40 51 62 64 75 5
26 28 39 50 61 72 74 4 15
36 38 49 60 71 73 3 14 25
37 48 59 70 81 2 13 24 35
57 68 79 9 11 22 33 44 46
67 78 8 10 21 32 43 54 56
77 7 18 20 31 42 53 55 66
6 17 19 30 41 52 63 65 76
16 27 29 40 51 62 64 75 5
26 28 39 50 61 72 74 4 15
36 38 49 60 71 73 3 14 25
37 48 59 70 81 2 13 24 35
>> sum(A,1) ans = 369 369 369 369 369 369 369 369 369
>> A.*eye(9)
ans =
ans =
47 0 0 0 0 0 0 0 0
0 68 0 0 0 0 0 0 0
0 0 8 0 0 0 0 0 0
0 0 0 20 0 0 0 0 0
0 0 0 0 41 0 0 0 0
0 0 0 0 0 62 0 0 0
0 0 0 0 0 0 74 0 0
0 0 0 0 0 0 0 14 0
0 0 0 0 0 0 0 0 35
0 68 0 0 0 0 0 0 0
0 0 8 0 0 0 0 0 0
0 0 0 20 0 0 0 0 0
0 0 0 0 41 0 0 0 0
0 0 0 0 0 62 0 0 0
0 0 0 0 0 0 74 0 0
0 0 0 0 0 0 0 14 0
0 0 0 0 0 0 0 0 35
>> sum(A.*eye(9))%列
ans =
ans =
47 68 8 20 41 62 74 14 35
>> sum(sum(A.*eye(9)))%只有一行,累加和
ans = 369
>> eye(9) ans = Diagonal Matrix 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 >> flipud(eye(9)) ans = Permutation Matrix 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 >> A.*flipud(eye(9))%A的副对角线 ans = 0 0 0 0 0 0 0 0 45 0 0 0 0 0 0 0 44 0 0 0 0 0 0 0 43 0 0 0 0 0 0 0 42 0 0 0 0 0 0 0 41 0 0 0 0 0 0 0 40 0 0 0 0 0 0 0 39 0 0 0 0 0 0 0 38 0 0 0 0 0 0 0 37 0 0 0 0 0 0 0 0 >> sum(A.*flipud(eye(9))) ans = 37 38 39 40 41 42 43 44 45 >> sum(sum(A.*flipud(eye(9))))%flipud表示使矩阵垂直翻转,可以用来求矩阵A的副对角线之和 ans = 369
>> A =magic(3) A = 8 1 6 3 5 7 4 9 2 >> A' ans = 8 3 4 1 5 9 6 7 2 >> pinv(A)%逆矩阵 ans = 0.147222 -0.144444 0.063889 -0.061111 0.022222 0.105556 -0.019444 0.188889 -0.102778 >> A*pinv(A) ans = 1.0000e+00 -1.2157e-14 6.3560e-15 5.5511e-17 1.0000e+00 -1.5266e-16 -5.9813e-15 1.2268e-14 1.0000e+00
>> t =[0:0.01:0.98]; >> y1 =sin(8*pi*t); >> plot(t,y1)

T = 2*pi/8*pi =0.25
>> y2 =cos(8*pi*t); >> plot(t,y2)
>> plot(t,y1); >> hold on; >> plot(t,y2,'r');%y2绘制在y1上,y2用红色描绘
>> legend('sin','cos') >> title('my plot')

%先切换目录 >> cd 'E:dasandedasiokafterdeep learningmaterial' >> pwd ans = E:dasandedasiokafterdeep learningmaterial %保存到该目录下 >> print -dpng 'myplot.png'
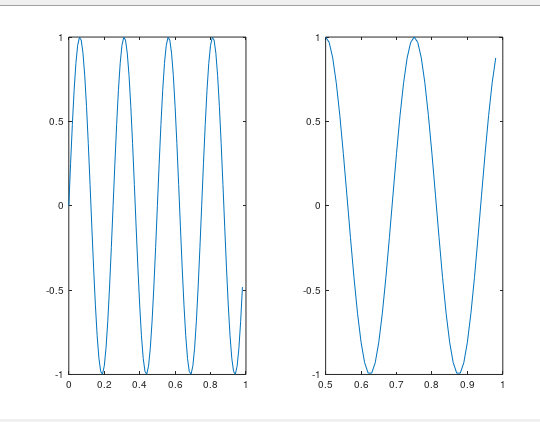
>> close%关闭图片窗口 >> figure(2);plot(t,y1);%为图片标号 >> subplot(1,2,1);%分为1*2的格子,现在用第一个 >> plot(t,y1); >> subplot(1,2,2); >> plot(t,y2); >> axis([0.5 1 -1 1])%改变右图的坐标轴
>> clf%清除
>> A =magic(5) A = 17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9 >> imagesc(A)%可视化矩阵A,不同的颜色代表不同的数值】 >> imagesc(A),colorbar,colormap gray;可视化矩阵A,颜色条,颜色位图 。 用逗号连接函数调用或者命令
>> a =1,b =2
a = 1
b = 2
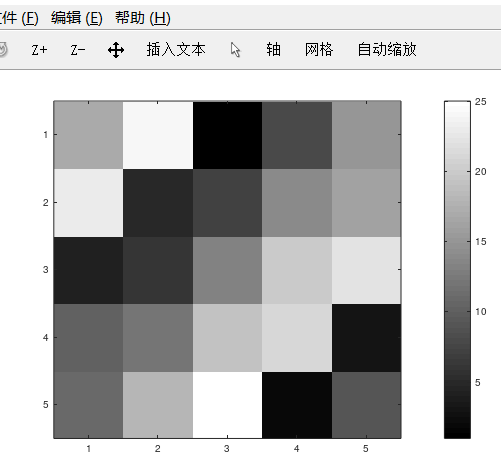
如: 上图的【5 4】为2 对应颜色条较黑色