Speaker:Andrew Ng
这一次主要讲解的是单变量的线性回归问题。
1.Model Representation
先来一个现实生活中的例子,这里的例子是房子尺寸和房价的模型关系表达。
通过学习Linear Regression可以进行预测某一size的房子prices是多少。

Regression问题属于Supervised Learning监督学习问题,预测连续值,Classification分类是预测离散值,上一个Introduction已经介绍过。

在上一张图的坐标点就是这里的训练集合。这里我们定义m是训练数据的数量或组数,x是输入变量或特征feature,y是输出变量target。) 代表一组训练数据,例如
代表一组训练数据,例如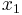 = 2104,
= 2104, 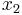 = 1416,
= 1416, 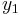 = 460.
= 460.

图的左半边表达的就是进行Price预测的流程,关键就在与如何得到h(Hypothesis),它表示了x(Size of house)和y(Price)之间的一种关系。得到这个关系h我们就可以来根据给定的x来预测y的值。 那么h如何来表达呢?因为是单变量的线性回归,那么可以设
= heta_0+ heta_1x) 也可以简写成
也可以简写成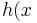) .那么我们如何来计算他的参数
.那么我们如何来计算他的参数 和
和 ?下面继续。
?下面继续。2.Cost Function
这里讲述如何定义损失函数Cost Function来得到 和
和 的值。
的值。
 和
和 的值。
的值。思路 Idea : Choose  ,
, so that
so that ) is close to
is close to 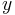 for out training examples
for out training examples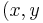) .
.
 ,
, so that
so that ) is close to
is close to 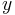 for out training examples
for out training examples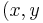) .
.这里我们定义最小平方误差公式:

这张图是关键,一定要明确我们的问题是什么。目标就是能使Goal最小化的 的参数值就是我们要求的。
的参数值就是我们要求的。

这里Andrew Ng举例了一个在最小平方误差公式下, 的情况,那么
的情况,那么) 就是一个二次函数,取到极值点就就是最小对应的参数值就是我们需要的答案。这个比较简单,这里不再赘述了。
就是一个二次函数,取到极值点就就是最小对应的参数值就是我们需要的答案。这个比较简单,这里不再赘述了。

回归到原来的问题,我们应该如何去找这样的参数值使得J最小呢。

思路就是,初始化 ,不断的改变他们的值,使得Cost Function
,不断的改变他们的值,使得Cost Function) 不断减小,知道在一个最小值的位置为止。
不断减小,知道在一个最小值的位置为止。
这里我们使用梯度下降的方法来寻找这个值,向下面的图一样,初始时候站在山顶,然后从山顶一路快速冲下山。


不同的初始化参数的位置可能导致取到不同的最小值,所以梯度下降算法得到是局部最优值。
梯度下降算法,Gradient Descent Algorithm如下:
repeat until convergence {
}

这个图反应的是Learning Rate对于梯度下降算法的影响。

梯度下降方法收敛到一个局部最小值,即使用一个固定的Learning Rate。当我们将要得到局部最小值时候,梯度也在不断变缓,放慢 变化速率,自动的小幅度像局部最优点靠近。
变化速率,自动的小幅度像局部最优点靠近。
最后计算偏导数我们得到的公式如下:


这种叫做Batch Gradient Descent 批量梯度下降法,使用所有的训练样本来计算) .
.
3.Question
Let  ne some function so that
ne some function so that ) outputs a number. For this problem,
outputs a number. For this problem, is some arbitrary/unknown smooth function(not necessarily the cost function of linear regression, so
is some arbitrary/unknown smooth function(not necessarily the cost function of linear regression, so  is may have local optima).Suppose we use gradient descent to try to minimize
is may have local optima).Suppose we use gradient descent to try to minimize ) as ia function of
as ia function of  and
and  . Which of the following statements are true.
. Which of the following statements are true.
1. 如果Learning Rate过大,可能会出现overshoot the minimum现象,超过了最小点并且有可能收敛失败,产生diverge。
2. 初始化对于最后找到的结果是有影响的,梯度下降的最后结果有可能找到不同的局部最优。
初始化对于最后找到的结果是有影响的,梯度下降的最后结果有可能找到不同的局部最优。
3.如果 初始化刚好在了全局最优的位置,那么梯度为0,
初始化刚好在了全局最优的位置,那么梯度为0, 不会在改变了。
不会在改变了。
4.如果Learning Rate过小,那么梯度下降每次只能走一小步,需要很长时间去收敛Converge。
Suppose that for some linear regression problem (say, predicting housing prices as in the lecture), we have some training set, and for our training set we managed to find some  such that
such that =0) ,Which of the statements below must then be true?
,Which of the statements below must then be true?
1. 如果所有的Training Examples 能够在一条直线上=0) 是可能的。
是可能的。
2.=0) 的情况下对于所有的Examples
的情况下对于所有的Examples},{y}^{(i)})) 中,
中,})={y}^{(i)}) 。
。
3.对于这题的) 线性回归问题, 除去全局最优它不存在局部最优,所以不可能卡在某一个局部最优位置。
线性回归问题, 除去全局最优它不存在局部最优,所以不可能卡在某一个局部最优位置。