A. Energy Conversion
 View Code
View Code
 View Code
View Code
 View Code
View Code
+v[i][j]&space;&&&space;k<i&space;\&space;dp[k][j-1]+v[i][j]&space;&&&space;k=i&space;\&space;dp[k][j-1]+sum(i+1,k)+v[i][j]&space;&&&space;k>i&space;end{matrix}
ight.)
 View Code
View Code
小度有M点能量,打开石门需要N点能量,他可以有一个操作使用V点能量让自己当前能量变成(M-V)*K,问最少需要几次能量转换才能打开石门,打不开输出-1.
N,M,V,K <= 10 ^ 8
a.模拟能量转换过程,如果发现能量转换后保持不变,或者能量变小,答案就是-1,否则输出模拟后的答案。因为K肯定会大于2,所以收敛到N还是很快的。

#define _CRT_SECURE_NO_WARNINGS #include <cstdio> #include <iostream> #include <cstring> #include <algorithm> #include <cmath> #include <map> #include <vector> #include <queue> #include <cstdlib> #include <set> #include <numeric> using namespace std; int main() { int t; scanf("%d", &t); __int64 n, m, v, k, ans; while (t--) { scanf("%I64d %I64d %I64d %I64d", &n, &m, &v, &k); if (m >= n) ans = 0; else if ((m - v)*k >= n) ans = 1; else if (k==1) ans = -1; else { __int64 kk = k; __int64 cur = 0; for (int i = 1;; i++) { long long val = m * kk + v * k * (kk - 1) / (1 - k); if (val <= cur) { ans = -1; break; } if (val >= n) { ans = i; break; } cur = val; kk *= k; } } printf("%I64d ", ans); } }
b.进行数值分析,当K不等于1是,n次后能得到的能量为=MK^{n}-Vfrac{K(1-K^{n})}^{1-K}) ,我们保证它的导数是大于0,那么当f(n)=M时候,求得n就是答案。
,我们保证它的导数是大于0,那么当f(n)=M时候,求得n就是答案。

#define _CRT_SECURE_NO_WARNINGS #include <cstdio> #include <iostream> #include <cstring> #include <algorithm> #include <cmath> #include <map> #include <vector> #include <queue> #include <cstdlib> #include <set> #include <numeric> using namespace std; int main() { int t; scanf("%d", &t); double n, m, v, k; int ans; while (t--) { scanf("%lf %lf %lf %lf", &n, &m, &v, &k); if (m >= n) ans = 0; else if ((m - v)*k >= n) ans = 1; else { if (k == 1) { ans = -1; } else { if (m + v * k /(1 - k) <= 0) ans = -1; else { ans = ceil(log(((1 - k)*n + v*k) / ((1 - k)*m + v*k)) / log(k)); if (ans < 2) ans = -1; } } } printf("%d ", ans); } }
B. Disk Schedule
双调路径,DP动态规划
C. Xor Num
描述:
Problem Description
Zeus 和 Prometheus 做了一个游戏,Prometheus 给 Zeus 一个集合,集合中包含了N个正整数,随后 Prometheus 将向 Zeus 发起M次询问,每次询问中包含一个正整数 S ,之后 Zeus 需要在集合当中找出一个正整数 K ,使得 K 与 S 的异或结果最大。Prometheus 为了让 Zeus 看到人类的伟大,随即同意 Zeus 可以向人类求助。你能证明人类的智慧么?
Input
输入包含若干组测试数据,每组测试数据包含若干行。
输入的第一行是一个整数T(T < 10),表示共有T组数据。
每组数据的第一行输入两个正整数N,M(<1=N,M<=100000),接下来一行,包含N个正整数,代表 Zeus 的获得的集合,之后M行,每行一个正整数S,代表 Prometheus 询问的正整数。所有正整数均不超过2^32。
输入的第一行是一个整数T(T < 10),表示共有T组数据。
每组数据的第一行输入两个正整数N,M(<1=N,M<=100000),接下来一行,包含N个正整数,代表 Zeus 的获得的集合,之后M行,每行一个正整数S,代表 Prometheus 询问的正整数。所有正整数均不超过2^32。
思路:对于一个正整数S如何找一个数X,让S ^ X最大,最简单的方法就是,X的每一位与S的每一位是相反的。那么对于S集合中的所有数就可以构造一棵Trie树进行记录,寻找时候就S当前位取反的方向向下查找(如果存在,否则向另一个方向),直到遍历完S的每一位,也就从Trie树得到答案。构造Trie树的复杂度为O(32*N),每次查询的复杂度为O(32),Trie空间复杂度理论为(2^32),但是最多只有N个整数,所以是不会太大。

#define _CRT_SECURE_NO_WARNINGS #include <cstdio> #include <iostream> #include <cstring> #include <algorithm> #include <cmath> #include <map> #include <vector> #include <queue> #include <cstdlib> #include <set> #include <numeric> #include <bitset> using namespace std; const int branchNum = 2;//字数的个数 class TrieNode { public: TrieNode *next[branchNum]; TrieNode() { memset(next, NULL, sizeof(next)); } }; class Trie { public: Trie(); void Insert(int val); unsigned long Find(int val); void DeleteTrie(TrieNode *root); TrieNode *Root; }; Trie::Trie() { Root = new TrieNode(); } void Trie::Insert(int val) { TrieNode *location = Root; for (int i = 31; i >= 0; i--) { int v = val >> i; if (location->next[v & 0x01] == NULL)//不存在就建立节点 { TrieNode *tmp = new TrieNode(); location->next[v & 0x01] = tmp; } location = location->next[v & 0x01]; } } unsigned long Trie::Find(int val) { bitset<32> res; TrieNode *location = Root; for (int i = 31; i >= 0; i--) { int v = val >> i; if (v & 0x01) { if (location->next[0] != NULL) { location = location->next[0]; res[i] = 0; } else { location = location->next[1]; res[i] = 1; } } else { if (location->next[1] != NULL) { location = location->next[1]; res[i] = 1; } else { location = location->next[0]; res[i] = 0; } } } return res.to_ulong(); } void Trie::DeleteTrie(TrieNode *root) { for (int i = 0; i < branchNum; ++i) { if (root->next[i] != NULL) { DeleteTrie(root->next[i]); } } delete root; } int main() { int t, n, m, i, e; scanf("%d", &t); for (int Cas = 1; Cas <= t; Cas++) { scanf("%d %d", &n, &m); Trie t; for (i = 0; i < n; i++) { scanf("%d", &e); t.Insert(e); } printf("Case #%d: ", Cas); while (m--) { scanf("%d", &e); printf("%u ", t.Find(e)); } } return 0; }
D. Labyrinth
题意就是给定一个矩阵,每个单元元素可以使正、负、0,起始点在左上角,终止点在右上角,每次只能上、下、右三种移动方式,并且一个格子只能走一次,问得到的最大值。
用动态规划来求解,定义dp[i][j],代表从(1, 1)走到第(i, j)个格子时候得到的最大值,那么最后的答案就是dp[1][m]。
现在只考虑两列:
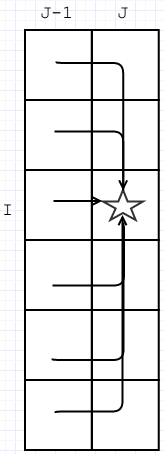
我们要求dp[i][j]的值,它可以来自于J-1列的各个单元,那么可以得到递推的方程如下:
其中k是枚举第j-1列的各行单元,v代表矩阵中存储的值,sum(k, i-1),代表求第j列的第k行到i-1行的和。由于每一列只和前面的一列相关,还可以用滚动数组来进行空间优化的。
那么最后得到dp[1][m]就是需要的值。

#define _CRT_SECURE_NO_WARNINGS #include <cstdio> #include <iostream> #include <cstring> #include <algorithm> #include <cmath> #include <map> #include <vector> #include <queue> #include <cstdlib> #include <set> #include <numeric> #include <bitset> using namespace std; const int maxn = 105; int e[maxn][maxn]; int dp[maxn][maxn]; int sum[maxn][maxn]; int main() { int t, i, j, k, r, c; scanf("%d", &t); for (int Cas = 1; Cas <= t; Cas++) { scanf("%d %d", &r, &c); for (i = 1; i <= r; i++) for (j = 1; j <= c; j++) scanf("%d", &e[i][j]); memset(sum, 0, sizeof(sum)); for (i = 1; i <= c; i++) for (j = 1; j <= r; j++) { sum[j][i] = sum[j - 1][i] + e[j][i]; } memset(dp, 0, sizeof(dp)); dp[1][1] = e[1][1]; for (i = 1; i <= r; i++) { dp[i][1] = dp[i - 1][1]+e[i][1]; } for (i = 2; i <= c; i++) for (j = 1; j <= r; j++) { dp[j][i] = -0x3fffffff; for (k = 1; k <= r; k++) { int tmp; if (k == j) { tmp = e[j][i]; } else if (k > j) { tmp = sum[k][i] - sum[j][i] + e[j][i]; } else { tmp = sum[j - 1][i] - sum[k - 1][i] + e[j][i]; } dp[j][i] = max(dp[j][i], dp[k][i - 1] + tmp); } } printf("Case #%d: ", Cas); printf("%d ", dp[1][c]); } return 0; }
