N皇后问题(位运算实现)

本文参考Matrix67的位运算相关的博文。

顺道列出Matrix67的位运算及其使用技巧 (一) (二) (三) (四)，很不错的文章，非常值得一看。

    主要就其中的N皇后问题，给出C++位运算实现版本以及注释分析。

    皇后问题很经典，就不再赘述问题本身，解决皇后问题，一般采用的都是深搜DFS+回溯的方法，按照行(列)的顺序枚举每一个可以放置的情况，然后进行冲突判断，当前的放置是否合法，合法就继续搜索下一层，不合法就搜索就回溯。直到，找到一个合法的解，每一层都有一个皇后并且不发生冲突，这时候，放置的方案数计1.

    位运算也是采用的也是深搜加回溯的方法，但是优点在于使用位运算进行冲突的检测，这使代码简洁高效，而且还加快了运行速度。

    下面的两张图来自Matrix67的(三):

                                            

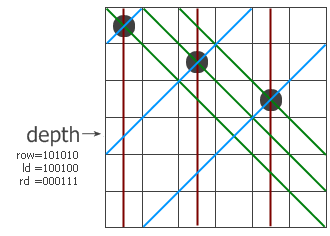
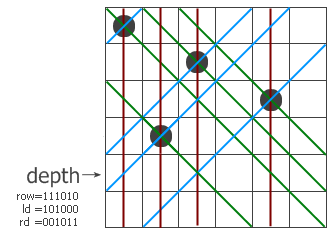
    depth 表示当前要进行搜索的层，row的二进制表示当前层二进制为1是冲突列，ld表示从右上角到左下角对角线冲突关系，rd表示的从左上角到右下角的冲突关系。

    具体实现代码如下：

#include <iostream>
#include <cstdio>
#include <ctime>
using namespace std;

const int N = 16; // 求解N皇后， N不能超过int的bits
int upper_limit = (1 << N) - 1; // 111...1111 n bits
int ans = 0;

void test(int row, int ld, int rd) {
    // 如果row的皇后还没有放满
    if (row != upper_limit) {
        // (row|ld|rd)表示行row，右上到左下ld，左上到右下rd对角线，为1则是不能放的位置， 取~后表示能放置的位置
        // 因为是用的int 32位存的，所以N位向上的高位需要重新置成0
        // 所以再和upper_limit取&操作，就提取出所有可以放置皇后的位置
        int pos = upper_limit & ~(row | ld | rd);
        
        // while 循环枚举所有为1的位置，然后去放置皇后
        while (pos != 0) {
            // 和树状数组的lowbit一样，提取出pos的二进制最后一个1所在的位置的值
            // 也可以写成x & (x^(x-1))
            int p = pos & (-pos);  
            
            pos = pos ^ p; // 将p二进制为1的位置在pos中置为0
            // row | p 把p二进制为1的位置放上皇后
            // (ld | p) << 1 更新ld的下一层不能放的位置
            // (rd | p) >> 1 更新rd的下一层不能放的位置
            test(row|p, (ld|p) << 1, (rd|p) >> 1);
        }
    } else ans++;

}

int main() {
    ans = 0;
    clock_t start, finish;
    double duration;
    start = clock();
    test(0, 0, 0);
    finish = clock();
    duration = (double)(finish-start) / CLOCKS_PER_SEC;
    printf("Time is %lf
", duration); 
    printf("共有多少种情况: %d
", ans);
    return 0;
}

分析：

位运算版本确实在代码编写和时间效率上都相当棒

代码的关键部分，就在于处理row，ld，rd搜索时候的禁位变化

当处理超过int可表示位数时候，这时候就要抛弃整型，使用bitset或者位结构去做相关操作