图论笔记第四章 欧拉图与哈密尔顿图(beta.)
主要内容
注:ppt-2-word 有公式 乱套。
摘要:考点, 找欧拉环游,还有辨认 欧拉图,还有H图
定理2 若W是包含图G的每条边至少一次的闭途径,则W具有最小权值当且仅当下列两个条件被满足:
(1) G的每条边在W中最多重复一次;
(2) 对于G的每个圈上的边来说,在W中重复的边的总权值不超过该圈非重复边总权值。
一、欧拉图与中国邮路问题
二、哈密尔顿图
三、度极大非哈密尔顿图与TSP问题
教学时数
安排8学时讲授本章内容
四、超哈密尔顿图问题
本次课主要内容
(一)、欧拉图及其性质
(二)、Fleury算法
(三)、中国邮路问题
欧拉图与中国邮路问题
1、欧拉图的概念
(2)、欧拉图概念
定义1 对于连通图G,如果G中存在经过每条边的闭迹,则称G为欧拉图,简称G为E图。欧拉闭迹又称为欧拉环游,或欧拉回路。
2、欧拉图的性质
定理1 下列陈述对于非平凡连通图G是等价的:
(1) G是欧拉图;
(2) G的顶点度数为偶数;
(3) G的边集合能划分为圈。
证明: (1)→(2)
由(1),设 C是欧拉图G的任一欧拉环游,v是G中任意顶点,v在环游中每出现一次,意味在G中有两条不同边与v关联,所以,在G中与v关联的边数为偶数,即v的度数为偶数,由v的任意性,即证明(2)。
(2)→(3)
由于G是连通非平凡的且每个顶点度数为偶数,所以G中至少存在圈C1,从G中去掉C1中的边,得到G的生成
子图G1,若G1没有边,则(3)成立。否则,G1的每个非平凡分支是度数为偶数的连通图,于是又可以抽取一个圈。反复这样抽取,E(G)最终划分为若干圈。
(3)→(1)
设C1是G的边划分中的一个圈。若G仅由此圈组成,则G显然是欧拉图。
否则,由于G连通,所以,必然存在圈C2,它和C1有公共顶点。于是,C1∪C2是一条含有C1与C2的边的欧拉闭迹,如此拼接下去,得到包含G的所有边的一条欧拉闭迹。即证G是欧拉图。
推论1 连通图G是欧拉图当且仅当G的顶点度数为偶。
推论2 连通非欧拉图G存在欧拉迹当且仅当G中只有两个顶点度数为奇数。
例1 下面图中谁是欧拉图?谁是非欧拉图但存在欧拉迹?谁是非欧拉图且不存在欧拉迹?
解:G1是欧拉图;G2是非欧拉图,但存在欧拉迹;G3中不存在欧拉迹。
(二)、Fleury算法
该算法解决了在欧拉图中求出一条具体欧拉环游的方法。方法是尽可能避割边行走。
1、 算法
(1)、 任意选择一个顶点v0,置w0=v0;
(2)、 假设迹wi=v0e1v1…eivi已经选定,那么按下述方法从E-{e1,e2,…,ei}中选取边ei+1:
1)、 ei+1与vi相关联;
2)、除非没有别的边可选择,否则 ei+1不能是
Gi=G-{e1,e2,…,ei}的割边。
(3)、 当(2)不能执行时,算法停止。
例3 在下面欧拉图G中求一条欧拉回路。
解:
例4 某博物馆的一层布置如下图,其中边代表走廊,结点e是入口,结点g是礼品店,通过g我们可以离开博物馆。请找出从博物馆e进入,经过每个走廊恰好一次,最后从g处离开的路线。
解:图中只有两个奇度顶点e和g,因此存在起点为e,终点为g的欧拉迹。
为了在G中求出一条起点为e,终点为g的欧拉迹,在e和g间添加一条平行边m
…
用Fleury算法求出欧拉环游为:
emgcfabchbdhgdjiejge
所以:解为:egjeijdghdbhcbafcg
证明:令Wn=v0e1v1…envn为由Fleury算法得到的一条G中迹。
定理1 若G是欧拉图,则G中任意用Fleury算法作出的迹都是G的欧拉环游。
3、算法复杂性分析
设G=(n, m)是欧拉图
由Fleury算法知:算法需要m次循环;
算法中主要运算是判断: ,该判断的时间复杂性是n2数量级的。
所以Fleury算法时间复杂性是:O(n
(三)、中国邮路问题
1962年,中国数学家管梅谷提出并解决了“中国邮路问题”
1、问题
邮递员派信的街道是边赋权连通图。从邮局出发,每条街道至少行走一次,再回邮局。如何行走,使其行走的环游路程最短?
如果邮路图本身是欧拉图,那么由Fleury算法,可得到他的行走路线。
如果邮路图本身是非欧拉图,如何重复行走街道才能使行走总路程最短?
2、管梅谷的结论
定理2 若W是包含图G的每条边至少一次的闭途径,则W具有最小权值当且仅当下列两个条件被满足:
(1) G的每条边在W中最多重复一次;
(2) 对于G的每个圈上的边来说,在W中重复的边的总权值不超过该圈非重复边总权值。
证明:“必要性”
首先,设G是连通非欧拉图,u与v是G的两个奇度顶点,把连接u与v的路上的边改为2重边,则路中的点的度数奇偶性没有改变,仍然为偶数,但u与v的度数由奇数变成了偶数。如果对G中每对奇度点都如此处理,则最终得到的图为欧拉图。设该图为G1.
其次,对G1作修改:
如果在G1中,边e重复数大于2,则在G1中删掉2条重复的e边后,所得之图仍然是包含G的欧拉图。
在G1中,对每组平行边都做上面的处理,最后得到一个重复边数最多为1的包含G的欧拉图G2。
这说明,若W是包含G的所有边的欧拉环游,则G中每条边至多在W里出现两次。这就证明了(1).
又设C是G2中任意一个圈,在该圈中,如果重复边的总权值超过该圈中非重复边总权值,那么可以把该圈中平行边改为非平行边,而把非平行边改为平行边,如此修改,得到的图仍然是包含G的欧拉图,但对应的欧拉环游长度减小了。
所以:
注: 定
理2的证明过程实际上给出了求中国邮路问题的方法.下面看一个例题。
所以: 这就是说,只要对G2的每个圈都作上面的修改,最后得到的 解:由定理2:图仍
然为包含
G的欧拉
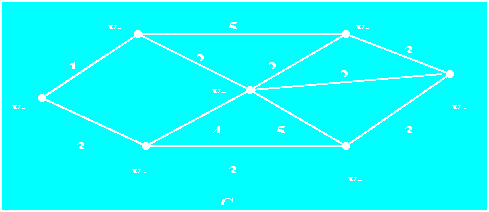
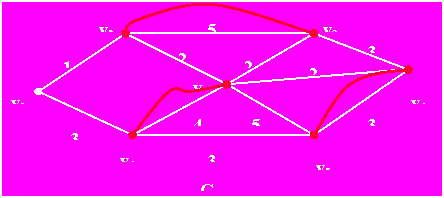
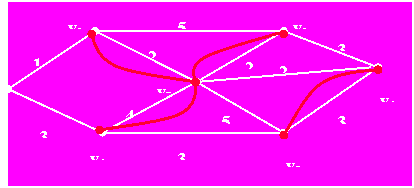
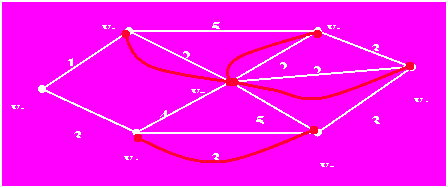
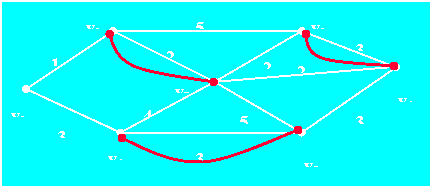
例5 求包含下图G的一个最优欧拉环游。
v1
所以:图,而最后的图正好满足(2).
例6 如果一个非负权的边赋权图G中只有两个奇度顶点u与v,设计一个求其最优欧拉环游的算法。
解: 1、 算法
(1)、 在u与v间求出一条最短路P; (最短路算法)
(2)、 在最短路P上,给每条边添加一条平行边得G的欧拉母图G*;
“充分 由断言2很容易得到:性”
(3)、 在G的欧拉母图G* 中用Fleury算法求出一条欧拉环游。
2、 算法证明
只需证明:任
何两条包含G中 定理:用上面方法求出的欧拉环游是最优欧拉环游。
又因为:所有边的闭途径W1与W2,如果满足定理2的两个条件,则
它们有相同的总权值。 证明:设u与v是G的两个奇度顶点,G*是G的任意一个欧拉母图。
考虑G*[E*-E], 显然它只有两个奇数顶点u与v, 当然它们必须在G*[E*-E]的同一个分支中,因此,存在(u, v)路P*.
设Y1与Y2分别表示W
1与W2中重复出现的边集合。 所以,
我们先证明:对于任意一个圈C*,如果满
足:
即证明定理。 有:
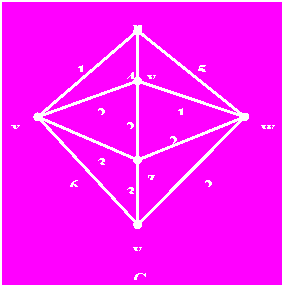
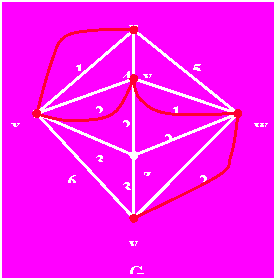
例如:求出下图的一条最优欧拉环游。
1:G[Y]的
每个顶点度数必然为偶数。
最优欧拉环游:x u y w v z w y x u w v x z y x
令:Y= (Y1-Y2)∪ (Y2-Y1)
作业