1. 感知器的介绍
感知器学习算法(PLA:Perception Learning Algorithm)是1957年提出的算法,比svm要早,实际上他是一种二分类问题的超平面(超平面是比实际维数低一维的集合,可以理解为这个集合的正交补空间的维数为1),一旦我们找到了这个超平面,我们就可以用来执行二分类问题。给出增强向量  和
和 ,感知器就可以使用假设函数去分类数据点
,感知器就可以使用假设函数去分类数据点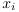 :
:

其中,

2. 感知器的算法
从上式中我们可以发现,我们需要的就是找到一个 ,找到了一个
,找到了一个 ,就是找到了一个超平面,那么我们可以理解为,
,就是找到了一个超平面,那么我们可以理解为,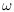 是唯一的参数。因此,我们只需要找到这样的超平面就可以了。算法描述如下所示[2]:
是唯一的参数。因此,我们只需要找到这样的超平面就可以了。算法描述如下所示[2]:
1.随机定义一个超平面,用来分类数据
2.找出其中错误的一个例子,通过改变 来重新更新超平面
来重新更新超平面
3.用新的超平面来分类数据
4.重复步骤2 3 直到没有错误的例子出现
import numpy as np def perceptron_learning_algorithm(X, y): w = np.random.rand(3) #随机生成一个超平面 misclassified_examples = predict(hypothesis, X, y, w)#找出其中判别错误的例子 while misclassified_examples.any():#直到错误的例子为0,停止 x, expected_y = pick_one_from(misclassified_examples, X, y)#从错误的例子中随机选取一个例子 w = w + x * expected_y #更新超平面 misclassified_examples = predict(hypothesis, X, y, w)#重新找出错误的例子 return w
3. 感知器的更新规则
在更新超平面中,,我们随机选择一个错误分类,让感知器去感知他,我们可以使用 与
与 的点积去判断其分类是否错误。因为在
的点积去判断其分类是否错误。因为在 中,若果预测结果为1,那么二者夹角小于90度,我们就要增大它,如果预测结果为-1,那么二者夹角大于90度,我们就要缩小它。通过这样的操作,我们最终可以让所有的x与w垂直。如下图所示:
中,若果预测结果为1,那么二者夹角小于90度,我们就要增大它,如果预测结果为-1,那么二者夹角大于90度,我们就要缩小它。通过这样的操作,我们最终可以让所有的x与w垂直。如下图所示:

如果两个向量的夹角小于90度,那么我们就要加大它,两个向量大于90度,那么我们就要减小它。即使用 ,
,  来增加角度与减小角度。如下两图所示:
来增加角度与减小角度。如下两图所示:

相加运算产生了一个小的夹角

相减运算产生了一个大的夹角
我们便可以通过这个算法,不断调整w,使得我们找到我们的w
def update_rule(expected_y, w, x): if expected_y == 1: w = w + x else: w = w - x return w
还要注意到有时我们碰到特殊的x,当⽤修改规则调整w时会使以前正确的分类变成错误的。所以,假设函数会在调整之后变得更糟!⼀个解决办法仅在发现修改w之后让错误分类的例⼦减少时才使⽤。这样修改之后的PLA就是⼴为⼈知的⼝袋算法 。
同时,改变超平面参数的也可以使用梯度下降法等方法,在这里就不再赘述,以后会详细讲到。
4. 感知器的收敛性
这里有一个很严重的问题,我们一直在强调我们修改规则能够让错误点消失,但是我们能确定这个目的而不会出现某个数据集出现发散的情况吗?数学家已经注意到这个问题了,感知器收敛理论,由Novikoff 在1963年提出,由兴趣的小伙伴们可以去搜索看一下。
5. 感知器的局限性
我们知道,PLA使用的是随机权重与随机错误用例,这样带来的后果就是低效率,同时即使我们最后找到了一个平面,这个平面的确可以让两类分离,但是我们想要的是方差最小,即点到平面的距离能够最小,才能称作一个非常好的分类器。一个好的分类器应该具有很好的泛化性能,因此如何让我们的分类器能够具有很好的泛化性能,这边是SVM需要做的事情。
6. 参考文献
[1] Toby Segaram <<集体智慧编程>>
[2] Alexander Kowalczyk <<Support Vector Machines Succinctly>>
[3] 张重生 << 大数据分析>>