单调栈 专题训练

简介

一、定义

单调栈是一种高效，方便，简单的数据结构，其特点与单调队列类似，满足在栈里的数据呈现单调递增或者递减的特性，用来计算一定区间的值。

二、原理

(1)当新元素在单调性上优于栈顶时（单增栈新元素比栈顶大，单减栈新元素比栈顶小），压栈，栈深+1；

(2)当新元素在单调性与栈顶相同（新元素于栈顶相同）或劣于栈顶时（单增栈新元素比栈顶小，单减栈新元素比栈顶大），弹栈，栈深-1；

(3)根据题目条件计算栈变动后的最优值。

三、实现形式

STL的stack库，数组+栈顶指针

四、几点注意

1. 数据类型$long long$，建议$scanf$不要漏掉$lld$。
2. 注意栈空的情况，此时无法取栈顶元素或者弹栈。
3. 注意旧元素的延展性和新元素的继承性。

例题

洛谷 P3467 海报PLA

基本思路

当新元素与栈内某元素相同时，海报可以共用，因此海报数-1,。于是我们只需计算，若高度不同的时候，海报数+1，若相同，则海报数不变，其他遵守单调栈规则。

#include<bits/stdc++.h>
#define FOR(i,a,b) for(int i=a;i<b;i++)
#define FOR2(i,a,b) for(int i=a;i<=b;i++)
#define ll long long
#define INF  0x7f7f7f7f;
#define MAXN 2600100
#define MOD 10007
using namespace std;
ll arr[MAXN];
ll n,ans=0;
stack<ll>s;
int main()
{
    cin>>n;
    FOR(i,0,n)
    {
        ll w;cin>>w>>arr[i];
        while(!s.empty()&&s.top()>=arr[i])
        {
            if(s.top()!=arr[i])
            {
                ans++;
            }
            s.pop();
        }
        s.push(arr[i]);
    }
    cout<<ans+s.size()<<endl;
    return 0;
}

 洛谷 SP1805 HISTOGRA - Largest Rectangle in a Histogram

基本思路

每一列记录三个元素，当前高度$h$，左边扩展的最远的列数$l$，右边扩展最远的列数$r$。

当一个新元素要入栈时，若新元素$h$>栈顶$h$，则栈内元素的右边界扩展到等于新元素所在列（站内元素$h$均小于新元素$h$）；

若新元素$h$<=栈顶$h$，则栈顶元素出栈，记录此时最大值，和栈顶元素的右边界$rr$；出栈后新的栈顶元素的右边界扩展到$rr$，计算此时最大值，直到栈顶元素$h$小于新元素$h$。

举个栗子：n=7 , 2 1 4 5 1 3 3

红色为即将弹出栈，深蓝色为已经出栈的元素，最后要插入一个虚矩形，使栈内元素全部出栈，计算最优值。

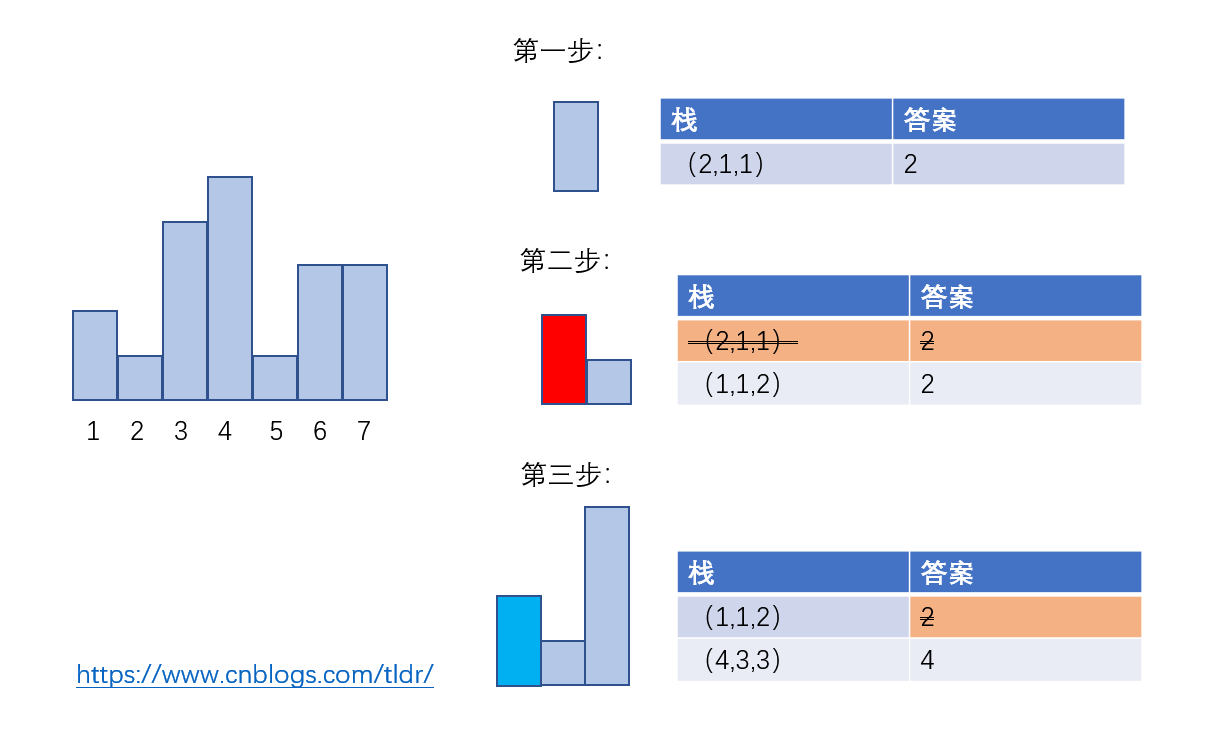
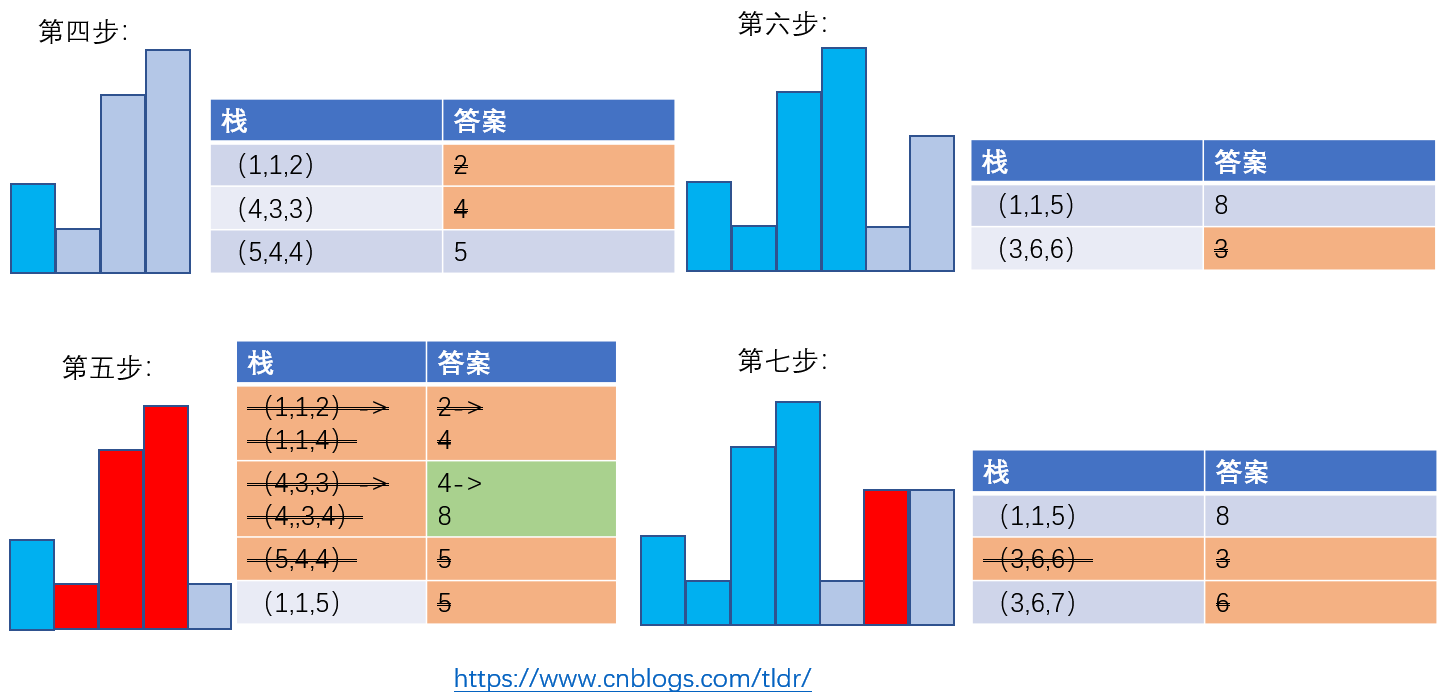
AC代码如下

#include<iostream>
#include<cstdio>
#include<stack>
#include<algorithm>
#define FOR(i,a,b) for(int i=a;i<b;i++)
#define FOR2(i,a,b) for(int i=a;i<=b;i++)
#define ll long long
#define INF  0x7f7f7f7f;
#define MAXN 100100
#define MOD 10007
using namespace std;
typedef struct{
    ll l,r,w;
}NODE;NODE nodes[MAXN];
ll arr[MAXN];
ll n,ans=0;
int main()
{
    while(cin>>n){
    if(n==0)break;
    stack<NODE>s;;ans=0;
    FOR(i,0,n)
    {
        scanf("%lld",&nodes[i].w);
        nodes[i].l=nodes[i].r=i;
    }
    nodes[n]={n,n,0};
    FOR2(i,0,n)
    {
        while(!s.empty()&&s.top().w>=nodes[i].w)
        {
            ans=max(ans,s.top().w*(s.top().r-s.top().l+1));
            nodes[i].l=s.top().l;//新元素继承出栈元素的延展性 
            ll rr=s.top().r; 
            s.pop();
            if(!s.empty())
            {//仍在栈中的元素获得延展性，计算最大值 
                s.top().r=rr;
            }
        }
        if(!s.empty())ans=max(ans,s.top().w*(s.top().r-s.top().l+1));
        s.push(nodes[i]);
    }
    printf("%lld
",ans);
    }
    
    return 0;
}

相关应用

最长上升子序列

[洛谷P1823]音乐会的等待

基本思路

此题不需要考虑元素的延展性，只需要考虑身高相等的情况，记录连续相等的人数，并累加即可

#include<iostream>
#include<cstdio>
#include<stack>
#include<algorithm>
#define FOR(i,a,b) for(int i=a;i<b;i++)
#define FOR2(i,a,b) for(int i=a;i<=b;i++)
#define ll long long
#define INF  0x7f7f7f7f;
#define MAXN 500100
#define MOD 10007
using namespace std;
typedef struct{
    ll w,sam;
}NODE;NODE arr[MAXN];
ll n,ans=0;
stack<NODE>s;
int main()
{
    scanf("%lld",&n);
    FOR(i,0,n){
        scanf("%lld",&arr[i].w);arr[i].sam=1;//自己与自己相等 
        if(s.empty()){
            s.push(arr[i]);continue;
        }
        while(!s.empty()&&s.top().w<=arr[i].w)
        {
            if(s.top().w==arr[i].w)
            {//若相等则都能见面 
                arr[i].sam+=s.top().sam;
            } 
            ans+=s.top().sam;
            s.pop();
        }
        if(!s.empty())ans++;
        s.push(arr[i]);
    }
    cout<<ans<<endl;
    return 0;
}

[洛谷P4147&BZOJ 3039]玉蟾宫

基本思路

此题可用悬线法和单调栈解决。

若用单调栈，则对每一行进行处理，表示向上延伸的高度，即$a[i][j]=ch=='F'?a[i-1][j]+1:0;$

注意末尾需要放置虚矩阵，然后逐行扫描，与SP1805 单调栈做法类似，考虑元素的延展性和单调性。

#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<stack>
#include<algorithm>
#define FOR(i,a,b) for(int i=a;i<b;i++)
#define FOR2(i,a,b) for(int i=a;i<=b;i++)
#define ll long long
#define INF  0x7f7f7f7f;
#define MAXN 2000
#define MOD 10007
using namespace std;
typedef struct{
    int w,h;
}NODE;
int n,m,arr[MAXN][MAXN];
NODE dp[MAXN][MAXN];
int main()
{
//    freopen("t1.in","r",stdin);
    cin>>n>>m;
    FOR2(i,1,n)
        FOR2(j,1,m)
        {
            char ch;
            cin>>ch;while(ch==' '||ch=='
')cin>>ch;
            dp[i][j].h=ch=='R'?0:dp[i-1][j].h+1;
        }
    FOR2(i,1,n)dp[i][m+1].h=0;
    int ans=0;
    FOR2(i,1,n)
    {
        stack<NODE>s;
        FOR2(j,1,m+1)
        {
            int temp=0;dp[i][j].w=1;
            while(!s.empty()&&s.top().h>=dp[i][j].h)
            {//使用temp记录比s.top().h小的元素通过延展可以获得的最大值 
                temp+=s.top().w;
                s.pop(); 
                if(!s.empty())ans=max(ans,s.top().h*(temp+s.top().w));
            }
            s.push(dp[i][j]);
            s.top().w+=temp;//继承比dp[i][j]大的元素的延展性 
            ans=max(ans,s.top().h*s.top().w);
        }
    }
    cout<<ans*3<<endl;
    
    return 0;
}