悬线法简介
悬线法最早由王知昆dalao在IOI2003年国家集训队论文-《浅谈用极大化思想解决最大子矩形问题》中最早提出,用于解决最大(最优)子矩阵及相关变形问题。
定义
- 有效子矩阵为内部不包含任何障碍点,且边界与坐标轴平行的子矩阵;
- 极大有效子矩阵:如果一个有效子矩阵如果不包含它且比它大的有效子矩阵,则为极大有效子矩阵;
- 最大有效子矩阵:所有有效子矩阵中最大面积的子矩阵
极大化思想
定理一
在一个有障碍点的矩形中的最大子矩阵一定是一个极大子矩阵
定理二
一个极大子矩阵的四边一定不能向外扩展,即要么每条边碰触到了障碍点或者矩形边界。
算法一
- 枚举极大子矩阵的左边界,从左到右依次扫描每一个障碍点
- 不断修改可行的上下边界,从而得出所有以这个定点为左边界的极大子矩阵
- 将点按纵坐标排序,从上到下再做同样的扫描
时间复杂度为$O(S^2)$; 当障碍点多的时候,效率比较慢。
定义2
- 有效竖线:除了俩端点外,不碰触任何障碍点的竖直线段;
- 悬线:上端点碰触障碍点或者达到矩形上端的有效竖线。
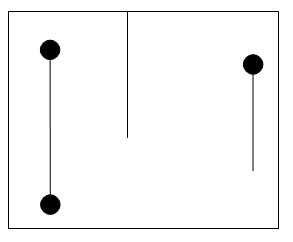
由定义2得出如下定理
定理三
将所有悬线向左右俩方向尽可能移动所得到的有效子矩阵的集合中,一定包含所有极大子矩阵。
算法二
由定理三可知,枚举所有的悬线,可以枚举出所有的极大子矩阵,时间复杂度为$O(n*m)$。
接下来,我们需要了解三个变量:悬线的高度,左移最大距离,右移最大距离。
假设对于底部为$(i,j)$的悬线,高度为$height[i,j]$,左移最大距离 为$left[i,j]$,右移最大距离为$right[i,j]$,面积为$height[i,j]*(right[i,j]-left[i,j]+1)$。
高度递推
$(i-1,j)$为障碍点,则$height[i,j]=height[i-1,j]+1$
左右边界递推
对于$left[i,j]和left[i-1,j]$,左边界始终取靠右的边界即 $left[i,j]=max(left[i,j],left[i-1,j])$;
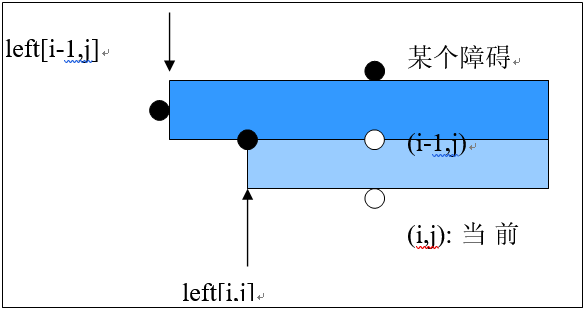
右边界同理可得 $right[i,j]=min(right[i,j],right[i-1,j])$。
洛谷P1387最大正方形
解法一:暴力

记录矩阵的前缀和,可以发现$sum{(i,j)}=(i,j)+sum{(i-1,j)}+sum{(i,j-1)}-sum{(i-1,j-1)}$。以上面的矩形为例,$(4,4)$矩阵的前缀和是$(4,3)$加上$(3,4)$减去重复的$(3,3)$加上$(4,4)$点的值。
因此枚举左上角的点$(i,j)$和边长$e$,一共是三重循环,判断前缀和的差$sum{(i+e-1,j+e-1)}-sum{(i,j)}$是否等于边长的平方$e^2$。

1 #include<bits/stdc++.h> 2 #include<iostream> 3 #include<cstdio> 4 #include<stack> 5 #include<algorithm> 6 #define FOR(i,a,b) for(int i=a;i<b;i++) 7 #define FOR2(i,a,b) for(int i=a;i<=b;i++) 8 #define ll long long 9 #define INF 0x7f7f7f7f; 10 #define MAXN 2000 11 #define MOD 10007 12 using namespace std; 13 int n,m ,arr[200][200],dp[200][200]; 14 int main() 15 { 16 cin>>n>>m; 17 FOR(i,1,n+1) 18 FOR(j,1,m+1) 19 cin>>arr[i][j]; 20 FOR(i,1,n+1) 21 FOR(j,1,m+1) 22 dp[i][j]=arr[i][j]+dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]; 23 FOR(i,1,n+1) 24 { 25 FOR(j,1,m+1) 26 cout<<dp[i][j]<<" "; 27 cout<<endl; 28 } 29 int ans=0; 30 for(int i=1;i<=n;i++) 31 { 32 for(int j=1;j<=m;j++) 33 {//枚举左上角 34 for(int e=0;e<=min(n-i,m-j);e++) 35 {//枚举边长 36 int rx=i+e-1;int ry=j+e-1; 37 if(rx>n||ry>m)break; 38 if(dp[rx][ry]-dp[i-1][ry]-dp[rx][j-1]+dp[i-1][j-1]==e*e) 39 { 40 ans=max(ans,dp[rx][ry]-dp[i-1][ry]-dp[rx][j-1]+dp[i-1][j-1]); 41 // cout<<ans<<" "<<i<<" "<<j<<" "<<e<<endl; 42 } 43 } 44 } 45 } 46 cout<<(ll)sqrt(ans)<<endl; 47 return 0; 48 }
解法二:dp
动规转移方程:
$if (a[i][j]==1) f[i][j]=min(min(f[i][j-1],f[i-1][j]),f[i-1][j-1])+1$
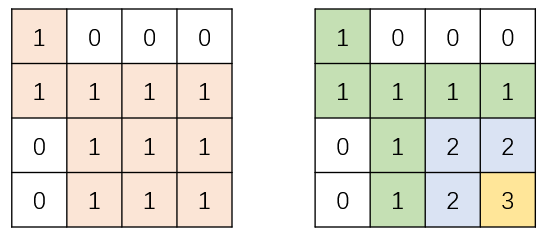
如果不懂,请看图,一个正方形的形成,最小是1,如果要扩大,则必须两边都满足自己是子正方形。
定义
- 最小的正方形:当当前格为1时,可形成最小的正方形,边长为1,面积为1;
- 子正方形:当一个正方形包含(小于或等于其边长)的正方形时,成为其含有子正方形;
定理一
每个正方形都包含子正方形,包括自己。
定理二
每个正方形的最小子正方形为最小的正方形,且每个正方形都由子正方形扩展而来
算法
如果要获得最大正方形,则由定理二可知必须由子正方形扩展而来,且必须由最小正方形扩展而来。从左上到右下,最小的正方形显而易见是单独的1,扩展的充分必要条件是在边长-1的子正方形基础上,两侧的边长都有1,即可以被扩展。

1 #include<bits/stdc++.h> 2 #include<iostream> 3 #include<cstdio> 4 #include<stack> 5 #include<algorithm> 6 #define FOR(i,a,b) for(int i=a;i<b;i++) 7 #define FOR2(i,a,b) for(int i=a;i<=b;i++) 8 #define ll long long 9 #define INF 0x7f7f7f7f; 10 #define MAXN 2000 11 #define MOD 10007 12 using namespace std; 13 int n,m,ans=0,arr[200][200],dp[200][200]; 14 int main() 15 { 16 cin>>n>>m; 17 FOR(i,1,n+1) 18 FOR(j,1,m+1) 19 { 20 cin>>arr[i][j]; 21 } 22 FOR(i,1,n+1) 23 FOR(j,1,m+1) 24 { 25 if(arr[i][j]==1)//表示可以作为正方形的右下角 26 dp[i][j]=min(min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1; 27 ans=max(ans,dp[i][j]); 28 } 29 cout<<ans<<endl; 30 return 0; 31 }
解法三:悬线法
关于初始化$l,r,up$数组
1 for(int i=1;i<=n;i++) 2 for(int j=1;j<=m;j++) 3 读入,right[i][j]=left[i][j]=j,up[i][j]=1; 4 for(int i=1;i<=n;i++) 5 for(int j=2;j<=m;j++) 6 if(满足条件) 7 right[i][j]=right[i][j-1]; 8 for(int i=1;i<=n;i++) 9 for(int j=m-1;j>=1;j--) 10 if(满足条件) 11 left[i][j]=left[i][j+1];
关于计算最优值
1 if(满足条件){ 2 right[i][j]=min(right[i][j],right[i-1][j]); 3 left[i][j]=max(left[i][j],left[i-1][j]); 4 up[i][j]=up[i-1][j]+1; 5 }
不多说,又快又准确,具体看注释

1 #include<bits/stdc++.h> 2 #include<iostream> 3 #include<cstdio> 4 #include<stack> 5 #include<algorithm> 6 #define FOR(i,a,b) for(int i=a;i<b;i++) 7 #define FOR2(i,a,b) for(int i=a;i<=b;i++) 8 #define ll long long 9 #define INF 0x7f7f7f7f; 10 #define MAXN 2000 11 #define MOD 10007 12 using namespace std; 13 int n,m,arr[MAXN][MAXN]; 14 int l[MAXN][MAXN],r[MAXN][MAXN],up[MAXN][MAXN],ans1,ans2; 15 int main() 16 { 17 cin>>n>>m; 18 FOR2(i,1,n) 19 FOR2(j,1,m)//初始化 20 cin>>arr[i][j],l[i][j]=r[i][j]=j,up[i][j]=1; 21 FOR2(i,1,n) 22 FOR2(j,2,m)//获得左边界 23 if(arr[i][j]&&arr[i][j]==arr[i][j-1]) l[i][j]=l[i][j-1]; 24 FOR2(i,1,n) 25 for(int j=m-1;j>=1;j--)//获得右边界 26 if(arr[i][j]&&arr[i][j]==arr[i][j+1])r[i][j]=r[i][j+1]; 27 FOR2(i,1,n) 28 FOR2(j,1,m) 29 { 30 // if(i>1) 31 { 32 if(arr[i][j]==arr[i-1][j]&&arr[i][j]==1) 33 {//向下扩展悬线 34 l[i][j]=max(l[i][j],l[i-1][j]);//取最右边的左边界 35 r[i][j]=min(r[i][j],r[i-1][j]);//取最左边的右边界 36 up[i][j]=up[i-1][j]+1;//高度+1 37 } 38 int a=r[i][j]-l[i][j]+1;//求宽 39 int b=min(a,up[i][j]);//求高和宽的最小值,可以构成正方形 40 ans1=max(b,ans1);//更新答案 41 } 42 } 43 cout<<ans1<<endl; 44 return 0; 45 }
洛谷P4147玉蟾宫
此题也可以用单调栈解决,详见我的另外一篇介绍单调栈的博文

1 #include<bits/stdc++.h> 2 #include<iostream> 3 #include<cstdio> 4 #include<stack> 5 #include<algorithm> 6 #define FOR(i,a,b) for(int i=a;i<b;i++) 7 #define FOR2(i,a,b) for(int i=a;i<=b;i++) 8 #define ll long long 9 #define INF 0x7f7f7f7f; 10 #define MAXN 2000 11 #define MOD 10007 12 using namespace std; 13 int n,m,arr[MAXN][MAXN]; 14 int l[MAXN][MAXN],r[MAXN][MAXN],up[MAXN][MAXN],ans=0; 15 int main() 16 {//100ms 17 cin>>n>>m; 18 FOR2(i,1,n) 19 FOR2(j,1,m) 20 { 21 char ch;cin>>ch;while(ch==' '||ch==' ')cin>>ch; 22 if(ch=='R')arr[i][j]=0; 23 else arr[i][j]=1; 24 l[i][j]=r[i][j]=j,up[i][j]=1;//读入 25 } 26 FOR2(i,1,n) 27 FOR2(j,2,m) 28 { 29 if(arr[i][j]&&arr[i][j]==arr[i][j-1]) l[i][j]=l[i][j-1]; 30 } 31 FOR2(i,1,n) 32 for(int j=m-1;j>=1;j--) 33 { 34 if(arr[i][j]&&arr[i][j]==arr[i][j+1]) r[i][j]=r[i][j+1]; 35 } 36 FOR2(i,1,n) 37 FOR2(j,1,m) 38 { 39 if(arr[i][j]&&arr[i][j]==arr[i-1][j]) 40 { 41 up[i][j]=up[i-1][j]+1; 42 l[i][j]=max(l[i][j],l[i-1][j]); 43 r[i][j]=min(r[i][j],r[i-1][j]); 44 } 45 // cout<<i<<" "<<j<<" "<<r[i][j]<<" "<<l[i][j]<<" "<<up[i][j]<<endl; 46 int size=(r[i][j]-l[i][j]+1)*up[i][j]; 47 ans=max(ans,size); 48 } 49 cout<<ans*3<<endl; 50 return 0; 51 }
洛谷P1169棋盘制作
注意此题的条件是前后相异,需要更改满足条件

1 #include<bits/stdc++.h> 2 #include<iostream> 3 #include<cstdio> 4 #include<stack> 5 #include<algorithm> 6 #define FOR(i,a,b) for(int i=a;i<b;i++) 7 #define FOR2(i,a,b) for(int i=a;i<=b;i++) 8 #define ll long long 9 #define INF 0x7f7f7f7f; 10 #define MAXN 2020 11 #define MOD 10007 12 using namespace std; 13 int n,m,arr[MAXN][MAXN]; 14 int l[MAXN][MAXN],r[MAXN][MAXN],up[MAXN][MAXN],ans1=0,ans2=0; 15 int main() 16 { 17 cin>>n>>m; 18 FOR2(i,1,n) 19 FOR2(j,1,m) 20 { 21 cin>>arr[i][j]; 22 l[i][j]=r[i][j]=j,up[i][j]=1; 23 } 24 FOR2(i,1,n) 25 FOR2(j,2,m) 26 { 27 if(arr[i][j]^arr[i][j-1])l[i][j]=l[i][j-1]; 28 } 29 FOR2(i,1,n) 30 for(int j=m-1;j>=1;j--) 31 { 32 if(arr[i][j]^arr[i][j+1])r[i][j]=r[i][j+1]; 33 } 34 FOR2(i,1,n) 35 FOR2(j,1,m) 36 { 37 if(arr[i][j]^arr[i-1][j]) 38 { 39 up[i][j]=up[i-1][j]+1; 40 l[i][j]=max(l[i][j],l[i-1][j]); 41 r[i][j]=min(r[i][j],r[i-1][j]); 42 } 43 44 int size1=(r[i][j]-l[i][j]+1); 45 // cout<<size1<<" "<<up[i][j]<<endl; 46 ans1=max(ans1,min(size1,up[i][j])); 47 int size2=size1*up[i][j]; 48 ans2=max(ans2,size2); 49 } 50 cout<<ans1*ans1<<endl<<ans2<<endl; 51 return 0; 52 }
洛谷P2701巨大的牛棚

1 #include<bits/stdc++.h> 2 #include<iostream> 3 #include<cstdio> 4 #include<stack> 5 #include<algorithm> 6 #define FOR(i,a,b) for(int i=a;i<b;i++) 7 #define FOR2(i,a,b) for(int i=a;i<=b;i++) 8 #define ll long long 9 #define INF 0x7f7f7f7f; 10 #define MAXN 2020 11 #define MOD 10007 12 using namespace std; 13 int arr[MAXN][MAXN],n,t,a,b,ans=0; 14 int l[MAXN][MAXN],r[MAXN][MAXN],up[MAXN][MAXN]; 15 int main() 16 { 17 cin>>n>>t; 18 FOR2(i,1,n) 19 FOR2(j,1,n) 20 { 21 arr[i][j]=1;l[i][j]=r[i][j]=j;up[i][j]=1; 22 } 23 FOR2(i,1,t) 24 {//读入障碍 25 cin>>a>>b; 26 arr[a][b]=0; 27 } 28 FOR2(i,1,n) 29 FOR2(j,2,n) 30 if(arr[i][j]&&arr[i][j]==arr[i][j-1]) 31 l[i][j]=l[i][j-1]; 32 FOR2(i,1,n) 33 for(int j=n-1;j>=1;j--) 34 if(arr[i][j]&&arr[i][j+1]==arr[i][j]) 35 r[i][j]=r[i][j+1]; 36 FOR2(i,1,n) 37 { 38 FOR2(j,1,n) 39 { 40 if(arr[i][j]&&arr[i][j]==arr[i-1][j]) 41 { 42 up[i][j]=up[i-1][j]+1; 43 l[i][j]=max(l[i][j],l[i-1][j]); 44 r[i][j]=min(r[i][j],r[i-1][j]); 45 } 46 int size=r[i][j]-l[i][j]+1; 47 // cout<<size<<" "<<up[i][j]<<endl; 48 ans=max(ans,min(size,up[i][j])); 49 } 50 // cout<<endl; 51 } 52 53 cout<<ans<<endl; 54 return 0; 55 }
洛谷P1578奶牛浴场
此题不能使用悬线法的解法,因为$(3*10^4)^2$的数组开不下,加上障碍点远小于$n*m$,使用极大化思想的算法一可以解决
