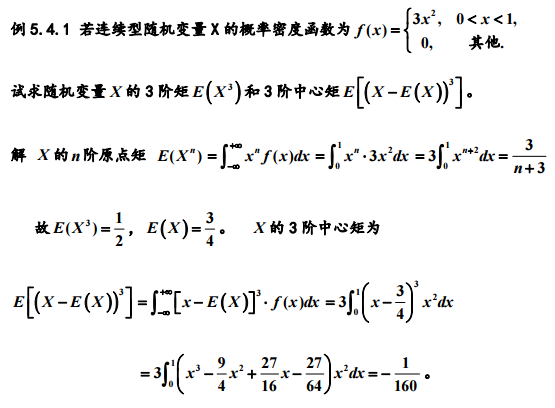1. 随机变量X的数学期望就是求加权平均值。分离散型和连续型。
期望是随机 变量的中心化特征，是随机分布的平均值。方差是随机变量对期望（平均值）偏离程度的度量。
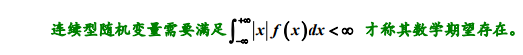
频数就是在事件发生的次数/实验的总次数。在这个定义中，就已经隐藏了大样本的条件了。
因而，期望就是在多次实验之后，你预期的结果。而不是你下一次，或者某次实验的结果。
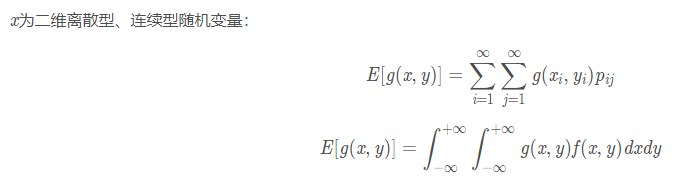
E(C)=C, E(E(X))=E(C)=C=E(X), E(cX)=c*E(X)
D(C)=0, D(CX)=C^2*D(X),
3. 方差刻画随机变量的分散程度 (方差是随机变量到期望值距离的期望)，刻画分散程度，首先要选择一个基准来刻画随机变量相对于这个基准的分散程度。 选择期望，即平均值，作为基准是合理的。用随机变量相对于期望的平均偏离程度，表达随机变量的分散程度。数学上给出的方差定义，即为X-E(X)的平方的期望。
方差反映了随机变量相对其均值的偏离程度. 方差越大, 则随机变量的取值越分散.
求方差，先求E(X)，然后代入D(X)=E(X-E(X)^2)
D(X) = E(X^2)-(E(X))^2
Var(X,Y) = E(XY)-E(X)E(Y)
方差的性质:
利用随机变量相加的期望等于随机变量的期望相加的性质，将期望展开成三项期望求和。
2E(XE(X))=2E(X)E(X)
E(X)^2是一个常数，所以E（E(x)^2）=E(x)^2，还是一个常数。
Var（aX+b）=Var（aX）=a^2Var(X)，性质：
- 随机变量加减一个常数后，只是整体上做了一个平移，其分散程度并没有任何变化所以方差应当保持不变。
- 这个公式还说明，随机变量乘以一个常数后，方差改变常数的平方倍。 这个平方关系是因为方差由相对于期望的偏差平方而定义，所以方差的单位是X的单位的平方。所以方差的平方根为随机变量的标准差。
4. 标准差：Std(X) = p D(X)
由于方差的计算中有平方， 与随机变量的量纲不同，不便于比较，所以常用标准差来作为偏离程度的数量化指标。
5. 协方差
6. 相关系数
概率统计与机器学习：期望，方差，数学期望，样本均值，样本方差之间的区别
https://blog.csdn.net/qq_33638791/article/details/74860014
1.样本均值：我们有n个样本，每个样本的观测值为Xi，那么样本均值指的是 1/n * ∑x(i)，求n个观测值的平均值
2.数学期望：就是样本均值，是随机变量，即样本数其实并不是确定的。如MSE/均方差：
PS：从概率论的角度而言：样本指的是我们现在有多少东西需要去观测，它是一种随机变量，即样本的多少是不确定的，我们得到的样本均值并不是真正意义上的期望。
3.期望：已知其观测值f（x）及其概率P，求其观测值与概率乘积的累加和，∑Xi*Pi
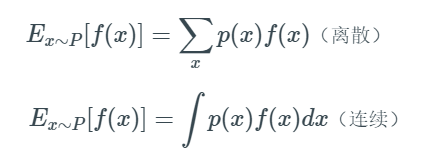
PS：期望是一种固定值，他的观测值是基于已知某几类数值及其概率，是不同于数学期望中的观测值Xi的，数学期望的观测值有一点取决于样本数量的味道，也就是求和这里的n其实是不同的
4.方差：先看一下方差的公式
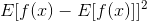
直观的说就是：观测值f(x)与其期望相减的差值的期望
换言之：方差反应的是观测值与其期望的偏差
PS：因为是与期望相减，所以这里的方差本质也是一个固定值而非随机变量
5.样本方差：
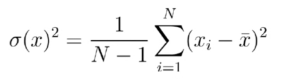
这里的观测值减去的是均值！均值的意思就是原本物质所存在的均值，即 1/n * ∑x(i)
而实际上我们可以得知方差的求解应该减去的是期望才对，其中的缘故在于我们并不能得知真正的期望是多少，
只能通过随机变量的样本求得一个近似的值来预估期望，即利用下式来证明：
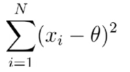， 当theta值是样本均值的时候，该式值最小（每个值减他们总和的均值）
那么同理返回样本方差的等式，上式最小意味着利用样本均值求解样本方差会把真实方差算小了
因此将N处理成N-1来增大样本方差的值
引出两个结论：
（a）当分母为N-1的时候，是我们对方差做的一个无偏估计
（b）当分母为N的时候，是我们对方差做的一个极大似然估计
做一个小总结：
- 样本均值是数学期望，求的是n个观测值的平均值，而期望指的是观测值及其概率的乘积的累加和. 在样本足够多的情况下，可以理解为样本均值趋近于期望E 即：1/n*∑x(i) ≈ ∑p(i)*x(i)
- 方差的本质是固定不变的，得到的是这个状态正儿八经与期望的偏差，而样本方差是随机变量，得到的是也是一种偏差，只不过这种偏差是对正确偏差的一种估计值。
1. 随机变量函数的分布
随机变量的函数仍然是随机变量，一般而言，随机变量经过初等函数的作用，仍然是 一个随机变量。如果我们掌握了随机变量函数的概率分布有效的计算方法，那么我 们就可以从初始分布出发，比较方便地得到新的随机变量的分布规律，而不用每个 新的随机变量的分布都从重头计算，为概率计算带来便利。我们已知的正态分布，经过线性变换变成了标准正态分布，那么X的平方会是什么样的分布特性，如果X是参数为2的指数分布随机变量，那么e的负2X次幂的分布是怎么样的？如下所示：
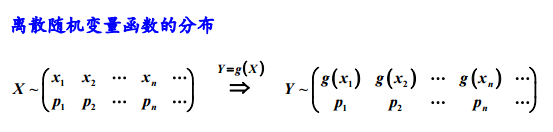
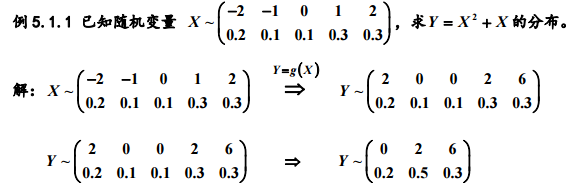
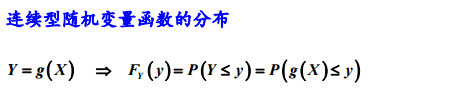
解题思路：将Y=g(X)转换成X=g(y)，再将g(y)代入解题。
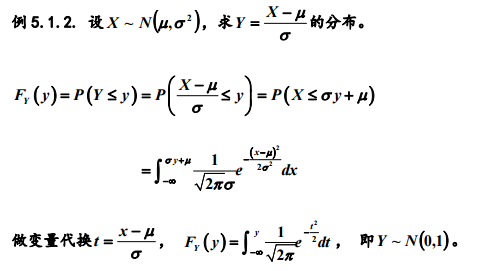
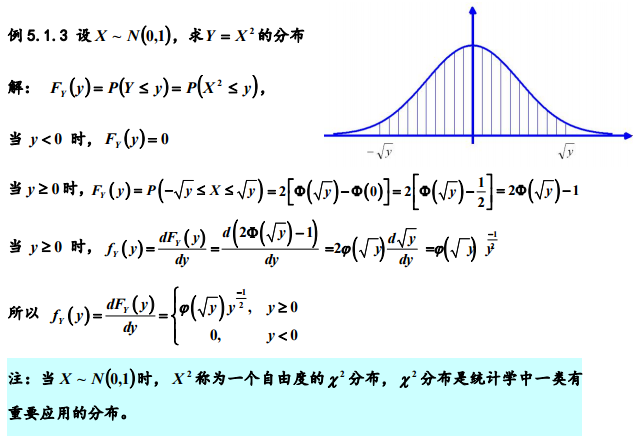
2. 随机变量的数学期望
引例：考察一射手的水平,既要看他 的平均环数是否高, 还要看 他弹着点的范围是否小。
平均环数为数学期望
弹着点范围大小说明了数据的波动的大小为方差
数学期望就是把随机变量的概率转换为求每个事件的加权平均值的方式对事件的概率进行分析。即用 “频率近似概率”的思想。期望是来源于对未来的预期。
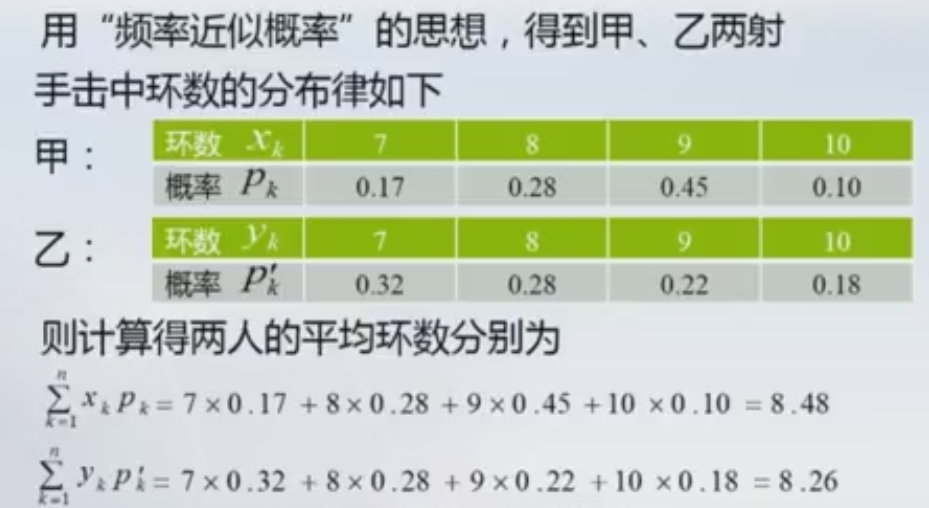
离散型随机变量X的分布律：
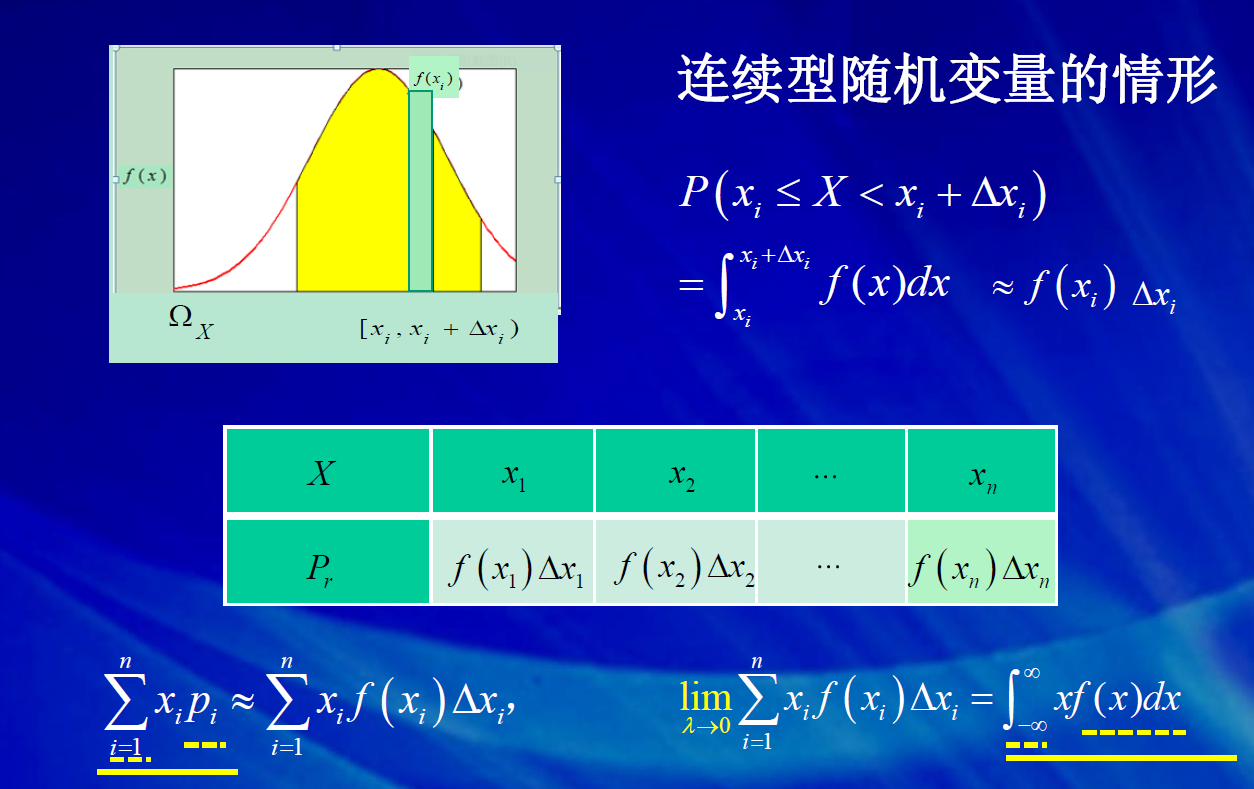
连续性随机变量X的密度函数：
备注 （1）离散型随机变量，级数和绝对收敛. （2）连续性随机变量，积分和绝对收敛.
分散的数学期望
力矩=力臂×力=∑Xk×Pk
连续的数学期望
f(x)*dx=质量，X为力臂，所以力矩=X*f(x)*dx
随机变量X的数学期望就是其加权平均值
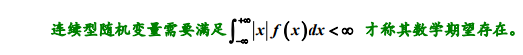
∑i = n(n+1)/2 = 6*7/2 =21
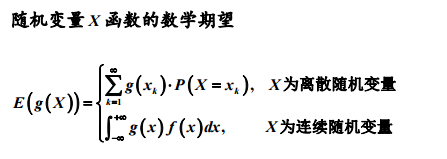
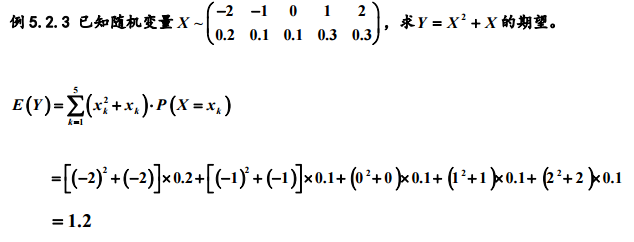
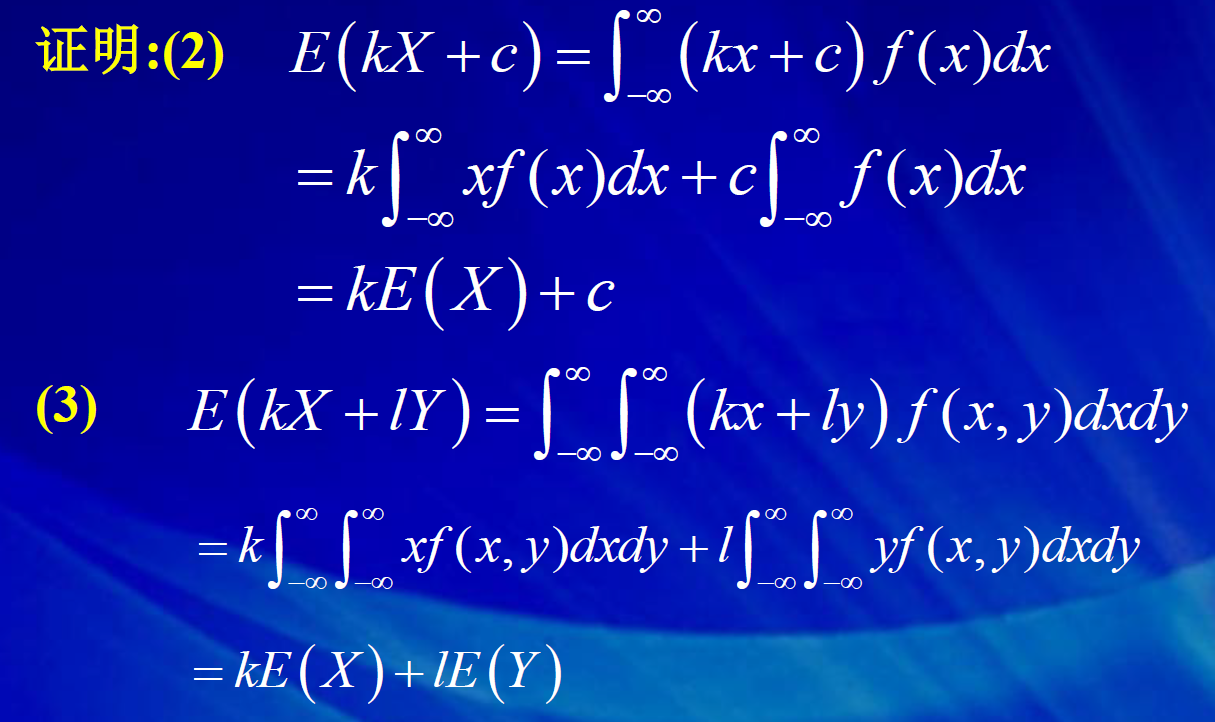
Sf(x)dx = 1; Sxf(x)dx = E(x) ; SSyf(x,y)dxdy=E(Y)
前两个结论很容易验证，后面几个关于随机变量求和的期望的结论，证明有些麻烦， 我们暂且先不加证明地引入这几个结论。
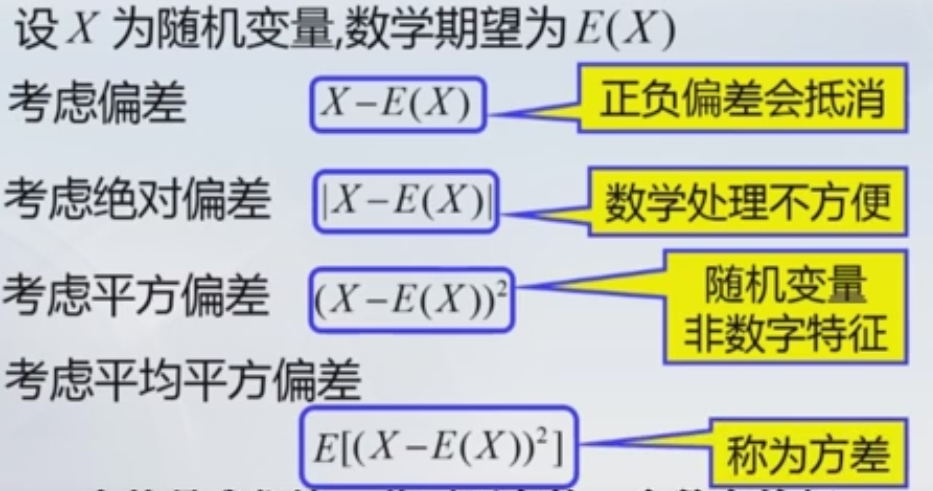
3. 随机变量的方差
方差刻画随机变量的分散程度，刻画分散程度，首先要选择一个基准来刻画随机变量相对于这个基准的分散程度。 选择期望，即平均值，作为基准是合理的。用随机变量相对于期望的平均偏离程度，表达随机变量的分散程度。数学上给出的方差定义，即为X-E(X)的平方的期望。
有时候数学期望为0，要用方差来鉴别
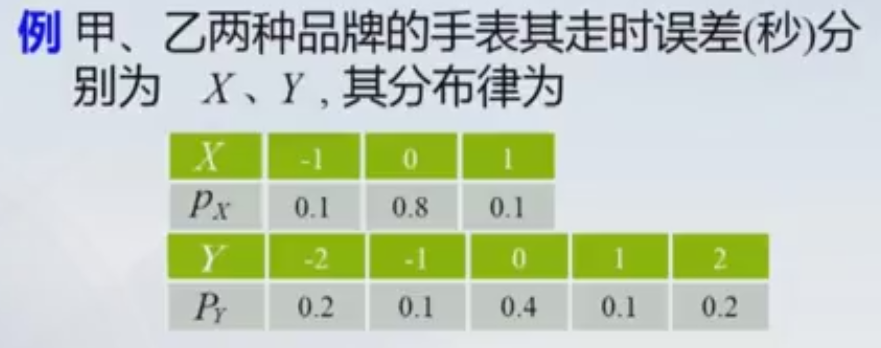
甲质量更好：甲表的准确率为80%，所以甲表的离散性更集中于0误差，而乙的正确率为40%。
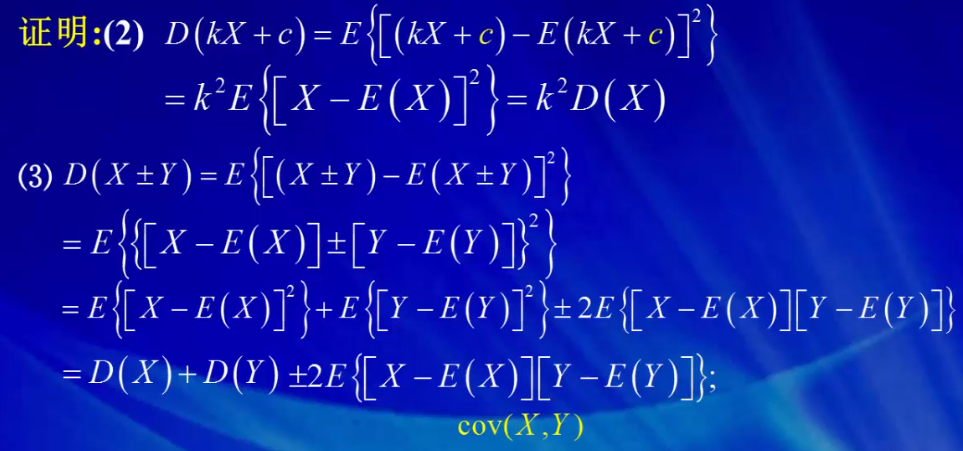
利用随机变量相加的期望等于随机变量的期望相加的性质，将期望展开成三项期望求和。
2E(XE(X))=2E(X)E(X)
E(X)^2是一个常数，所以E（E(x)^2）=E(x)^2，还是一个常数。
Var（aX+b）=Var（aX）=a^2Var(X)，性质：
1. 随机变量加减一个常数后，只是整体上做了一个平移，其分散程度并没有任何变化所以方差应当保持不变。
2. 这个公式还说明，随机变量乘以一个常数后，方差改变常数的平方倍。 这个平方关系是因为方差由相对于期望的偏差平方而定义，所以方差的单位是X的单位的平方。所以方差的平方根为随机变量的标准差。
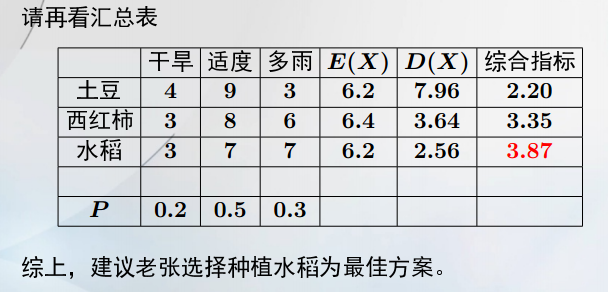
综合例子：
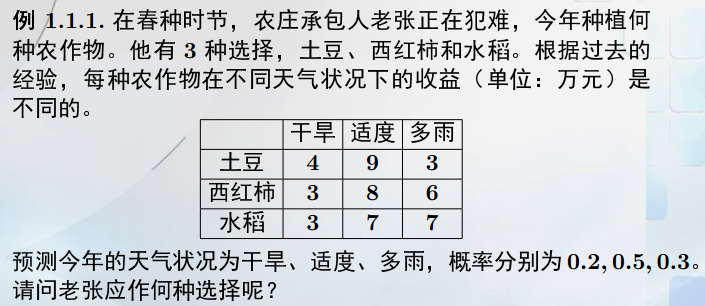
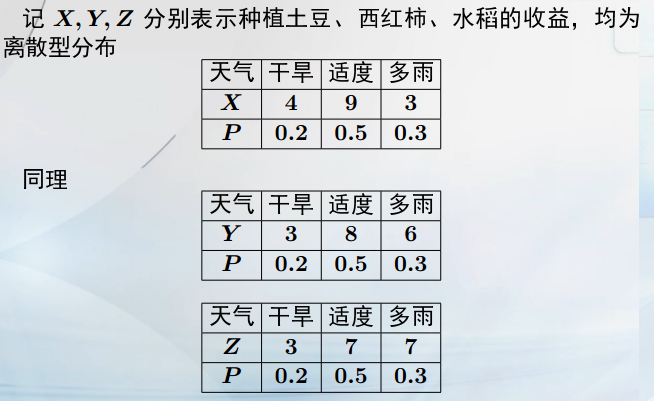
要选择期望大，且方差小的方案。但西红柿与水稻的期望，方差不同，所以引入新的综合指标标准差。
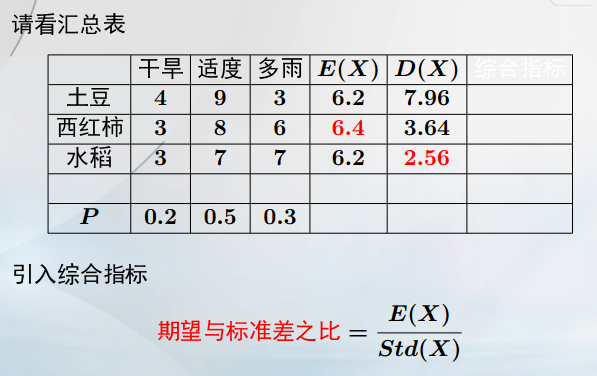
4. 原点矩与中心矩
