对于一个学不懂高深算法的小蒟蒻来说,这种暴力解法怎么能不学呢。
可惜题解中的配对堆都实用了指针,这使得像我这样的无指针选手非常头疼。
于是来来讲一讲配对堆,并给出无指针的代码。
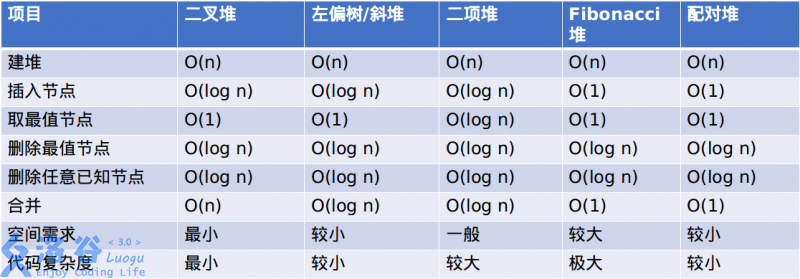
对于可并堆的比较,这张图中最显眼的便是配对堆了:
在学习配对堆之前,我们考虑用已有的知识解决这道题。
我们容易想到如果只是合并与查询最值,这仅需要一个并查集就够了。
具体来说,只需要比较大小为优先级,然后判断谁是父亲节点,这其实与并查集的启发式合并思想是异曲同工的。
现在,需要解决的难题就是如何支持删除操作。
一种暴力的想法是把这个节点的所有子节点遍历一遍,然后取优先级最高的那个节点继承他的位置。
emmm...
我们随手一个菊花图就可以把他卡掉(堆顶是菊花中心).
考虑在这时候把这个堆搞成一个比较利于我们操作的形态。
其实有很多种方法,这里介绍两种。
第一种就是首先把相邻的两个节点合并成一个,然后把所有的合并到最后那一个去。(当然合并时还是按照优先级选根)
第二种方法是每次去除两个子节点,合并后当做一个新的子节点继续和其他的的合并。
你会问:这两种方法不都是 (mathcal O(n)) 的吗?
诚然,但是我们在维护合并子节点时悄悄把这种不利的结构改成了分叉少的有利结构,我也不知道怎么证明,均摊是 (mathcal O(log n)) 的。
反正能过就行了(
那如何去维护子节点这一操作呢?
我们考虑到在合并时维护即可,容易用前向星/邻接表来存储。
因为是确定方向的有根树,所以采用有向图存边。
为什么删除节点时不用删除边?
因为删除的节点不会再用到去遍历出边,所以这些边废弃了,你也不用管。
容易看出合并的操作无论你怎么玩都是 (mathcal O(1)) 的,十分优秀。
于是你就学会了配对堆。
下面给出无指针有注释的代码(重建树根使用了较好写的第二种方式):
#include"iostream"
#include"cstdio"
#include"cmath"
using namespace std;
#define read(x) scanf("%d",&x)
#define MAXN 100005
int n,m;
int f[MAXN],val[MAXN];
int t,x,y;
struct node
{
int to,nxt;
}e[MAXN<<1];//因为要重复加边,所以最好要开大一些(虽然不开也过了)
int head[MAXN],cnt=0;
int le[MAXN];
void add(int u,int v){e[++cnt].to=v,e[cnt].nxt=head[u],head[u]=cnt;}
int getf(int u){return f[u]=(f[u]==u)?u:getf(f[u]);}
int merge(int u,int v)
{
int t1=getf(u),t2=getf(v);
if(t1==t2) return 0;
if(val[t1]>val[t2]||(val[t1]==val[t2]&&t1>t2)) swap(t1,t2);
//维护优先级(数字大小,序号)
f[t2]=t1,add(t1,t2);//加边
return t1;
}
void del(int u)
{
int lst=0;
for(int i=head[u];i;i=e[i].nxt)
{
int j=e[i].to;
f[j]=j;
if(!lst) lst=j;//更新现在的根
else lst=merge(lst,j);
}
f[u]=lst;//此处十分重要,为了在找根的时候方便,将原来根的父亲设为现在的根,相当于修改了所有节点的根
return;
}
int main()
{
read(n),read(m);
for(int i=1;i<=n;i++) read(val[i]),f[i]=i,le[i]=1;
//le[]数组用来维护是否存在
for(int i=1;i<=m;i++)
{
read(t),read(x);
if(t==1)
{
read(y);
if(le[x]&&le[y]) merge(x,y);
}
else
{
int op=getf(x);
if(!le[x]) printf("-1
");
else
{
printf("%d
",val[op]);
le[op]=0;
del(op);
}
}
}
return 0;
}