Lecture 9:Linear Regression
9.1 Linear Regression Problem

图 9-1
现在用机器学习来决定给用户信用卡的额度。如图 9-1 所示,输入的是一系列用户相关的特征,输出的是信用卡额度。本例采用 Linear Regression
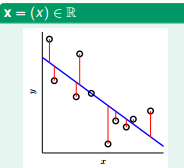
图 9-2 2D Linear Regression
如图 9-2 所示,一般用距离的平方来评估 Regression 的误差。对于 N Dimension 的 Linear Regression, Ein 如图 9-3 所示
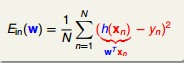
图 9-3
现在的问题就是如何 Minize Ein(W)?
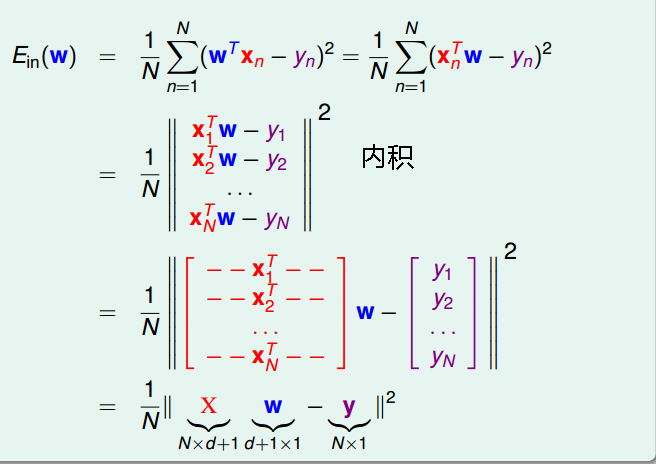
图 9-4
如图 9-4 所示, 推导出的 Ein 是凸函数。在导数为 0 的是可以取到 mini value
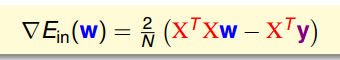
图 9-5
此时,要分二种情况。一种是 XTX invertible (often but not always), 则可以取到 unique W。否则 W 有很多解

图 9-6
9.2 Linear Regression Algorithm
y = Xw 和 wLIN = X+y 带入到公式 9-1, 可以得出如图9-7 所示的结论
$$ E_{in}(W_{LIN}) = frac{1}{N}Vert y - hat{y} Vert^2 $$

图 9-7
9.3 Generalization Issue
Ein 的均值有个特殊的表达式,如图 9-8 所示。我们不做证明,简单想象一下,假设数据集是线性可分的,我们将样本空间中的所有数据都用计算 Ein。 Ein 的表达式肯定是和 Noise level 有关的(参考第八节课关于 Nosie 的定义)。
这样我们就可以接受图 9-8 的中表达式
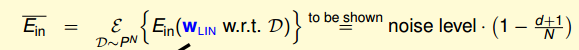
图 9-8
现在我们来从思考图 9-7 中 ÿ (不知道怎么打出 y hat 字符~)的几何意义。从下面的公式可以看出最终的 ÿ 由 y 的线性组合加上某个 ⊥ y 所在平面的向量 (如何没有这个 ⊥向量,Ein 就能等于0 如果你的计算资源足够多)。
求解 ÿ 的过程也等于是求 ⊥ 平面向量的过程。
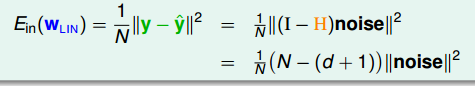
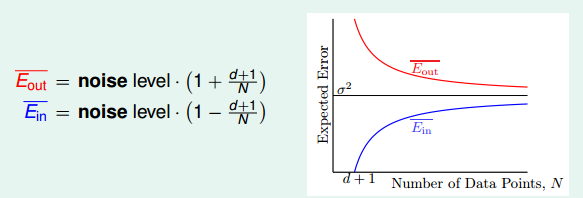
图 9-9 图 9-10
课件中在讨论几何意义时,也顺便了证明了 图9-9所示的结论。在前面的笔记中就贴出了类似图 9-10 的图片,当时没有做过多的解释
记得 VC Bound 是有关 in-sample 和 out-sample Error 的公式,图 9-10 是也是关于 in-sample 和 out-sample Error。后续的笔记还有 in-sample 和 Augment Error 关系
9.4 Linear Regression for Binary Classification
Linear Classification 的 Ein 很难 minized(不可导,不能用现有的方法), Linear Regression 的 Ein 很容易被优化。
而且图 9-11 所示,Lineare Regression 的损失函数要大于 Linear Classification 所以可用 LIneare Regression 来做分类

图 9-11
最好要贴上本章最有一页截图

图 9-12
题外话:
T1:先看图 9-12, 图 9-12 是第十三节讨论 Noise 时展示的 in-sample 和 out-sample 的 Nosie Level。
结合图 9-12 和图 9-10 这两张图,不知道大家有没有发现有个好玩的东西?下面我来讲一下我发现的好玩的东西:
1. 图 9-10 和 图 9-12 很像
2. 图 9-10 所示结论是针对 Linear Regression 得出的,且这个结论要借助 Linear Regession 解析解的几何意义(即 最佳的 ÿ 等于⊥ x span 的向量 Plus x span 内一个向量)来证明。
3. 图 9-12 则是截取于第十三节,对所有算法都成立(基本上吧),不局限于 Linear Regression。那么图 9-12 中的结论是不是很有趣,是不是也有类似 Linear Regression 的几何意义? 是不是也有 矩阵 trace 迹?

图 9-12 十三节 Noise