归并排序
一.概述
这里归并的含义将两个或两个以上的有序表组合成一个新有序表,本文讲述二路归并排序。
二、排序过程
- 初始序列看成n个有序子序列,每个子序列长度为1
- 两两合并,得到(n/2向下取整数)个长度为2或1的有序子序列
- 再两两合并,重复直至得到一个长度为n的有序序列为止
二路归并排序主旨是“分解”与“归并”
分解:
1.将一个数组分成两个数组,分别对两个数组进行排序。
2.循环第一步,直到划分出来的“小数组”只包含一个元素,只有一个元素的数组默认为已经排好序。
归并:
1.将两个有序的数组合并到一个大的数组中。
2.从最小的只包含一个元素的数组开始两两合并。此时,合并好的数组也是有序的。
1.将两个顺序表合并成一个有序表
首先我们来看看两个顺序表是如何变成一个有序表的,实际上做法就是将两个指针指向两个数组,然后进行比较,看那个指针指向的数据小,将小的数据插入新的数组里,然后将这个指针加1.如图所示。
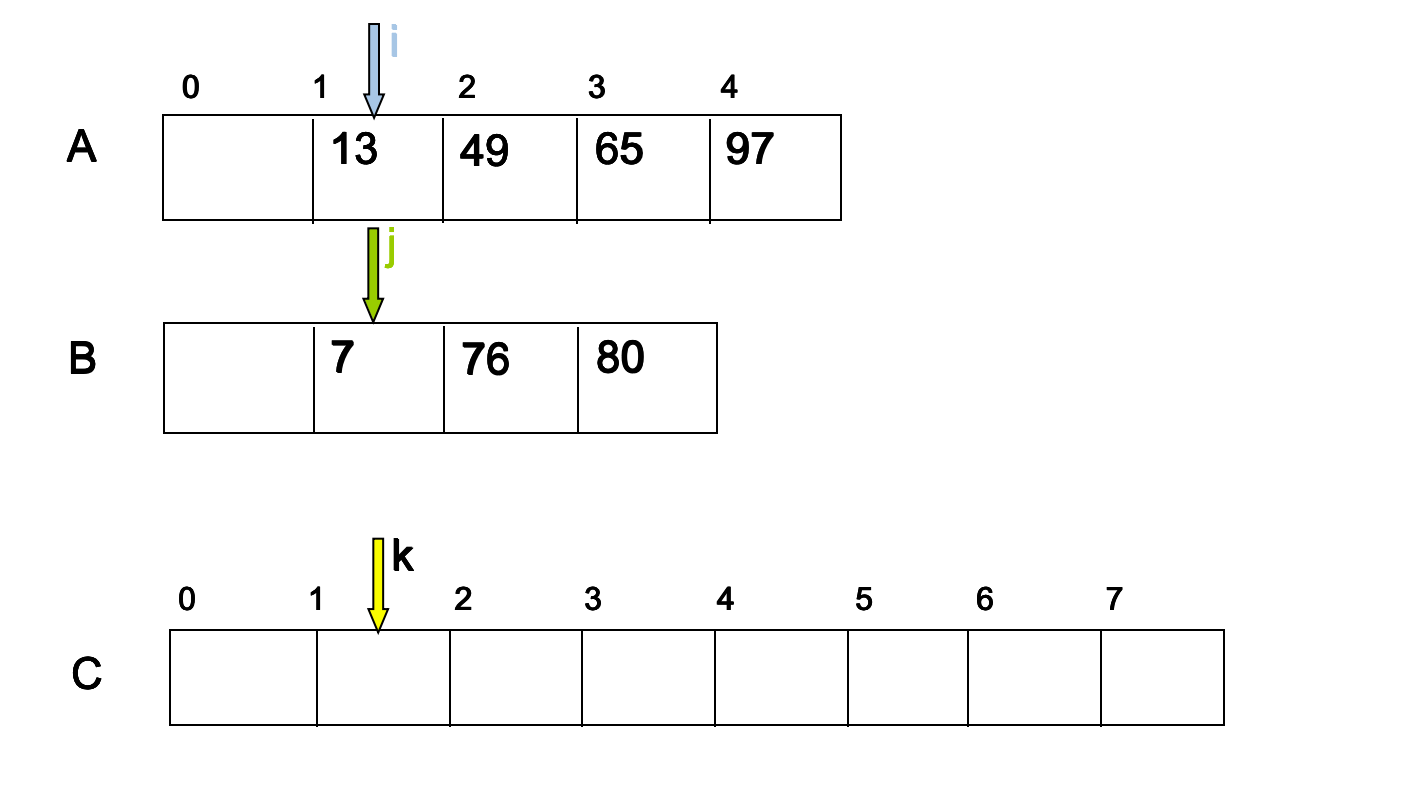
代码如下:
int [] mergeSort(int a[] , int b[],){
int c[a.length + b.length] ;
int i = 0;
int j = 0;
int k = 0;
while (i < a.length && j < b.length){
if ( a[i] < b [j]){
c[k ++] = a[i];
i ++;
}else{
c[k ++] = b[j];
j++;
}
}
while ( i < a.length ){
c[k] = a [i];
i ++;
k ++;
}
while ( j <b .length ){
c[k] = a [j];
j ++;
k ++;
}
return c;
}
2.过程
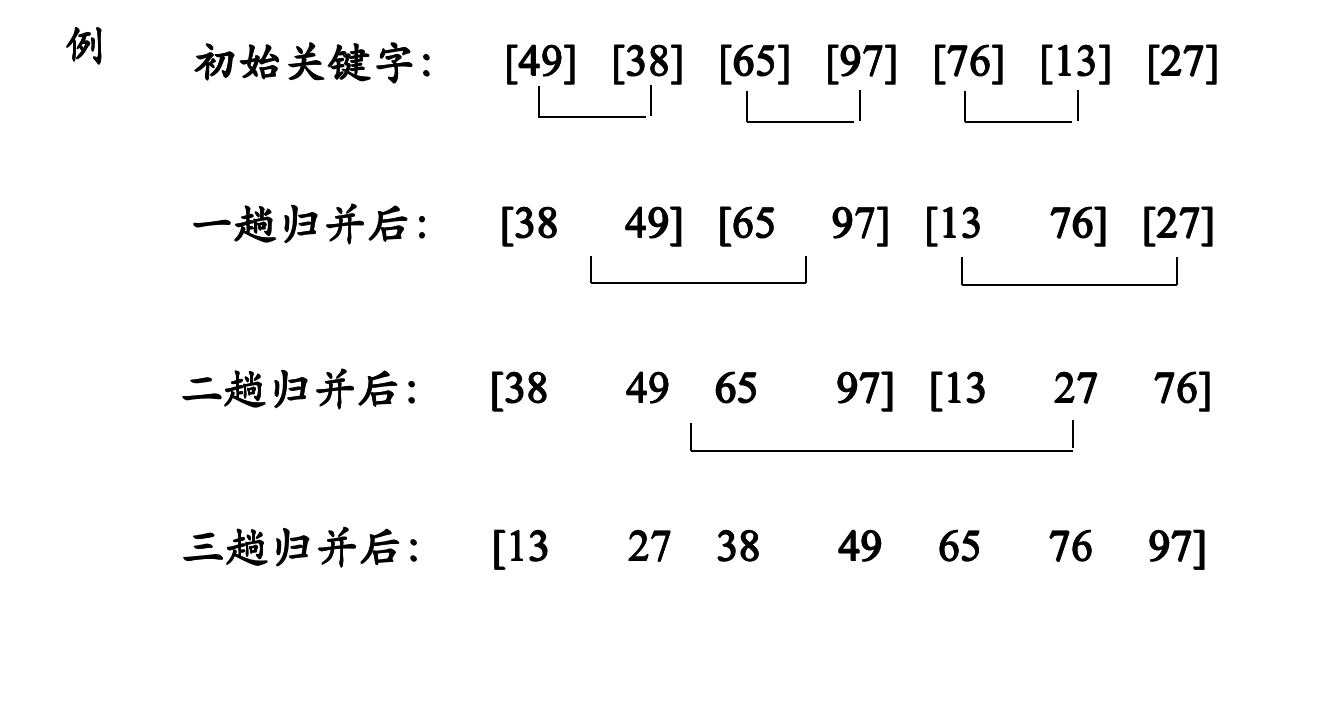
可以看出这个过程,每次两两进行比较的时候,都可以表示是两个有序的数组,变成一个有序数组的过程。经过数次的变化,就好变成排序状态的数组。
三.算法分析
时间效率:$O(nlog_2n) (
空间效率:)O(n)$
稳 定 性:稳定
四.完整代码
public class MergeSort {
public static int[] sort(int[] nums, int low, int high) {
int mid = (low + high) / 2;
if (low < high) {
// 左边
sort(nums, low, mid);
// 右边
sort(nums, mid + 1, high);
// 左右归并
merge(nums, low, mid, high);
}
return nums;
}
public static void merge(int[] nums, int low, int mid, int high) {
int[] temp = new int[high - low + 1];
int i = low;// 左指针
int j = mid + 1;// 右指针
int k = 0;
// 把较小的数先移到新数组中
while (i <= mid && j <= high) {
if (nums[i] < nums[j]) {
temp[k++] = nums[i++];
} else {
temp[k++] = nums[j++];
}
}
// 把左边剩余的数移入数组
while (i <= mid) {
temp[k++] = nums[i++];
}
// 把右边边剩余的数移入数组
while (j <= high) {
temp[k++] = nums[j++];
}
// 把新数组中的数覆盖nums数组
for (int k2 = 0; k2 < temp.length; k2++) {
nums[k2 + low] = temp[k2];
}
}
}
参考 :
https://www.cnblogs.com/horizonice/p/4102553.html
《数据结构》 严蔚敏
《算法导论》2.1章节