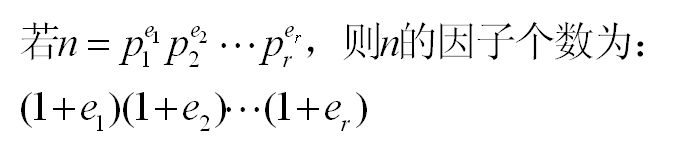zoj 3286 Very Simple Counting---统计[1，N]相同因子个数

Very Simple Counting

---

Time Limit: 1 Second      Memory Limit: 32768 KB

---

Let f(n) be the number of factors of integer n.

Your task is to count the number of i(1 <= i < n) that makes f(i) = f(n).

Input

One n per line (1 < n <= 1000000).

There are 10000 lines at most.

Output

For each n, output counting result in one line.

Sample Input

4
5

Sample Output

0
2

Hint

f(1) = 1, f(2) = f(3) = f(5) = 2, f(4) = 3.

---

Author: WU, Jun
Source: ZOJ Monthly, December 2009

理论依据：

zoj的题目，对时间和空间的要求都很高。

这一题，首先做的时候，超时。

不看时间，不看数据，直接枚举，不超时是不可能。

根据的公式和上一题福州大学oj那一题是一样的。

贴一下超时代码吧，留个纪念。

//超时代码

#include<stdio.h>
#include<stdlib.h>

int f[1000003];
int Num_Euler(int n)
{
    int num=1,k,i;
    for(i=2;i*i<=n;i++)
    if(n%i==0)
    {
        k=1;
        while(n%i==0)
        {
            k++;
            n=n/i;
        }
        num=num*k;
    }
    if(n!=1)
    num=num*2;
    return num;
}

void make_ini()
{
    int i;
    for(i=1;i<=1000000;i++)
    f[i]=Num_Euler(i);
}
int main()
{
    int n,i,num;
    make_ini();
    while(scanf("%d",&n)>0)
    {
        num=0;
        for(i=1;i<n;i++)
        if(f[i]==f[n])
        num++;
        printf("%d
",num);
    }
    return 0;
}

后来想用筛选法来筛一次，然后求值。第一次写的时候，也错了。

void make_NumEuler()
{
    int i,j,k;
    for(i=1;i<=1000000;i++)
    opl[i]=1;
    for(i=1;i<=len;i++)
    for(j=prime[i],k=2;j<=1000000;j=j+prime[i],k++)
    opl[j]=opl[j]*k;
}

思路是有的，就是没有写出来，(⊙o⊙)…
最后的代码：

#include<iostream>
#include<map>
#include<cstdio>
#include<cstdlib>
#include<cstring>

using namespace std;


bool  s[1000003];
int num[1000003];
int ans[1000003];//个数
int   f[1000003];
map<int,int>Q;


void make_ini()
{
    int i,j,k;
    for(i=1;i<=1000000;i++)
    {
    num[i]=i;
    ans[i]=1;
    f[i]=0;
    }
    for(i=2;i<=1000000;i++)
    if(s[i]==false)//是素数
    {
        for(j=i;j<=1000000;j=j+i)//枚举每个素数的倍数
        {
           // if(j%i==0) //这个肯定成立，不需要
            {
                k=1;
                while(num[j]%i==0)
                {
                    num[j]=num[j]/i;
                    k++;
                }
                ans[j]=ans[j]*k;
            }
            s[j]=true;
        }
    }
    for(i=1;i<=1000000;i++)
    {
        k=ans[i];
        if(Q.find(k)==Q.end())
        {
            Q[k]=1;
        }
        else Q[k]++;
        f[i]=Q[k];
    }
}

int main()
{
    int n;
    make_ini();
   // Q.clear();
    while(scanf("%d",&n)>0)
    {
        printf("%d
",f[n]-1);
    }
    return 0;
}