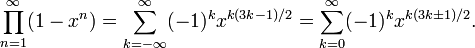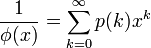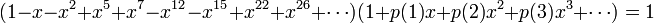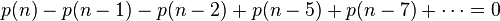五边形数定理
转自《维基百科》 http://zh.wikipedia.org/wiki/五邊形數定理
五边形数定理是一个由欧拉发现的数学定理,描述欧拉函数展开式的特性[1] [2]。欧拉函数的展开式如下:
亦即
欧拉函数展开后,有些次方项被消去,只留下次方项为1, 2, 5, 7, 12, ...的项次,留下来的次方恰为广义五边形数。
若将上式视为幂级数,其收敛半径为1,不过若只是当作形式幂级数(formal power series)来考虑,就不会考虑其收敛半径。
和分割函数的关系
其中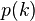 为k的分割函数。
为k的分割函数。
上式配合五边形数定理,可以得到
考虑 项的系数,在 n>0 时,等式右侧的系数均为0,比较等式二侧的系数,可得
项的系数,在 n>0 时,等式右侧的系数均为0,比较等式二侧的系数,可得
因此可得到分割函数p(n)的递归式
以n=10为例
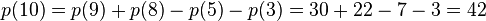
- 这样就能在log(n)的时间下得到p(n)的值。