COCI 2020/2021 CONTEST #5 解题报告

Magenta

考虑 ( ext{Subtask 2})，即所有边都是品红边的情况。显然 ( ext{Paula}) 赢仅当 ( ext{dist}(a,b)) 为偶数，( ext{Marin}) 赢仅当 ( ext{dist}(a,b)) 为奇数。

现在回到一般情况。我们发现在一般情况下，区别于 ( ext{Subtask 2})，还有两种情况需要讨论：( ext{Paula}) 无法移动到邻近节点或 ( ext{Marin}) 无法移动到邻近节点。这两种情况分别是 ( ext{Marin}) 获胜和 ( ext{Paula}) 获胜。并且在必胜的情况下，也可能会存在必输的一方躲进必胜的一方无法进入的一个连通块，因此必胜的一方可能获胜 (/) 平局。判断一下这种情况即可。

设可能必输的一方初始节点为 (A)，可能必胜的一方初始节点为 (B)（还可能平局），则必输的一方只可能到达那些 ( ext{dist}(A,z)< ext{dist}(B,z)) 的节点，因为必胜的一方一定能够先于必败的一方到达那些 ( ext{dist}(A,z)geq ext{dist}(B,z)) 的节点。如果必输的一方在上述条件下能够到达一条边 (x o y) 的两个端点，且必胜的一方无法到达，则一定会达成平局。否则必胜方能够取得胜利。

证明一下必胜方在加入蓝边和红边后采取最优策略最劣仍然能够达成平局。同 ( ext{Subtask 2})，并且如果一方卡在某个节点无法前进，他会反复横跳，直到另一方与他相邻。即被追赶的并不会成为追赶方，不会有反杀的情况。

Planine

考虑 ( ext{Subtask 1})，显然可以对于每一个山谷求出最左和最右的可覆盖点。如下图：

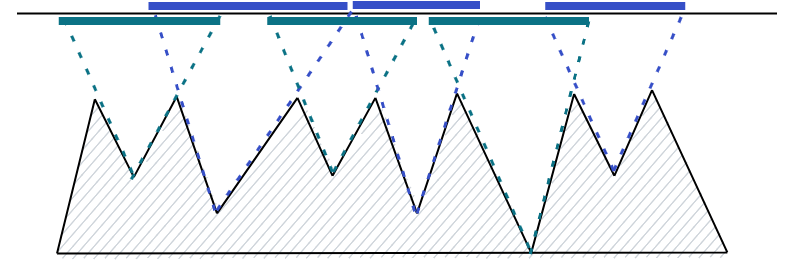
这就转化成了一个经典问题，求最少点数覆盖 (m) 条线段。可以使用贪心在 (O(nlog n)) 内解决这个问题。

但是对于山峰高度不相同的情况，我们并不能这样做。因为可能会出现一种情况，使得与当前山谷不相邻的山峰遮挡掉了光源。如：

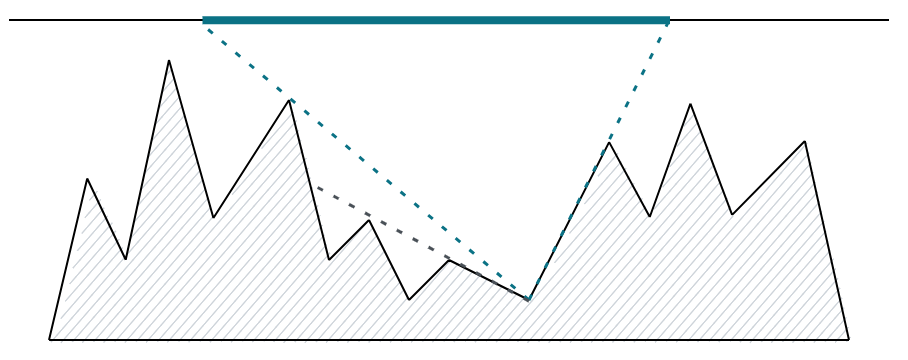
尽管在一般情况下，上面的做法并不可行。但这种转化问题的方法是非常好的，我们试着去求出一个光源可以照射到当前山谷的区间，就可以继续沿用这种做法。

这里先讨论求区间左边界。我们发现，如果将当前山谷的点 (x) 加入之前山峰构成的上凸包中，则凸包倒数第二个点 (z) 的山可能会遮挡掉光源。为什么是上凸包呢？因为上凸包中不保留那些一定不会遮挡掉光源的边。之所以是倒数第二个点 (z)，是因为 (z) 之前某个点 (y) 与 (x) 的连线若小于 (x,z) 连线的斜率，则定会被遮挡掉。证明可以参考上凸壳定义。而在光源不被遮挡掉的情况下，我们希望 (y=h) 直线上光源 (A) 与点 (x) 的连线中，斜率尽可能小。自然取斜率为 (x,z) 连线的时候最优。

求区间右边界也是一样的。不过是反着做一遍，但需要注意反着做的时候，(x) 坐标变为降序，因此斜率也会相应取反，此处应求下凸包。不懂的话手玩一下就可以理解了。

Sjeckanje

手玩一下，可以发现被划分出的段一定都是单调的。因为如果一个被划分出的段不是单调的，可以再继续划分，这样会使得答案更优。这样我们就有了一个 (O(n)) 的 ( ext{DP})，询问时每次暴力修改 ([l,r])，可以达到 (O(qn))。但这远远不够，我们尝试来挖掘更多性质。

套路的，我们将极差拆成一些差分之和。例如序列 ([3,5,6,7]) 的极差为 (7-3=4)，可以写作 ((5-3)+(6-5)+(7-6)=4)，再比如序列 ([13,11,7,5]) 的极差为 (13-5=8)，也可以写作 ((13-11)+(11-7)+(7-5)=8)。对于不知道这个套路的，这里简要说明一下。通过差分和约去中间运算，只得到最大值减去最小值是这种套路的原理。我们发现，第二种序列处理极差似乎就是第一种序列处理极差的相反数。于是可以总结为，对于一个单调序列([a_1,a_2,a_3,a_4...a_m]) 其极差为 (|a_1-a_2|+|a_2-a_3|+|a_3-a_4|+...|a_{m-1}-a_{m}|)。

有了这个结论，我们尝试将它应用到序列划分过程中。记 (d_i=a_i-a_{i+1})，则问题转化为选取一些 (d_i)，令 (sum |d_i|) 最大，且不能够同时选择的 (d_x) 与 (d_{x+1})，使得 (d_x imes d_{x+1}<0)。换句话说，选取的相邻 (d_i) 不能够是一正一负的。可以来证明一下，根据差分的定义，(d_x=a_x-a_{x+1},d_{x+1}=a_{x+1}-a_{x+2})，而 (a_{x+1}) 显然是不能够被同时计入两个单调性相反的序列中的。

于是想到使用简单的 ( ext{DP}) 来解决转化后的问题。设 (f_{x,0/1}) 为前 (x) 个元素，第 (x) 个元素选 (/) 不选能够取到的最大值。能够得到转移方程：

[f_{x,0}=max(f_{x-1,0},f_{x-1,1}) \ f_{x,1}=max(f_{x-1,0},f_{x-1,1}+(-infty) imes[d_x imes d_{x-1}< 0])+d_x ]

注意到区间加在差分数组上是两个单点加。但是这样的一个 ( ext{DP}) 似乎并不便于处理修改。我们考虑将它变为一个任意的区间 ( ext{DP})，这样就可以套路的使用线段树维护区间 ( ext{DP})。设 (f_{l,r,0/1,0/1}) 为 (iin[l,r],sum |d_i|) 在 (l) 处取 (/) 不取，在 (r) 处取 (/) 不取，能够取到的最大值。

转移方程为：

[f_{l,r,x,y}=max{f_{l,i,x,0}+f_{i+1,r,0,y},f_{l,i,x,1}+f_{i+1,r,0,y},f_{l,i,x,0}+f_{i+1,r,1,y}} \ ext{if } d_{i} imes d_{i+1}geq 0,f_{l,r,x,y}=max(f_{l,r,x,y},f_{l,i,x,1}+f_{i+1,r,1,y}) ]

初值：

[f_{i,i,0,1}=f_{i,i,1,0}=-infty,f_{i,i,0,0}=0,f_{i,i,1,1}=d_i ]

修改时根据转移方程和初值对应维护即可。时间复杂度为 (O(n+qlog n))。