
线性dp问题
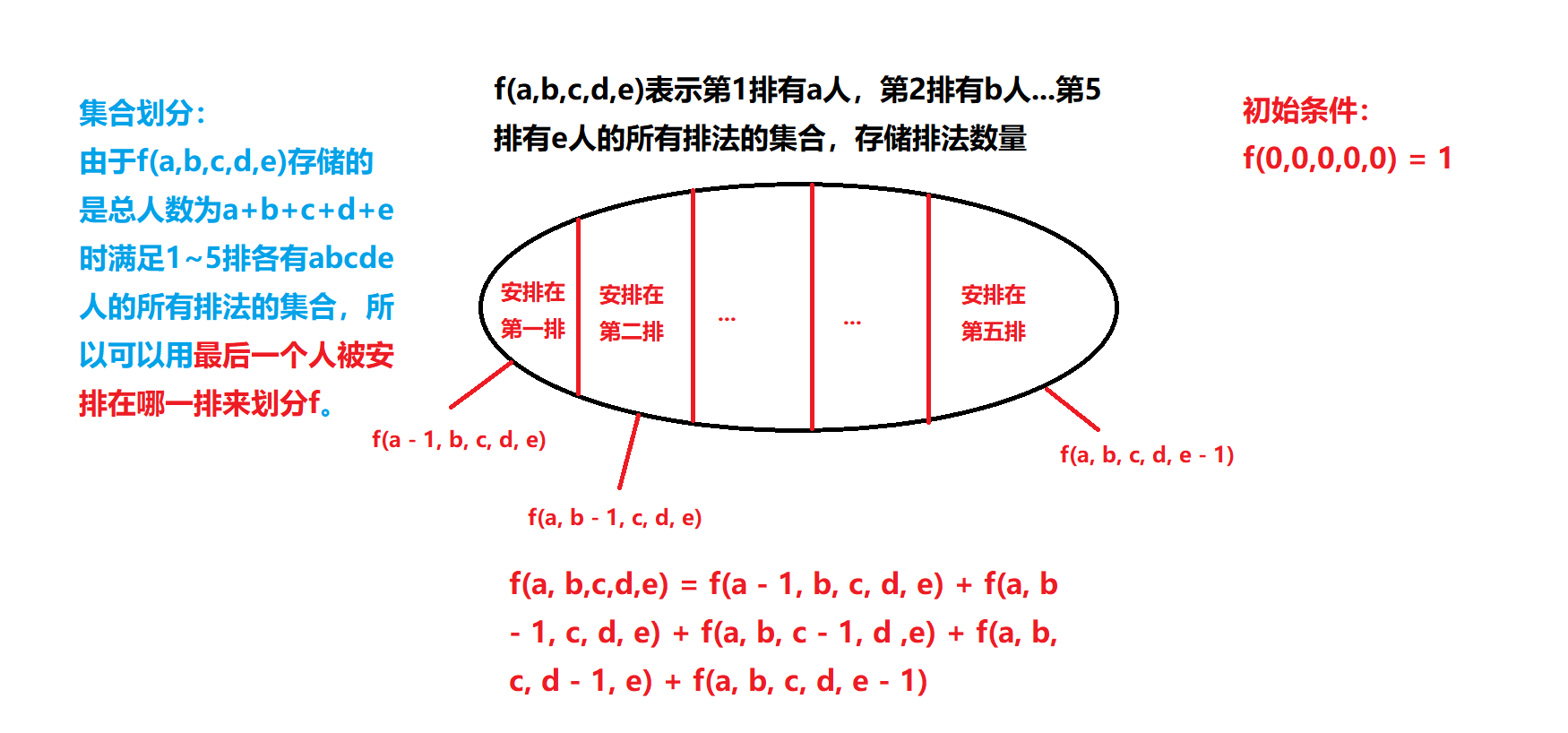
答案就是(f(N_1, N_2, N_3, N_4, ..., N_{max})),max是行数的最大值,此题的max为5
下面举一个阵列的例子,并分析为什么是dp,状态怎么设计,状态怎么枚举,合法状态和非法状态

复杂度:由于最多30人,由乘法原理,总状态数为每一行的人数的可能情况的乘积,所以每一行6人的情况的状态数最多为(7^5),而每一个状态的计算需要用到5个状态,所以总的计算量=(7^5 * 5 = 84035), 多组再乘一个T
#include<iostream>
#include<cstring>
using namespace std;
const int N = 31;
#define LL long long
LL f[N][N][N][N][N];
int k;
int main(){
while(cin >> k, k){
memset(f, 0, sizeof f);
int s[5] = {0}; // 必须初始化为0
for(int i = 0; i < k; i ++) cin >> s[i];
f[0][0][0][0][0] = 1;
for(int a = 0; a <= s[0]; a ++)
for(int b = 0; b <= min(a, s[1]); b ++)
for(int c = 0; c <= min(b, s[2]); c ++)
for(int d = 0; d <= min(c, s[3]); d ++)
for(int e = 0; e <= min(d, s[4]); e ++){
LL &v = f[a][b][c][d][e];
if(a - 1 >= b) v += f[a - 1][b][c][d][e];
if(b - 1 >= c) v += f[a][b - 1][c][d][e];
if(c - 1 >= d) v += f[a][b][c - 1][d][e];
if(d - 1 >= e) v += f[a][b][c][d - 1][e];
if(e) v += f[a][b][c][d][e - 1];
}
cout << f[s[0]][s[1]][s[2]][s[3]][s[4]] << endl;
}
return 0;
}