题意:给你一个含有n个结点的树(无向无环图,这个条件非常重要),判断能否按照每组k个结点,将其分成n/k组,并且要求每组仍然连通
结论:如果一个树可以被分成满足以上条件的组,那么从任意一个点出发(以任意一个结点为根)都可以将树按照上面的条件分块,并且分法唯一
将树按照无向图存储(保证任意一个结点都可以作为根,从他出发可以到达树上的任意一个结点),然后选择1号结点作为根递归求以每一个结点为根的子树大小,每当计算得到的子树大小为k时,说明找到了一组,此时令他向上一层返回的值为0,表示它的双亲结点不能和他再组合了,即他对它的双亲结点的数目贡献为0。
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int N = 100010;
int h[N], e[N << 1], ne[N << 1], idx;
int T;
int n, k, g;
int cnt[N];
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int dfs(int u, int v){
int sum = 1;
for(int i = h[u]; i != -1; i = ne[i]){
int j = e[i];
if(j != v) sum += dfs(j, u);
// 此处不同
if(sum == k){
g ++;
return 0;
}
}
return sum;
}
int main(){
cin >> T;
while(T --){
memset(h, -1, sizeof h);
idx = 0;
g = 0;
cin >> n >> k;
for(int i = 0; i < n - 1; i ++){
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
if(n % k){
puts("NO");
continue;
}
dfs(1, 0);
if(g == n / k) puts("YES");
else puts("NO");
}
return 0;
}
上面的代码在这个例子下会出错,而实际上wa了一个点...
1
3 1
1 2
1 3
输出NO,而正确答案是YES
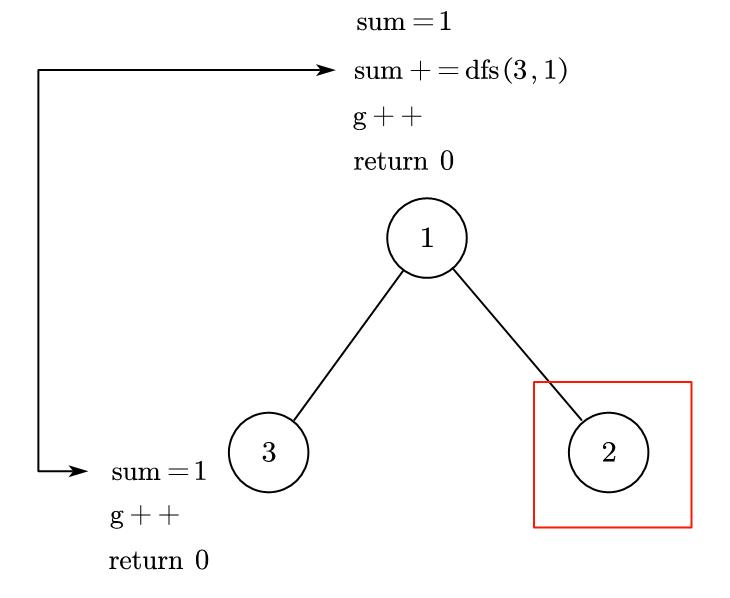
从1开始遍历,先到3,在3处计算得到子树大小为1,满足条件,g++并返回0,回到1所在层,sum+0=sum=1, 发现sum=1,令g++,并返回0,这样的话,最终g=2,因为结点2没有被遍历到。
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int N = 100010;
int h[N], e[N << 1], ne[N << 1], idx;
int T;
int n, k, g;
int cnt[N];
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int dfs(int u, int v){ // 因为按照无向图存储,所以需要存储u是从哪走过来的,避免无限递归
int sum = 1;
for(int i = h[u]; i != -1; i = ne[i]){
int j = e[i];
if(j != v) sum += dfs(j, u);
}
if(sum == k){
g ++;
return 0;
}
return sum;
}
int main(){
cin >> T;
while(T --){
memset(h, -1, sizeof h);
idx = 0;
g = 0;
cin >> n >> k;
for(int i = 0; i < n - 1; i ++){
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
if(n % k){
puts("NO");
continue;
}
dfs(1, 0);
if(g == n / k) puts("YES");
else puts("NO");
}
return 0;
}
复杂度(O(NT))