ABC222

C

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

const int N = 120, M = 110;

int n, m;

struct node{
    int id, val;
    string s;
    
    bool operator<(const node &n){
        if(val != n.val) return val < n.val;  
        return id > n.id;
    }
}stu[N];

int check(char a, char b){
    if(a == b) return 0;
    if(a == 'G'){
        if(b == 'C') return 1;
        if(b == 'P') return -1;
    }
    if(a == 'C'){
        if(b == 'G') return -1;
        if(b == 'P') return 1;
    }
    if(a == 'P'){
        if(b == 'G') return 1;
        if(b == 'C') return -1;
    }
}

void merge(vector<node> &a, vector<node> &b){
    int j = 0, k = 0, u = 0;
    while(j < a.size() && k < b.size()){
        if(a[j] < b[k]) stu[++ u] = a[j ++];
        else stu[++ u] = b[k ++];
    }
    while(j < a.size()) stu[++ u] = a[j ++];
    while(k < b.size()) stu[++ u] = b[k ++];
}

void match(int i){
    vector<node> a, b;
    for(int j = 1; j <= n; j += 2){
        char p = stu[j].s[i], q = stu[j + 1].s[i];
        int st = check(p, q);
        if(st == 0){
            a.push_back(stu[j]);
            a.push_back(stu[j + 1]);
        }else if(st == -1){
            stu[j + 1].val ++;
            a.push_back(stu[j]);
            b.push_back(stu[j + 1]);
        }else{
            stu[j].val ++;
            a.push_back(stu[j + 1]);
            b.push_back(stu[j]);
        }
    }
    merge(a, b);
}

int main(){
    cin >> n >> m;
    n *= 2;
    for(int i = 1; i <= n; i ++){
        stu[i].id = i;
        cin >> stu[i].s;
    }
    
    match(0);
    sort(stu + 1, stu + n + 1);
    
    for(int i = 1; i < m; i ++) match(i);
    
    for(int i = n; i >= 1; i --) cout << stu[i].id << endl;
    
    return 0;
}

D

题意：给定长为n的不降数组a，b，求满足(a_i le c_i le b_i)的不降序列c的个数取模998244353后的值

状态：(f(i, j))表示c的第i个位置放<=j的值且满足升序的所有放法，就是把dp的和前缀和结合了一下

状态转移：

[egin{equation} f(i, j) = egin{cases} f(i - 1, j) + f(i, j - 1), & a_i le j le b_i and j > 0; \ f(i, j - 1), & b_i < j < N; \ f(i - 1, j), & j =0; end{cases} end{equation} ]

初始条件: 其中N时ai, bi能取到的最大值

for(int i = a[0]; i < N; i ++) 
	if(i) f[0][i] = f[0][i - 1] + (i <= b[0]);
    else f[0][i] = 1;

答案：f(n - 1, N - 1)

#include<iostream>
using namespace std;

const int N = 3001, mod = 998244353;

#define int long long

int f[N][N];
int a[N], b[N];
int n;

signed main(){
    cin >> n;
    for(int i = 0; i < n; i ++) cin >> a[i];
    for(int i = 0; i < n; i ++) cin >> b[i];
    
    for(int i = a[0]; i < N; i ++) 
        if(i) f[0][i] = f[0][i - 1] + (i <= b[0]);
        else f[0][i] = 1;
        
    for(int i = 1; i < n; i ++)
        for(int j = a[i]; j < N; j ++){
            if(j) f[i][j] = f[i][j - 1];
            if(j <= b[i])
                f[i][j] = (f[i][j] + f[i - 1][j]) % mod;
        }
        
    cout << f[n - 1][N - 1] << endl;
    
    return 0;
}

E

题意：给你一个树（无环图），共有n个顶点，n - 1条边，给你一个长为m的序列M，和一个整数K(带符号)，可以把每一条边涂成红色或者蓝色，按照序列M中的点在树上走完以后，要求经过蓝色边的次数B和红色边的次数R满足R-B=K，求涂色方案的种数

方法：dfs+dp，按照序列M中的顶点走完以后，每条边的经过的次数是固定的为(C_1, C_2,...,C_{n-1})，那么就可以从C1~Cn中选择一些作为蓝色边的次数，剩下的作为红色边的次数，设(C_1+...+C_{n-1}=s)，设选出来作为红色边的次数的和为t，那么有(t - s + t = k)，那么就是要求在C1~Cn中选择一些数字，是他们的和为(k + s) / 2的所有选法

#include<iostream>
#include<vector>
#include<cstring>

using namespace std;

const int N = 1010, mod = 998244353;

#define int long long

vector<int> s;
int g[N][N], idx;
int n, m, k;
int cnt[N], st[N];
int f[100010];

int dfs(int a, int b){
    if(a == b) return 1;
    st[a] = 1;
    for(int i = 1; i <= n; i ++){
        if(g[a][i] && st[i] == 0){
            cnt[g[a][i]] ++;
            if(dfs(i, b)) return 1;
            st[i] = 0;
            cnt[g[a][i]] --;
        }
    }
    
    return 0;
}

signed main(){
    cin >> n >> m >> k;
    for(int i = 0; i < m; i ++){
        int t;
        cin >> t;
        s.push_back(t);
    }
    
    for(int i = 0; i < n - 1; i ++){
        int a, b;
        cin >> a >> b;
        g[a][b] = g[b][a] = ++ idx;
    }
    
    for(int i = 0; i < (int) s.size() - 1; i ++){
        memset(st, 0, sizeof st);
        dfs(s[i], s[i + 1]);
    }
    
    int sum = 0;
    for(int i = 1; i < n; i ++) sum += cnt[i];
    
    if(sum - k < 0 || (sum - k) % 2){
        puts("0");
        return 0;
    }
    
    sum = (sum - k) / 2;
    
    f[0] = 1;
    
    for(int i = 1; i < n; i ++)
        for(int j = sum; j >= cnt[i]; j --)
            f[j] = (f[j] + f[j - cnt[i]]) % mod;
        
    
    cout << f[sum] << endl;
    
    return 0;

}

F

题意：n个结点的带权(>0)无环图，每一个顶点有一个费用值(>0)，求出每一个结点到其他所有结点能够获得的最大的E值（结点i到结点j的E值就是从i到j的最短路径长度 + j的费用值）

看到题目里面的每一个结点到其他所有结点，就想到floyd，结果跑三重循环T了一半

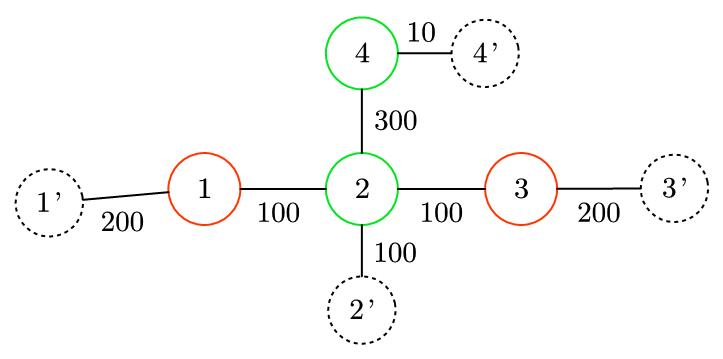
正确做法之一是用树的直径来做，又因为每一个顶点都包含一个费用值d，设原图为G，可以构造图G'如下（这个图不需要实际建出来），给每一个点延伸一个顶点，并让边权为d，然后去求G‘的直径，注意，这里求的直径不是1’，3', 而是用G对照着G', 求G'的直径，所以结果是1，3（因为到达1'只有经过1, 且1到1'只有一条路，所以求到1，3相当于求到了G'的直径），图中绿色的为G的直径，而红色为在G上求出的G'的直径，所以对于G上一个点u，在G上求出的G'的直径端点为x, y，他能达到的最大E值为max(dist(u, x) + d[x], dist(u, y) + d[y])

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>

using namespace std;

const int N = 200010;

#define int long long
#define PII pair<int, int>

struct node{
    int dist, id;
    bool operator > (const node &n) const {
        return dist > n.dist;
    }
};

priority_queue<node, vector<node>, greater<node>> q;

vector<PII> g[N];
int dist[N], distx[N], disty[N], st[N];
int n;
int d[N];

// 给定图是无环图 = 树，一个点到其他点的路径唯一且最短

void dijkstra(int x){
    for(int i = 1; i <= n; i ++) dist[i] = 1e18;
    memset(st, 0, sizeof st);
    
    dist[x] = 0;
    q.push({0, x});
    
    while(q.size()){
        int k = q.top().id;
        q.pop();
        if(st[k]) continue;
        st[k] = 1;
        for(int i = 0; i < g[k].size(); i ++){
            int j = g[k][i].first, w = g[k][i].second;
            if(dist[j] > dist[k] + w){
                dist[j] = dist[k] + w;
                q.push({dist[j], j});
            }
        }
    }
}

signed main(){
    cin >> n;
    for(int i = 0; i < n - 1; i ++){
        int a, b, c;
        cin >> a >> b >> c;
        g[a].push_back({b, c});
        g[b].push_back({a, c});
    }
    
    for(int i = 1; i <= n; i ++) cin >> d[i];
    
    dijkstra(1);
    
    int x, maxv = -1;
    for(int i = 1; i <= n; i ++)
        if(i != 1 && maxv < dist[i] + d[i]){
            maxv = dist[i] + d[i];
            x = i;
        }
      
    dijkstra(x);
    
    int y;
    maxv = -1;
    for(int i = 1; i <= n; i ++)
        if(i != x && maxv < dist[i] + d[i]){
            maxv = dist[i] + d[i];
            y = i;
        }
        
    
    dijkstra(x);
    memcpy(distx, dist, sizeof dist);
    
    dijkstra(y);
    memcpy(disty, dist, sizeof dist);
    
    for(int i = 1; i <= n; i ++){
        int res = -1;
        if(i == x) cout << disty[i] + d[y] << endl;
        else if(i == y) cout << distx[i] + d[x] << endl;
        else cout << max(distx[i] + d[x], disty[i] + d[y]) << endl;
    }
        
    return 0;
}