数据结构复习---排序（1）

选择类排序算法

1、选择排序算法

思想：首先找到数组中最小的那个元素，其次将它和数组中的第一个元素交换（如果第一个元素是最小的，那么和它自己进行交换）。再次，再剩下的元素中找到最小的元素，将它与数组中的第二个元素进行位置交换。如此往复，直到整个数组排序。这就叫选择排序。

时间复杂度 o（n*n）
模板：

public class Example {
    //选择排序算法
    public static void selectSort(Comparable [] a){

    }

    //对元素进行比较
    private static boolean less(Comparable v,Comparable w){
        return v.compareTo(w)<0;
    }
    //将元素交换位置
    private static void exch(Comparable [] a, int i,int j){
        Comparable t=a[i];
        a[i]=a[j];
        a[j]=t;
    }
    public static void show(Comparable [] a){
        //在单行中打印数组
        for(int i=0;i<a.length;i++){
            System.out.print(a[i]+" ");
        }
        System.out.println();
    }
    public static boolean isSorted(Comparable[] a){
        //测试元素是否有序
        for(int i=1;i<a.length;i++)
            if(less(a[i],a[i-1])) return false;
        return true;
    }

    public static void main(String[] args) {
             Comparable[] sort={1,2,4,3,0};
             selectSort(sort);
             show(sort);
    }
}

//选择排序算法
    public static void selectSort(Comparable [] a){
        //将a[] 按照升序排列
        int N=a.length;
        for(int i=0;i<N;i++){
            int min=i;
            for(int j=i+1;j<N;j++){
                if(less(a[j],a[min])) min=j;
            }
            exch(a,i,min);
        }
    }

测试结果

2、堆排序算法

　　堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。
　　堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：
　　

该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：
大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

堆排序的思想：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。
时间复杂度： o(nlogn)

图解博客：https://www.cnblogs.com/chengxiao/p/6129630.html

 //建立大顶堆
    public static void heapSort(Comparable []a){
        //1.建立大顶堆
        for (int i = a.length/2-1; i >=0 ; i--) {
            adjustHeap(a,i,a.length);
        }
        //2.跳整堆结构  交换顶元素与末尾元素
        for(int j=a.length-1;j>0;j--){
            //将对顶元素与末尾元素进行交换
            exch(a,0,j);
            //重新对堆进行排序
            adjustHeap(a,0,j);
        }
    }

//调整大顶堆（只是调整过程，建立在大顶堆已经构建的基础之上）
    private static void adjustHeap(Comparable[] a, int i, int length) {
        Comparable temp = a[i];//先取出当前元素i
        for(int k=i*2+1;k<length;k=k*2+1){//从i结点的左子结点开始，也就是2i+1处开始
            if(k+1<length && less(a[k],a[k+1])){//如果左子结点小于右子结点，k指向右子结点
                k++;
            }
            if(less(temp,a[k])){//如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）
                a[i] = a[k];
                i = k;
            }else{
                break;
            }
        }
        a[i] = temp;//将temp值放到最终的位置
    }

插入类排序算法

1、直接插入排序算法

用整理牌的思想来解释，将每一张牌插入到已经有序的牌中的适当的位置。一直到牌排序完。

时间复杂度 o（n*n）

 //插入排序算法
    public static void insertSort(Comparable [] a){
        //将a[]按照升序排列
       int N =a.length;
        for (int i = 0; i <N ; i++) {
            //将a[i]插入到。。。
            for(int j=i;j>0;j--){
                //如果a[j]比a[j-1]要小的话
                if(less(a[j],a[j-1]))
                    exch(a,j,j-1);
            }
        }
    }

2、希尔排序

（1）希尔排序（shell sort）这个排序方法又称为缩小增量排序，是1959年D·L·Shell提出来的。该方法的基本思想是：设待排序元素序列有n个元素，首先取一个整数increment（小于n）作为间隔将全部元素分为increment个子序列，所有距离为increment的元素放在同一个子序列中，在每一个子序列中分别实行直接插入排序。然后缩小间隔increment，重复上述子序列划分和排序工作。直到最后取increment=1，将所有元素放在同一个子序列中排序为止。
（2）由于开始时，increment的取值较大，每个子序列中的元素较少，排序速度较快，到排序后期increment取值逐渐变小，子序列中元素个数逐渐增多，但由于前面工作的基础，大多数元素已经基本有序，所以排序速度仍然很快。
（3）希尔排序举例：
1>下面给出一个数据列：

2>第一趟取increment的方法是：n/3向下取整+1=3（关于increment的取法之后会有介绍）。将整个数据列划分为间隔为3的3个子序列，然后对每一个子序列执行直接插入排序，相当于对整个序列执行了部分排序调整。图解如下：

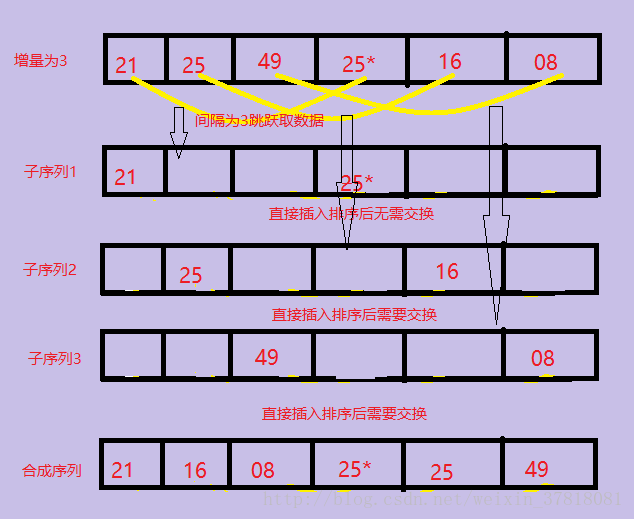
3>第二趟将间隔increment= increment/3向下取整+1=2，将整个元素序列划分为2个间隔为2的子序列，分别进行排序。图解如下：

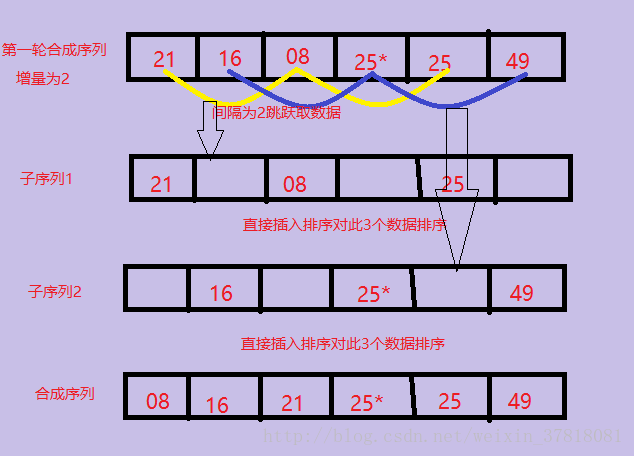
4>第3趟把间隔缩小为increment= increment/3向下取整+1=1，当增量为1的时候，实际上就是把整个数列作为一个子序列进行插入排序，图解如下：

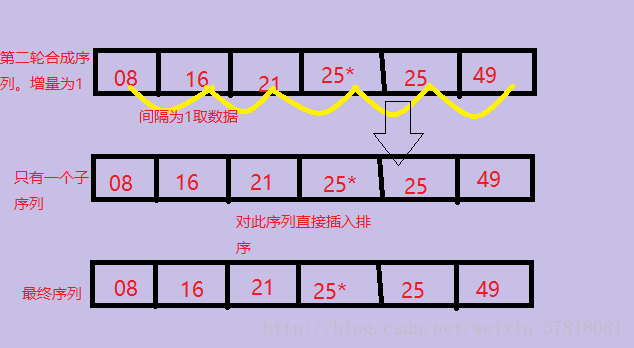
5>直到increment=1时，就是对整个数列做最后一次调整，因为前面的序列调整已经使得整个序列部分有序，所以最后一次调整也变得十分轻松，这也是希尔排序性能优越的体现。
（4）希尔排序算法的代码实现 java

  //希尔排序
    public static void shellSort(Comparable [] a){
        //将a[]按照升序排列
        int N=a.length;
        int h=1;
        while(h<N/3)
            h=3*h+1;
        while(h>=1){
            //将数组变成h有序
            for (int i = h; i <N ; i++) {
                for(int j=i;j>=h;j-=h){
                    if(less(a[j],a[j-h]))
                        exch(a,j,j-h);
                }
            }
            h=h/3;
        }
    }

（5）关于希尔排序increment（增量）的取法。
增量increment的取法有各种方案。最初shell提出取increment=n/2向下取整，increment=increment/2向下取整，直到increment=1。但由于直到最后一步，在奇数位置的元素才会与偶数位置的元素进行比较，这样使用这个序列的效率会很低。后来Knuth提出取increment=n/3向下取整+1.还有人提出都取奇数为好，也有人提出increment互质为好。应用不同的序列会使希尔排序算法的性能有很大的差异。
（6）希尔排序应该注意的问题
从上面图解希尔排序的过程可以看到，相等的排序码25在排序前后的顺序发生了颠倒，所以希尔排序是一种不稳定的排序算法。

时间复杂度 o(n*n)
参考文章：https://blog.csdn.net/weixin_37818081/article/details/79202115
https://www.cnblogs.com/chengxiao/p/6129630.html