介绍
Paxos算法是基于消息传递且具有高度容错特性的一致性算法,是目前公认的解决分布式一致性问题最有效的算法之一,其解决的问题就是在分布式系统中如何就某个值(决议)达成一致。
在常见的分布式系统中,总会发生诸如机器宕机或网络异常(包括消息的延迟、丢失、重复、乱序,还有网络分区)(也就是会发生异常的分布式系统)等情况。Paxos算法需要解决的问题就是如何在一个可能发生上述异常的分布式系统中,快速且正确地在集群内部对某个数据的值达成一致。也可以理解成分布式系统中达成状态的一致性。
Paxos算法运行在允许宕机故障的异步系统中,不要求可靠的消息传递,可容忍消息丢失、延迟、乱序以及重复。它利用大多数 (Majority) 机制保证了2F+1的容错能力,即2F+1个节点的系统最多允许F个节点同时出现故障。
一个或多个提议进程 (Proposer) 可以发起提案 (Proposal),Paxos算法使所有提案中的某一个提案,在所有进程中达成一致。系统中的多数派同时认可该提案,即达成了一致。最多只针对一个确定的提案达成一致。
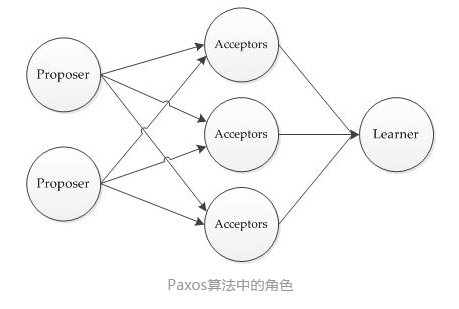
Paxos将系统中的角色分为提议者 (Proposer),决策者 (Acceptor),和最终决策学习者 (Learner):
-
- Proposer: 提出提案 (Proposal)。Proposal信息包括提案编号 (Proposal ID) 和提议的值 (Value)。
- Acceptor:参与决策,回应Proposers的提案。收到Proposal后可以接受提案,若Proposal获得多数Acceptors的接受,则称该Proposal被批准。
- Learner:不参与决策,从Proposers/Acceptors学习最新达成一致的提案(Value)。
在多副本状态机中,每个副本同时具有Proposer、Acceptor、Learner三种角色。
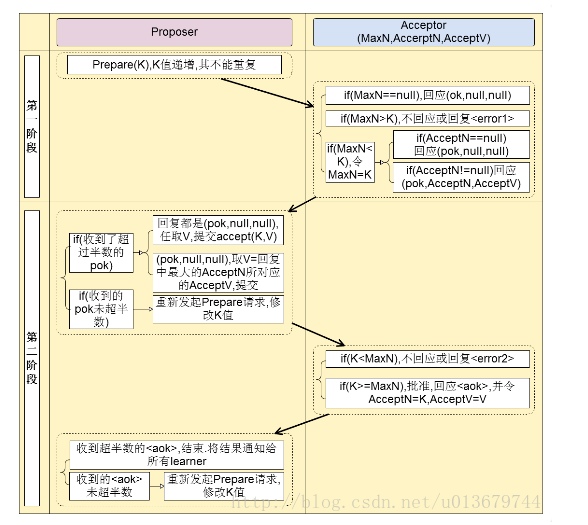
Paxos算法通过一个决议分为两个阶段(Learn阶段之前决议已经形成):
阶段一(prepare阶段):
(a) Proposer选择一个提案编号N,然后向半数以上的Acceptor发送编号为N的Prepare请求。Pareper(N)
(b) 如果一个Acceptor收到一个编号为N的Prepare请求,如果小于它已经响应过的请求,则拒绝,不回应或回复error。若N大于该Acceptor已经响应过的所有Prepare请求的编号(maxN),那么它就会将它已经接受过(已经经过第二阶段accept的提案)的编号最大的提案(如果有的话,如果还没有的accept提案的话返回{pok,null,null})作为响应反馈给Proposer,同时该Acceptor承诺不再接受任何编号小于N的提案。
阶段二(accept阶段):
(a) 如果一个Proposer收到半数以上Acceptor对其发出的编号为N的Prepare请求的响应,那么它就会发送一个针对[N,V]提案的Accept请求给半数以上的Acceptor。注意:V就是收到的响应中编号最大的提案的value(某个acceptor响应的它已经通过的{acceptN,acceptV}),如果响应中不包含任何提案,那么V就由Proposer自己决定。
(b) 如果Acceptor收到一个针对编号为N的提案的Accept请求,只要该Acceptor没有对编号大于N的Prepare请求做出过响应,它就接受该提案。如果N小于Acceptor以及响应的prepare请求,则拒绝,不回应或回复error(当proposer没有收到过半的回应,那么他会重新进入第一阶段,递增提案号,重新提出prepare请求)。
参考:https://blog.csdn.net/u013679744/article/details/79222103
https://zhuanlan.zhihu.com/p/31780743