基本数据结构 -- 二叉查找树的插入、删除、查找和遍历

一、什么是二叉查找树

　　二叉查找树（Binary Search Tree）是一种特殊的二叉树，对于一个二叉查找树，树中的每个结点X，它的左子树中所有关键字的值都小于X的关键字值；而它的右子树中所有关键字的值大于X的关键字值。这意味着，该树的所有元素可以使用一种统一的方式进行排序，因此，二叉查找树又称为二叉排序树。下图即为一个二叉查找树：

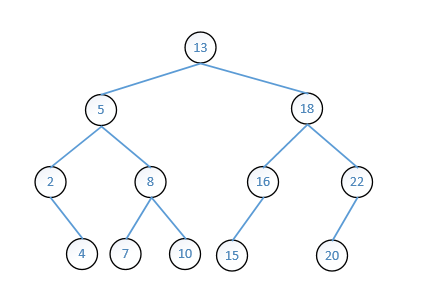
二、如何在 BST 中查找一个结点

　　二叉查找树很适合进行查找操作。以上图中的二叉查找树为例：如果需要在该 BST 中查找值 10，先从根结点开始进行比较，10小于13，根据 BST 的性质，可以知道如果该 BST 中有结点值为10的话，那么该结点必然位于根结点的左子树中；再从结点 5 开始，可知 10 在结点 5 的右子树；再从结点 8 开始，10 在结点 8 的右子树，最终找到元素 10。

　　用算法来描述，在一个 二叉查找树 T（T 为二叉树的根结点）中查找元素 n：

1）若 T 为空，则 n 不在 BST 中；

2）判断 n 与根结点值（T->val）的关系；

3）如果 n 等于 T->val，则找到了元素 n;

4）如果 n 大于 T->val，则去根结点的右子树 (T->right) 继续查找。将 T->right 作为 T，回到第 1 步；

5）如果 n 小于 T->val，则去根结点的左子树 (T->left ) 继续查找。将 T->left 作为 T，回到第1步。

　　算法实现如下：

typedef int ElementType;

typedef struct BinaryTreeNode_ {
    ElementType val;
    struct BinaryTreeNode_ *left;
    struct BinaryTreeNode_ *right;
}BinaryTreeNode;

typedef BinaryTreeNode *BiTreeNode;

// 查找一个结点
BiTreeNode FindNode(BiTreeNode BiTree,ElementType n)
{
    if (BiTree == NULL)        // 如果头结点为空，表明没有找到元素 n
        return NULL;
    if (BiTree->val < n)    // 结点值小于查找元素值，说明元素在结点的右边
        return FindNode(BiTree->right, n);    // 递归，去右子树继续查找
    else if (BiTree->val > n)
        return FindNode(BiTree->left, n);    // 递归，去左子树继续查找
    else
        return BiTree;
} 

 　　该查找算法的时间复杂度为 O(log₂N)。

三、向 BST 中插入一个结点

　　向 BST 中插入一个结点 n 时，若 BST 中已经存在与该结点值相等的结点，则判断结点已存在，不做任何操作；如果 BST 中不存在该结点，则将该结点将作为一个新的叶子结点插入到 BST 中去（新结点总是 BST 的叶子结点），且需要保证插入后的树是一个二叉查找树。

　　可以以类似查找算法的方式来遍历二叉树，从而找到插入的位置：

　　用算法来描述，向一个二叉查找树 T（T 为二叉树的根结点）中插入一个结点，节点元素为 n：

1）若 T 为空，则将新结点插入到 T 所在的位置；

2）若 T 不为空，且 T->val 小于 n，则表明应该把 n 插入到 T 的右子树。将 T->right 作为 T，回到第 1 步；

3）若 T 不为空，且 T->val 大于 n，则表明应该把 n 插入到 T 的左子树。将 T->left 作为 T，回到第 1 步。

4）若 T->val 等于 n，则直接返回 T。

// 插入一个结点
BiTreeNode InsertNode(BiTreeNode BiTree, ElementType n)
{
    if (BiTree == NULL) {    // 树为空，或已到达叶子结点
        // 为新结点分配内存
        BiTreeNode newNode = (BiTreeNode)malloc(sizeof(BinaryTreeNode));
        if (newNode == NULL) {
            perror("malloc failed!
");
            exit(EXIT_FAILURE);
        }
        newNode->val = n;
        newNode->left = NULL;
        newNode->right = NULL;
        BiTree = newNode;
    }
    else if (BiTree->val < n) {    // 插入值大于当前结点的值，则将元素插入到结点的右子树
        BiTree->right = InsertNode(BiTree->right, n);
    }
    else if (BiTree->val > n) {    // 插入值小于当前结点的值，则将元素插入到结点的左子树
        BiTree->left = InsertNode(BiTree->left, n);
    }
    
    return BiTree;
    
}

四、遍历 BST

　　在上一篇博客中已经介绍了二叉树的遍历方法，主要有三种：先序遍历、后序遍历和中序遍历。为了更好的体现二叉查找树的特性，我们使用中序遍历来遍历它：

// 中序遍历 BST
void TraverseTree(BiTreeNode BiTree)
{
    if (BiTree != NULL) {
        TraverseTree(BiTree->left);
        cout << BiTree->val << endl;
        TraverseTree(BiTree->right);
    }

}

五、删除一个结点

　　删除操作比较复杂，分为三种情况：

1）被删除结点为叶子结点：

　　可以直接删除该结点，如图：

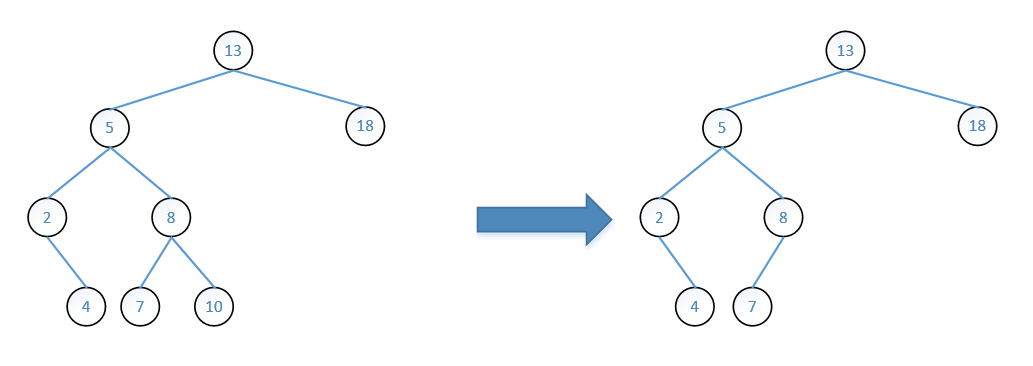
2）被删除结点有一个左孩子或一个右孩子：

　　将孩子结点设为该结点的父结点的孩子后，即可删除该结点：

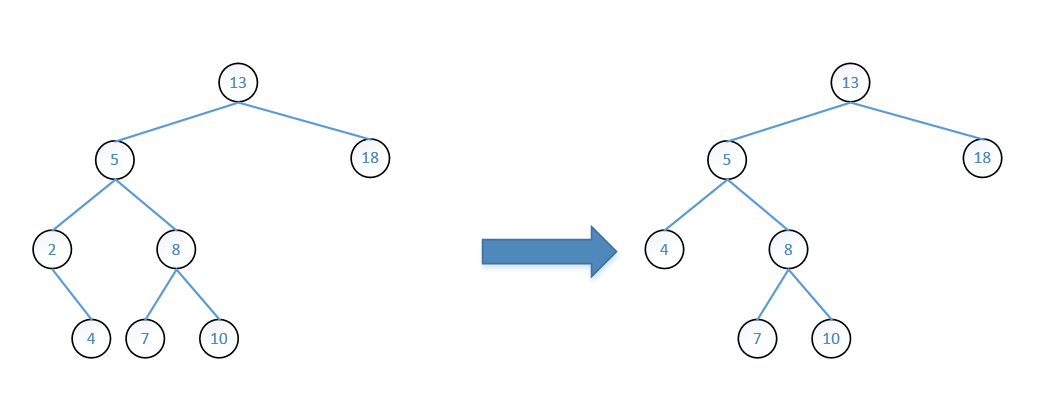
　　如图，结点 2 是结点 5 的左孩子，他有一个右孩子 4。删除结点 2 后，其右孩子 4 替代原来的结点 2 成为结点 5 的左孩子。

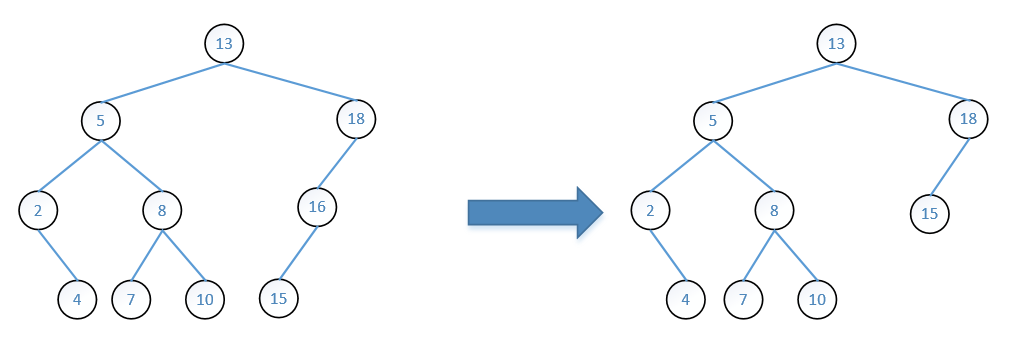
　　如图，结点 16 是结点 18 的左孩子，他有一个左孩子 15。删除结点 16 后，其左孩子 15 替代原来的结点 16 成为结点 18 的左孩子。

3）被删除结点有两个孩子结点：

　　这种情况比较复杂，一般的删除策略是：用被删除结点的右子树中的最小结点替代被删除结点，并递归地删除这个最小数据结点：

// 删除一个结点
BiTreeNode DeleteNode(BiTreeNode BiTree, ElementType n)
{
    BiTreeNode tmpNode = (BiTreeNode)malloc(sizeof(BinaryTreeNode));
    if (tmpNode == NULL) {
        perror("malloc failed!
");
        exit(EXIT_FAILURE);
    }

    // 先找到要删除的结点在二叉树中的位置
    if (BiTree == NULL) {    // 没有找到元素
        perror("can`t find element
");
        return NULL;
    }
        
    if (BiTree->val < n) {        // 元素值大于结点元素值，则去结点右子树寻找
        BiTree->right = DeleteNode(BiTree->right, n);
        return BiTree;
    }
    else if (BiTree->val > n) {    // 元素值小于结点元素值，则去结点左子树寻找
        BiTree->left = DeleteNode(BiTree->left, n);
        return BiTree;
    }
    // 找到结点
    else {
        tmpNode = BiTree;
        if (BiTree->right == NULL) {        // 没有右子树，则直接返回左子树
            BiTree = BiTree->left;
            return BiTree;
        }
        else if (BiTree->left == NULL) {    // 没有左子树，则直接返回右子树
            BiTree = BiTree->right;
            return BiTree;
        }
        // 有两个孩子结点
        tmpNode = FindMin(BiTree->right);    // 寻找右子树最小结点
        tmpNode->right = DeleteMin(BiTree->right);    // 删除右子树的最小结点
        tmpNode->left = BiTree->left;        // 左子树保持不变
        return tmpNode;
    }
}

// 查找最左叶子结点（最小的结点）
BiTreeNode FindMin(BiTreeNode BiTree)
{
    if (BiTree == NULL)
        return NULL;
    if (BiTree->left == NULL)    // 结点没有左子树，即为最左叶子结点
        return BiTree;
    else        // 有左子树，则继续在左子树中查找
        return FindMin(BiTree->left);
}

// 删除最小结点
BiTreeNode DeleteMin(BiTreeNode BiTree)
{
    if (BiTree->left == NULL)
        return BiTree->right;
    else {
        BiTree->left = DeleteMin(BiTree->left);
        return BiTree;
    }

}

参考资料：

《数据结构与算法分析 C 语言描述》