完全二叉树(堆)和满二叉树的结构:

完全二叉树的判断:
二叉树的层次遍历(BFS)
堆的存储
使用数组存储,i结点的父结点下标就为(i–1)/2。它的左右子结点下标分别为2*i+1和2*i+2

堆的初始化:
直接使用数组存储,然后堆化数组即可:
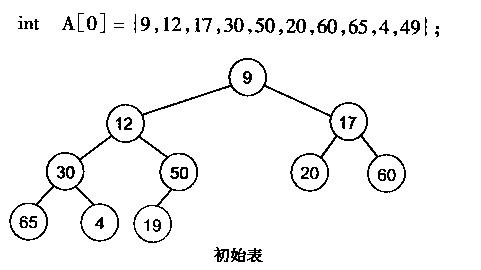
从下至上,从右到左,逐步堆化。

堆的增删改查:
增:插入堆尾,从下往上冒泡。
删:删除堆顶元素时,堆顶元素和堆尾元素交换(同时删除堆顶元素),从上往下冒泡即可。
改:增+删
查:O(logN)
删除任意元素:
《算法导论》Chapter6的习题6.5-8
将a[i]与堆尾a[n-1]交换,然后分情况讨论:
①a[i]=a[n-1]无须操作
②a[i]>a[n-1]执行删除元素操作
③a[i]<a[n-1]重新维护a[i]所在的子堆
堆的排序:
每次执行一次删除堆顶的操作(将堆顶和堆尾交换),共N次,每次删除需要执行一次从上往下冒泡,复杂度为O(LogN),总时间复杂度为O(NLogN),最小堆排序之后为降序数组。