数据结构——二叉查找树、AVL树

二叉查找树：由于二叉查找树建树的过程即为插入的过程，所以其中序遍历一定为升序排列！

插入：直接插入，插入后一定为根节点

查找：直接查找

删除：叶子节点直接删除，有一个孩子的节点删除后将孩子节点接入到父节点即可，有两个孩子的节点，将左儿子最右边节点（或右儿子最左边节点）替换到根节点即可。

AVL树（二叉平衡查找树）

定义：节点的平衡度(左子树的高度 - 右子树的高度)只能为-1、0、1的二叉查找树。

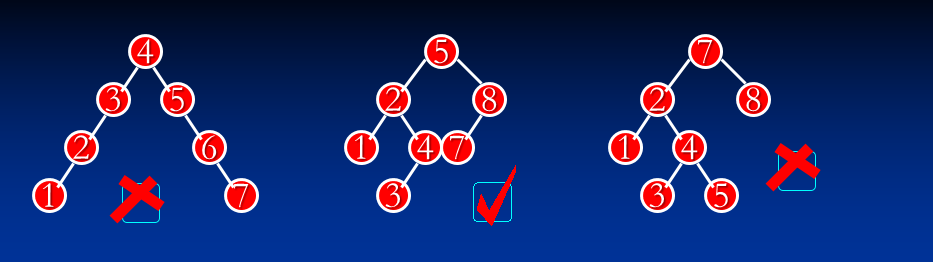
创建：需要一个变量记录每个节点的平衡度

查找：直接查找

插入：LL、LR、RL、RR过程

删除：分情况讨论

AVL树的Java实现：

package com.tonyluis;

/**
 * AVL树
 * 
 * @author TonyLuis 2016.07.27
 * @param <T>
 */
public class AVLTree<T extends Comparable<T>> {
	private AVLNode<T> root;

	@SuppressWarnings("hiding")
	class AVLNode<T> {
		T val;
		AVLNode<T> left;
		AVLNode<T> right;
		int height;

		AVLNode(T val, AVLNode<T> left, AVLNode<T> right) {
			this.val = val;
			this.left = left;
			this.right = right;
			this.height = 0;
		}
	}

	public void insert(T num) {
		root = insert(num, root);
	}

	public void remove(T num) {
		remove(num, root);
	}

	public boolean find(T num) {
		AVLNode<T> t = this.root;
		while (t != null && num.compareTo(t.val) != 0)
			t = num.compareTo(t.val) > 0 ? t.right : t.left;
		if (t == null)
			return false;
		else
			return true;
	}

	private int height(AVLNode<T> node) {
		return node == null ? -1 : node.height;
	}

	private AVLNode<T> insert(T num, AVLNode<T> root) {
		// root==null 找到了插入的位置
		if (root == null)
			return new AVLNode<T>(num, null, null);

		int compareResult = num.compareTo(root.val);
		if (compareResult < 0) {// 插入左子树
			root.left = insert(num, root.left);
			if (height(root.left) - height(root.right) == 2) {
				if (num.compareTo(root.left.val) < 0)
					root = LL(root);
				else
					root = LR(root);
			}
		} else if (compareResult > 0) {
			root.right = insert(num, root.right);
			if (height(root.right) - height(root.left) == 2) {
				if (num.compareTo(root.right.val) < 0)
					root = RL(root);
				else
					root = RR(root);
			}
		}
		root.height = Math.max(height(root.left), height(root.right)) + 1;
		return root;
	}

	public boolean remove(T num, AVLNode<T> root) {
		boolean isStop = false;
		boolean isLeftSubTree;
		if (root == null)
			return true;
		int compareResult = num.compareTo(root.val);
		if (compareResult < 0) {
			isStop = remove(num, root.left);
			isLeftSubTree = true;
		} else if (compareResult > 0) {
			isStop = remove(num, root.right);
			isLeftSubTree = false;
		} else if (root.left == null || root.right == null) {
			root = root.left == null ? root.right : root.left;
			return false;
		} else {// 找到且有两个子树，将其和右子树最左边节点交换，然后在右子树执行删除操作
			AVLNode<T> tmp = root.right;
			while (tmp.left != null)
				tmp = tmp.left;
			root.val = tmp.val;
			isStop = remove(root.val, root.right);
			isLeftSubTree = false;
		}
		if (isStop)
			return true;
		int bf;// 删除前的root的平衡因子
		if (isLeftSubTree) {
			bf = height(root.left) - height(root.right) + 1;
			if (bf == 0)
				return true;
			else if (bf == 1)
				return false;
			else if (bf == -1) {
				int bfr = height(root.right.left) - height(root.right.left);
				switch (bfr) {
				case 0:
					RR(root);
					return true;
				case -1:
					RR(root);
					return false;
				default:
					RL(root);
					return false;
				}
			}
		} else {
			bf = height(root.left) - height(root.right) - 1;
			if (bf == 0)
				return true;
			else if (bf == -1)
				return false;
			else if (bf == 1) {
				int bfr = height(root.right.left) - height(root.right.left);
				switch (bfr) {
				case 0:
					LL(root);
					return true;
				case 1:
					LL(root);
					return false;
				default:
					LR(root);
					return false;
				}
			}
		}
		return false;
	}

	private AVLNode<T> LL(AVLNode<T> node) {
		AVLNode<T> nodeLeft = node.left;
		node.left = nodeLeft.right;
		nodeLeft.right = node;
		node.height = Math.max(height(node.left), height(node.right)) + 1;
		nodeLeft.height = Math.max(height(nodeLeft.left), node.height) + 1;
		return nodeLeft;
	}

	private AVLNode<T> RR(AVLNode<T> node) {
		AVLNode<T> nodeRight = node.right;
		node.right = nodeRight.left;
		nodeRight.left = node;
		node.height = Math.max(height(node.left), height(node.right)) + 1;
		nodeRight.height = Math.max(height(nodeRight.right), node.height) + 1;
		return nodeRight;
	}

	private AVLNode<T> LR(AVLNode<T> node) {
		node.left = RR(node.left);
		return LL(node);
	}

	private AVLNode<T> RL(AVLNode<T> node) {
		node.right = LL(node.right);
		return RR(node);
	}

}