- 递归二分查找
- 冒泡排序
- 选择排序
- 插入排序
- 归并排序
- 快速排序
1、递归二分查找
思想:
使用二分查找的前提条件是数组元素必须已经排好序。
- 二分查找法首先将关键字与数组的中间元素进行比较,考虑下面三种情形:
- 如果关键字比中间元素小,那么只需在前一半数组元素中进行递归查找;
- 如果关键字与中间元素相等,则匹配成功,查找结束。
代码:
public static int binarySearch(int[] list, int key){ return binarySearch(list, key, 0, list.length - 1); } public static int binarySearch(int[] list, int key , int low, int high){ //没有查找到 if(low > high) return - low - 1; int mid = (low + high) / 2; if(key < list[mid]){ return binarySearch(list, key, low, mid - 1); }else if(key == list[mid]){ return mid; }else{ return binarySearch(list, key, mid + 1, high); } }
------------------------------------------------- 排序算法 ----------------------------------------------
各排序算法的时间复杂度、空间复杂度、稳定性:
(排序算法的稳定性:排序前后相等元素的相对位置不变,则称排序算法是稳定的;否则排序算法是不稳定的)
排序算法 平均时间复杂度 最坏时间复杂度 空间复杂度 稳定性 冒泡排序 O(n^2) O(n^2) O(1) 稳定 选择排序 O(n^2) O(n^2) O(1) 不稳定 直接插入排序 O(n^2) O(n^2) O(1) 稳定 归并排序 O(nlogn) O(nlogn) O(n)
稳定 快速排序 O(nlogn) O(n^2) O(logn) 不稳定 堆排序 O(nlogn) O(nlogn) O(1) 不稳定 冒泡排序:
冒泡排序算法需要多次遍历数组(N-1次),在每次遍历中,比较连续相邻的元素。如果一对元素是降序,则互换它们的值;否则保持不变。这样每一次遍历较大的值都沉到了后面:第一次遍历区间为0~N-1,第一次遍历后,最后一个元素成为数组中最大的数;第二次遍历区间为0~N-2,第二次遍历后,倒数第二个元素成为第二大的数……
- 稳定性:稳定。冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。如果两个元素相等,不会把他们俩交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
- 时间复杂度:O(n^2)。需要两个for循环,每次只关注一个元素,平均时间复杂度为O(n^2),最坏的也是O(n^2)。
- 空间复杂度:O(1)。需要一个临时变量来交换元素位置,所以空间复杂度O(1)。
选择排序:
选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择最小的,依次类推,直到第n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。
- 稳定性:不稳定。在一趟选择中,如果当前元素比一个元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。比如序列5 8 5 2 9, 我们知道第一遍选择第1个元素5会和2交换,那么原序列中2个5的相对前后顺序就被破坏了,所以选择排序不是一个稳定的排序算法。
- 时间复杂度:O(n^2)。需要两个for循环,平均时间复杂度为O(n^2),最坏的也是O(n^2)。
- 空间复杂度:O(1)。需要一个临时变量来交换元素位置,所以空间复杂度O(1)。
插入排序:
插入排序是重复的将新的元素插入一个排好序的子线性表中,直到整个线性表排好序。插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。当然,刚开始这个有序的小序列只有1个元素,就是第一个元素。比较是从有序序列的末尾开始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置......
- 稳定性:稳定。如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变。
- 时间复杂度:O(n^2)。需要两个for循环,平均时间复杂度为O(n^2)。最坏时间O(n^2),最好时间O(n),就是不用交换。
- 空间复杂度:O(1)。需要一个临时变量来交换元素位置,所以空间复杂度O(1)。
归并排序:
归并排序是使用分而治之法对数组排序。将数组分为两半,对每部分递归地应用归并排序。在两部分都排好序后,对它们进行归并。先什么都不管,把数组分为两个子数组,一直递归把数组划分为两个子数组,直到数组里只有一个元素,这时候才开始排序,让两个数组间排好序,依次按照递归的返回来把两个数组进行排好序,到最后就可以把整个数组排好序。
做法:分成两个函数:1)划分数组;2)归并两个有序数组。划分时创建两个临时数组,将数组前半部分与后半部分复制到临时数组中。归并时将它们先排序再归并到原始数组中。
- 稳定性:稳定。在短序列只有1个或2个元素时,1个元素不会交换,2个元素如果大小相等也不交换,这不会破坏稳定性。那么,在短的有序序列合并的过程中,稳定是否受到破坏?没有,合并过程中我们可以保证如果两个当前元素相等时,我们把处在前面的序列的元素保存在结果序列的前面,这样就保证了稳定性。
- 时间复杂度:O(nlogn)。归并排序将数组划分为两个子数组,使用同样的算法对子数组进行递归排序,然后将子数组进行归并,因此T(n)=T(n/2)+T(n/2)+归并用时。第一项是对数组的前半部分排序所需的时间,第二项是对数组的后半部分排序所需的时间。要归并两个数组,最多需要n-1次比较来比较两个子数组中的元素,以及n次移动将元素移到临时数组中,因此归并总时间为2n-1。因此T(n)=T(n/2)+T(n/2)+2n-1=O(nlogn)。
- 空间复杂度:O(n)。归并排序每次递归需要用到一个辅助表,长度与待排序的表相等,虽然递归次数是O(log2n),但每次递归都会释放掉所占的辅助空间,所以下次递归的栈空间和辅助空间与这部分释放的空间就不相关了,这样每一个时刻需要O(n)个空间即可,因而空间复杂度还是O(n)。
快速排序:
在数组中选择一个基准元素(pivot),将数组分为两部分,使得第一部分中的所有元素都小于等于pivot,第二部分的所有元素都大于pivot。对第一部分递归的应用快速排序算法,然后对第二部分递归的应用快速排序算法。
- 稳定性:不稳定。快速排序有两个方向,右边的j下标一直往左走,当a[j] > pivot,左边的i下标一直往右走,当a[i] <= pivot。如果i和j都走不动了,i <= j, 交换a[i]和a[j],重复上面的过程,直到i>j,交换a[j]和pivot,完成一趟快速排序。在基准元素pivot和a[j]交换的时候,很有可能把前面的元素的稳定性打乱,比如序列为 5 3 3 4 3 8 9 10 11, 现在基准元素5和3交换就会把元素3的稳定性打乱,所以快速排序是一个不稳定的排序算法,不稳定发生在基准元素和a[j]交换的时刻。
- 时间复杂度:O(nlogn)。
- 最差情况下,划分由n个元素构成的数组需要进行n次比较和n次移动,划分所需时间为O(n),在最差情况下,基准元素每次会将数组划分为一个大的子数组和另外一个空数组,这个大的子数组的大小是在划分前的子数组的大小上减1,该算法需要()+()+...+2+1=O(n^2)时间。
- 最佳情况下,基准元素每次将数组划分为规模大致相等的两部分,则T(n)=T(n/2)+T(n/2)+划分用时,其中前两项表示在两个子数组上进行递归的快速排序用时,划分用时为O(n),则T(n)=T(n/2)+T(n/2)+n=O(nlogn)。
- 空间复杂度:O(logn)。快速排序每次递归都会返回一个中间值的位置。最优的情况下空间复杂度为O(logn) ,即每一次都平分数组的情况;最差的情况下空间复杂度为O(n) ,即退化为冒泡排序的情况。
堆排序:
堆排序使用一个二叉堆,它首先将所有的元素添加到一个堆上,然后不断移除最大的元素以获得一个排好序的线性表。
该二叉堆是一个完全二叉树,该二叉树具有如下属性:首先它是一个完全二叉树(二叉树的每层都是满的,或者最后一层没填满并且最后一层的叶子都是靠最左放置的),其次每个结点大于或等于它的任意一个孩子。
- 稳定性:不稳定。
- 时间复杂度:O(nlogn)。
设h表示n个元素的堆的高度。由于堆是一颗完全二叉树,所以第一层有1(2^0)个结点,第二层有2(2^1)个结点,....,第h层有2^(h-1)个结点,最后第h+1层最少有1个最多有2^h个结点。因此1+2+...+2^(h-1)<n<=1+2+...+2^(h-1)+2^h,即2^h < n+1 <= 2^(h+1),所以h < log(n+1) <= h+1。所以堆的高度为O(logn)。
- 由于add方法会最追踪从叶子结点到根节点的路径,因此向堆中添加一个新元素最多需要h步,所以建立一个包含n个元素的数组的初始堆需要O(nlogn)时间。
- 因为remove方法要追踪从根节点到叶子结点的路径,因此从堆中删除根节点后重建堆最多需要n步。由于要调用n次remove方法,所以由堆产生一个有序数组需要时间为O(nlogn)。
- 空间复杂度:O(1)。只是需要一个临时变量来交换元素位置,所以空间复杂度O(1)。
1、冒泡排序
动画演示:http://liveexample.pearsoncmg.com/dsanimation/BubbleSortNeweBook.html
思路:
依次比较相邻的两个数,将小数放在前面,大数放在后面。
即在第一趟:首先比较第1个和第2个数,将小数放前,大数放后。然后比较第2个数和第3个数,将小数放前,大数放后,如此继续……直至比较最后两个数,将小数放前,大数放后。重复第一趟步骤,直至全部排序完成。
第一趟比较完成后,最后一个数一定是数组中最大的一个数,所以第二趟比较的时候最后一个数不参与比较;
第二趟比较完成后,倒数第二个数也一定是数组中第二大的数,所以第三趟比较的时候最后两个数不参与比较;
依次类推,每一趟比较次数-1;
……
稳定性:稳定
时间复杂度:O(n^2)
空间复杂度:O(1)
代码:
public static void bubbleSort(int[] array) { // 优化:如果在某次遍历中没有发生交换,那么就不用再进行下一次遍历了,因为所有元素已经排好序了 boolean needNextPass = true; //需要array.length-1次遍历 for(int k = 1; k < array.length && needNextPass; k++){ needNextPass = false; //假设不需要进行下次遍历 //第k次遍历处理前array.length-k个数 for(int i = 0; i < array.length - k; i++){ //依次比较相邻两个元素 if(array[i] > array[i + 1]){ //交换 int temp = array[i]; array[i] = array[i + 1]; array[i + 1] = temp; needNextPass = true; //需要进行下次遍历 } } } }
2、选择排序
动画演示:http://liveexample.pearsoncmg.com/dsanimation/SelectionSortNeweBook.html
思路:
找数组中最小的数,并将其和第一个数交换;
然后从剩下的数中找最小的数,和第二个交换;
……一直进行下去,直到仅剩一个数 (是一个递归的过程)
稳定性:不稳定
时间复杂度:O(n^2)
空间复杂度:O(1)
代码:
//主程序初始时候执行 selectionSort(array,0, array.length - 1) public static void selectionSort(double[] array, int low, int high){ if(low < high){ int indexOfMin = low; //最小数下标 double min = array[low]; //最小数 //找到最小的数min和最小数下标indexOfMin for(int i = low + 1; i <= high; i++){ if(array[i] < min){ min = array[i]; indexOfMin = i; } } //交换第low个元素与min array[indexOfMin] = array[low]; array[low] = min; //递归 selectionSort(array, low + 1, high); } }
3、插入排序
动画演示:http://liveexample.pearsoncmg.com/dsanimation/InsertionSortNeweBook.html
思路:
重复的将新的元素插入一个排好序的子线性表中,直到整个线性表排好序。
[0,1,4,6,3]
我们要做的从a[1]开始,至于为什么不是a[0]。a[0]之前没有与a[0]进行比较的元素。我们插入a[1],这个时候我们需要遍历a[1]和a[1]之前的所有元素并进行比较。设置一个变量j,用来记录第一个 比 a[1]元素小的那个元素的下标,也就是a[1]要插入的位置,这个时候跳出循环,并且没发现一个比a[1]大的元素,就要令这个元素后移一位。依次类推的算法直到整个数组的最后一个。
稳定性:稳定
时间复杂度:O(n^2)
空间复杂度:O(1)
代码:
public static void insertionSortt(int[] array){ //从a[1]开始 for(int i = 1; i < array.length; i++){ int currentElement = array[i]; int j; //标记元素要移动到的位置 //先判断currentElement前面一个数,如果要移动,移动后再判断前面一个数,直到判断到不需要移动或已经判断到list[0] for(j = i - 1; j >=0 && array[j] > currentElement; j--){ //将currentElement前面一个数向后移动一位 array[j + 1] = array[j]; } array[j + 1] = currentElement; } }
4、归并排序
动画演示:http://liveexample.pearsoncmg.com/dsanimation/MergeSortNeweBook.html
思想:
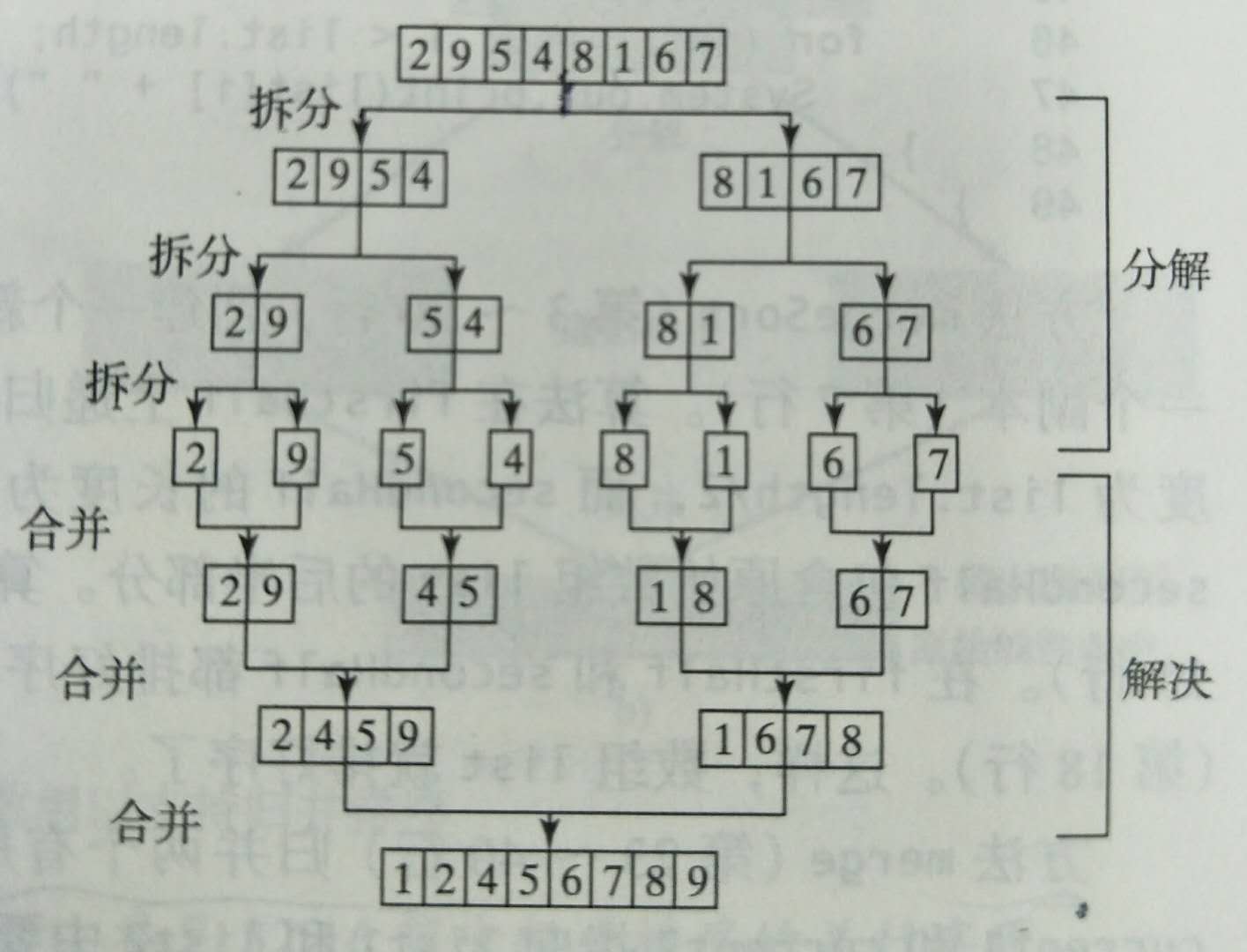
使用分而治之法对数组排序。将数组分为两半,对每部分递归地应用归并排序。在两部分都排好序后,对它们进行归并。
稳定性:稳定
时间复杂度:O(nlogn)
空间复杂度:O(n)
代码:
public static void mergeSort(int[] array) { if (array.length > 1) { // 创建临时数组firstHalf存放前面一半的元素 int[] firstHalf = new int[array.length / 2]; System.arraycopy(list, 0, firstHalf, 0, array.length / 2); // 递归 mergeSort(firstHalf); // 创建临时数组secondHalf存放后面一半的元素 int lengthOfSecondHalf = array.length - array.length / 2; int[] secondHalf = new int[lengthOfSecondHalf]; System.arraycopy(array, array.length / 2, secondHalf, 0, lengthOfSecondHalf); // 递归 mergeSort(secondHalf); // 归并到原始数组array中 merge(firstHalf, secondHalf, array); } } /** 归并 */ public static void merge(int[] array1, int[] array2, int[] temp) { /* * 归并两个有序数组array1、array2为一个临时数组temp。 * current1和current2指向array1和array2中要考虑的当前元素,重复比较array1和array2中的当前元素,并将较小的一个元素移动到temp中。 * 如果较小元素在array1中,current1增加1;如果较小元素在array2中,current2增加1。 * 最后array1或array2会剩余一个元素没有移动,将它直接复制到temp中。 */ int current1 = 0;// array1中要考虑的当前元素 int current2 = 0;// array2中要考虑的当前元素 int current3 = 0;// temp中要考虑的当前元素 while (current1 < array1.length && current2 < array2.length) { // 如果较小元素在array1中,current1增加1 if (array1[current1] < array2[current2]) temp[current3++] = array1[current1++]; // 如果较小元素在array2中,current2增加1 else temp[current3++] = array2[current2++]; } while (current1 < array1.length) temp[current3++] = array1[current1++]; while (current2 < array2.length) temp[current3++] = array2[current2++]; }
5、快速排序
动画演示:http://liveexample.pearsoncmg.com/dsanimation/QuickSortNeweBook.html
思想:
在数组中选择一个基准元素(pivot),将数组分为两部分,使得第一部分中的所有元素都小于等于pivot,第二部分的所有元素都大于pivot。
对第一部分递归的应用快速排序算法,然后对第二部分递归的应用快速排序算法。
稳定性:不稳定
时间复杂度:O(nlogn),最坏时间复杂度O(n^2)
空间复杂度:O(logn)
代码:
/**快速排序算法*/ public static void quickSort(int[] data, int start, int end) throws Exception{ if(start >= end) return; //分而治之 int index = partition(data, start, end); if(index > start) quickSort(data, start, index - 1); if(index < end) quickSort(data, index + 1, end); } /**重要*/ //选择一个基准元素,把data中比基准元素小的数字移到其左边,比基准元素大的数字移到其右边。并返回移动后基准元素下标 public static int partition(int[] data, int low,int high) throws Exception{ if(data == null || low < 0 || high >= data.length) throw new Exception("Invalid Parameters"); //选择第一个数作为基准元素 int pivot = data[low]; while(low < high){ //从右向左找小于基准元素的值 //注意一定要加等号,不然可能会出现死循环 while(low < high && data[high] >= pivot) high--; data[low] = data[high];//赋值 //从左向右找大于基准元素的值 while(low < high && data[low] <= high) low++; data[high] = data[low]; } //此时low与high在同一个位置,把pivot的值给low data[low] = pivot; return low; }
6、堆排序
动画演示:http://liveexample.pearsoncmg.com/dsanimation/HeapeBook.html
堆排序使用一个二叉堆,它首先将所有的元素添加到一个堆上,然后不断移除最大的元素以获得一个排好序的线性表。
堆排序使用一个二叉堆,该二叉堆是一个完全二叉树,该二叉树具有如下属性:
- 形状:是一个完全二叉树。(如果一棵二叉树的每层都是满的,或者最后一层没填满并且最后一层的叶子都是靠最左放置的,那么这棵二叉树就是完全的。)
- 堆属性:每个结点大于或等于它的任意一个孩子。
给堆添加一个结点:
首先将它添加到堆的末尾;
将最后一个结点作为当前节点; while(当前结点大于它的父节点){ 将当前结点和它的父节点交换; }从对中删除最大元素,即删除根节点:
将最后一个结点替换根结点; 让根结点成为当前结点; while(当前结点具有子节点并且当前结点小于它的子结点){ 将当前结点和它的子节点交换; }这样堆排序的步骤:首先使用Heap创建一个对象,使用add方法将所有元素添加到堆中,然后使用remove方法从堆中删除所有元素,记录删除的元素就是一个有序数组了。
稳定性:不稳定。
时间复杂度:O(nlogn)
设h表示n个元素的堆的高度。由于堆是一颗完全二叉树,所以第一层有1(2^0)个结点,第二层有2(2^1)个结点,....,第h层有2^(h-1)个结点,最后第h+1层最少有1个最多有2^h个结点。因此
1+2+...+2^(h-1)< n <= 1+2+...+2^(h-1)+2^h,即2^h < n+1 <= 2^(h+1),
所以h < log(n+1) <= h+1。所以堆的高度为O(logn)。
由于add方法会最追踪从叶子结点到根节点的路径,因此向堆中添加一个新元素最多需要h步,所以建立一个包含n个元素的数组的初始堆需要O(nlogn)时间。因为remove方法要追踪从根节点到叶子结点的路径,因此从堆中删除根节点后重建堆最多需要n步。由于要调用n次remove方法,所以由堆产生一个有序数组需要时间为O(nlogn)。
空间复杂度:O(1)。只是需要一个临时变量来交换元素位置,所以空间复杂度O(1)。
代码:
public static void heapSort(int[] array) { Heap<Integer> heap = new Heap(); //使用add方法将所有元素添加到堆中 for(int i = 0; i < array.length; i++) heap.add(array[i]); //然后使用remove方法从堆中删除所有元素。 以降序删除这些元素,得到的结果就是升序的 for(int i = array.length - 1; i >= 0; i--) array[i] = heap.remove(); } ---------------------------------------------------------------------------------- /**建一个堆类*/ class Heap<E extends Comparable<E>> { //利用list存结点,则根节点下标为0, 下标为i的父节点下标应为(i-1)/2,子节点应为2*i+1、2*i+2 private ArrayList<E> list = new ArrayList<E>(); //构造方法 public Heap() {} /**向堆中添加元素*/ public void add(E item) { //首先将它添加到堆的末尾 list.add(item); //将最后一个结点作为当前结点 int currentIndex = list.size() - 1; while(currentIndex > 0) { //父节点 int parentIndex = (currentIndex - 1) / 2; //当当前节点大于它的父节点时,将当前节点和它的父节点交换 if(list.get(currentIndex).compareTo(list.get(parentIndex)) > 0) { E temp = list.get(currentIndex); list.set(currentIndex, list.get(parentIndex)); list.set(parentIndex, temp); //currentIndex移到上一层 currentIndex = parentIndex; }else { break; } } } /**删除堆中的最大元素(删除根节点)*/ public E remove() { if(list.size() == 0) return null; E removeItem = list.get(0); //用最后一个结点替换根结点,并删除这个最大结点(原来的根结点) list.set(0, list.get(list.size() - 1)); list.remove(list.size() - 1); //让根节点成为当前结点 int currentIndex = 0; //当当前结点具有子结点并且当前结点小于它的子结点时,将当前结点和它较大的子结点交换 while(currentIndex < list.size()) { int leftIndex = currentIndex * 2 + 1;//左孩子结点 int rightIndex = currentIndex * 2 + 2;//右孩子结点 if(leftIndex >= list.size()) break; //说明没有孩子结点 //取左孩子结点和右孩子结点最大的结点,然后与当前结点比较 int maxIndex = leftIndex; if(rightIndex < list.size()) { if(list.get(rightIndex).compareTo(list.get(leftIndex)) > 0) maxIndex = rightIndex; } if(list.get(currentIndex).compareTo(list.get(maxIndex)) < 0) { E temp = list.get(currentIndex); list.set(currentIndex, list.get(maxIndex)); list.set(maxIndex, temp); //currentIndex移到下一层 currentIndex = maxIndex; }else { break; } } return removeItem; } }