前言:
本文主要是介绍下在一个实际的机器学习系统中,该怎样对数据进行预处理。个人感觉数据预处理部分在整个系统设计中的工作量占了至少1/3。首先数据的采集就非常的费时费力,因为这些数据需要考虑各种因素,然后有时还需对数据进行繁琐的标注。当这些都有了后,就相当于我们有了元素的raw数据,然后就可以进行下面的数据预处理部分了。本文是参考的UFLDL网页教程:Data Preprocessing,在该网页的底部可以找到其对应的中文版。
基础知识:
一般来说,算法的好坏一定程度上和数据是否归一化,是否白化有关。但是在具体问题中,这些数据预处理中的参数其实还是很难准确得到的,当然了,除非你对对应的算法有非常的深刻的理解。下面就从归一化和白化两个角度来介绍下数据预处理的相关技术。
数据归一化:
数据的归一化一般包括样本尺度归一化,逐样本的均值相减,特征的标准化这3个。其中数据尺度归一化的原因是:数据中每个维度表示的意义不同,所以有可能导致该维度的变化范围不同,因此有必要将他们都归一化到一个固定的范围,一般情况下是归一化到[0 1]或者[-1 1]。这种数据归一化还有一个好处是对后续的一些默认参数(比如白化操作)不需要重新过大的更改。
逐样本的均值相减主要应用在那些具有稳定性的数据集中,也就是那些数据的每个维度间的统计性质是一样的。比如说,在自然图片中,这样就可以减小图片中亮度对数据的影响,因为我们一般很少用到亮度这个信息。不过逐样本的均值相减这只适用于一般的灰度图,在rgb等色彩图中,由于不同通道不具备统计性质相同性所以基本不会常用。
特征标准化是指对数据的每一维进行均值化和方差相等化。这在很多机器学习的算法中都非常重要,比如SVM等。
数据白化:
数据的白化是在数据归一化之后进行的。实践证明,很多deep learning算法性能提高都要依赖于数据的白化。在对数据进行白化前要求先对数据进行特征零均值化,不过一般只要 我们做了特征标准化,那么这个条件必须就满足了。在数据白化过程中,最主要的还是参数epsilon的选择,因为这个参数的选择对deep learning的结果起着至关重要的作用。
在基于重构的模型中(比如说常见的RBM,Sparse coding, autoencoder都属于这一类,因为他们基本上都是重构输入数据),通常是选择一个适当的epsilon值使得能够对输入数据进行低通滤波。但是何谓适当的epsilon呢?这还是很难掌握的,因为epsilon太小,则起不到过滤效果,会引入很多噪声,而且基于重构的模型又要去拟合这些噪声;epsilon太大,则又对元素数据有过大的模糊。因此一般的方法是画出变化后数据的特征值分布图,如果那些小的特征值基本都接近0,则此时的epsilon是比较合理的。如下图所示,让那个长长的尾巴接近于x轴。该图的横坐标表示的是第几个特征值,因为已经将数据集的特征值从大到小排序过。
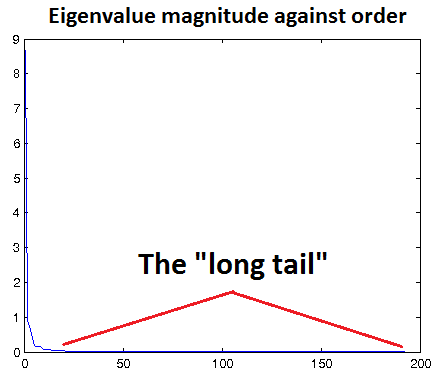
文章中给出了个小小的实用技巧:如果数据已被缩放到合理范围(如[0,1]),可以从epsilon = 0.01或epsilon = 0.1开始调节epsilon。
基于正交化的ICA模型中,应该保持参数epsilon尽量小,因为这类模型需要对学习到的特征做正交化,以解除不同维度之间的相关性。(暂时没看懂,因为还没有时间去研究过ICA模型,等以后研究过后再来理解)。
教程中的最后是一些常见数据的预处理标准流程,其实也只是针对具体数据集而已的,所以仅供参考。
参考资料: