前言:
这是coursera课程:Probabilistic Graphical Models 上的第二个实验,主要是用贝叶斯网络对基因遗传问题进行一些计算。具体实验内容可参考实验指导教材:bayes network for genetic inheritance. 大家可以去上面的链接去下载实验材料和stard code,如实验内容有难以理解的地方,欢迎私底下讨论。下面是随便写的一些笔记。
完成该实验需要了解一些遗传方面的简单知识,可参考:Introduction to heredity(基因遗传简单介绍)
关于实验的一些约定和术语:
同位基因(也叫等位基因)中有一个显现基因(dominant allele)和一个隐性基因(recessive allele)。
homozygous:纯合体
heterozygous:杂合体
一个factor表不仅可以表示联合概率,也可以表示条件概率,这里约定规则是: 最左边的那个元素表示条件输出,即它是在后面元素出现条件下的输出。
关于变量的命名,因为在图模型中,会出现很多变量,这些变量在实际编程中是要取名字的,一般是按照某种顺序规则来取,本次实验的规则是:依照家谱图中每个人的名字依次取,假设有k个人,则每个人对应了2个factor,所以前k个变量表示这k个人的基因型标量,后k个变量表示这k个人的表现型变量。如果把每个人的基因对应的2个染色体分开考虑,则需要3k个变量,前k个表示每个人的第一条染色体对应处的基因,中间k个表示每个人的第二条染色体对应处的基因,后k个变量和以前的一样,表示这k个人的表现型变量。
程序中的alleleFreqs是个n*1的向量,n为单个等位基因的个数。
程序中的alphaList是个m*1的向量,m为2个等位基因组合的个数。
例如,某个基因家谱图可如下:
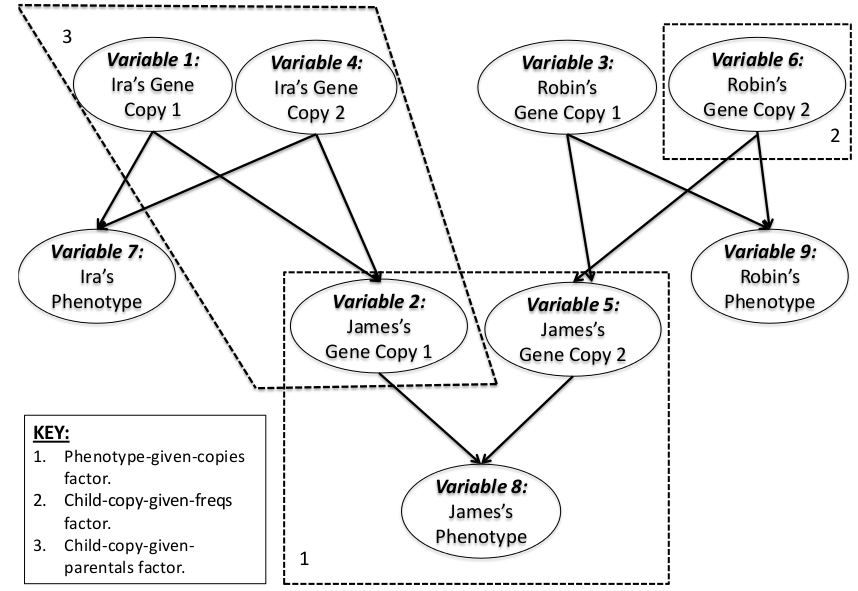
matlab知识:
matlab在使用元胞数组时,需要先用cell来定义大小。对元胞使用小括号访问时返回的是对应位置的数据类型,而不是其内容,要想得到其内容,需要用大括号访问。
结构体的定义要么直接对其赋值,这时候需调用其field,要么用关键字struct来定义。
tf = isfield(S, 'fieldname'):
tf=1表示结构体成员S中含有变量fieldname.
实验中的一些函数:
phenotypeFactor = phenotypeGivenGenotypeMendelianFactor(isDominant, genotypeVar, phenotypeVar):
练习1需要完成的内容。该函数功能是生成一个factor,该factor每一项是一个条件概率,表示在基因类型变量(genotypeVar)下的表现类型(phenotypeVar)的概率,即P(person’s phenotype | person’s genotype)。其概率值是按照孟德尔模型(mendelian model)来分配的。
v = GetValueOfAssignment(F, A):
得到facotr F在assignment A处的值。
F = SetValueOfAssignment(F, A, v):
该函数实现对factor F的一个assignment对应的值进行更新,更新后的值为v.注意一定要将这个函数的返回值赋给F才有效。
phenotypeFactor = phenotypeGivenGenotypeFactor(alphaList, genotypeVar, phenotypeVar):
练习2需要完成的内容。这个函数也是实现表现型在基因型下的条件概率,但此时概率不一定为0或者1,因为不严格满足孟德尔模型,所以参数列表中多了一个alphaList变量,该变量存储的是各种基因型下出现某种病的概率值。genotypeVar, phenotypeVar分别为基因类型变量和表现型变量,仅仅是个变量名而已。
[allelesToGenotypes,genotypesToAlleles]= generateAlleleGenotypeMappers(numAlleles):
numAlleles为等位基因的个数,假设个数为n,则allelesToGenotypes为一个n*n的矩阵,代表的是2不同等位基因组合后的编码(行号和列号分别代表这2个基因序号),因为这个编码矩阵是对称的,所以只有m=n*(n-1)/2+n个编码。genotypesToAlleles为一个m*2大小的矩阵,每一行的两个元素代表该基因编码下的2个基因序号。
[allelesToGenotypes,genotypesToAlleles]= generateAlleleGenotypeMappers(numAlleles):
用同位基因的个数numAlleles作为参数,来产生2个矩阵。其中allelesToGenotypes(i,j)表示编号为i的同位基因和编号为j的同位基因在基因类型(每个基因类型由2个基因构成)中的序号。 genotypesToAlleles由2列构成,每一行对应一个基因类型的序号,这2个列元素表示该基因序列对应的2个同位基因的编号。
genotypeFactor = genotypeGivenAlleleFreqsFactor(alleleFreqs, genotypeVar):
练习3需要完成的内容。某个基因可能有多个等位基因,而每个等位基因的概率不同,概率值保存在alleleFreqs中。这个函数的作用就是由这些等位基因组合产生的每个基因类型的概率,这相当于一个先验分布,因为没有去考虑由父母亲的基因交叉得到下一代。genotypeVar表示这个基因类型的变量名。
genotypeFactor=genotypeGivenParentsGenotypesFactor(numAlleles, genotypeVarChild, genotypeVarParentOne, genotypeVarParentTwo):
练习4需要完成的内容。该函数的作用是已知父亲和母亲某个等位基因的分布,求出儿子对应基因的概率分布。其中numAlleles是等位基因的个数,genotypeVarChild, genotypeVarParentOne, genotypeVarParentTwo分别表示儿子,父亲,母亲对应的基因变量。输出的genotypeFactor是一个变量值val为3维矩阵的factor. 这个函数与上面那个函数不同,这里的输出factor是在考虑了父母亲factor情况下的。
factorList = constructGeneticNetwork(pedigree, alleleFreqs, alphaList):
练习5需要完成的内容。在给定家谱(家谱中包含了成员的名字,父母亲等信息)pedigree、等位基因的概率分布alleleFreqs、不同基因组合导致生并的概率分布alphaList后,就可以求出这个家庭中每个成员的2个factor:一个是关于自己的基因类型的,这由其父母亲的基因类型决定;另一个是关于自己的表现类型的,这与他的基因类型有关。在完成该函数的代码中会调用前面的函数genotypeGivenAlleleFreqsFactor(), genotypeGivenParentsGenotypesFactor(), phenotypeGivenGenotypeFactor().所以前面很多工作都是为后面服务的。
phenotypeFactor=phenotypeGivenCopiesFactor(alphaList, numAlleles, geneCopyVarOne, geneCopyVarTwo, phenotypeVar):
练习6所需完成的内容。geneCopyVarOne和geneCopyVarTwo一个来自母亲的基因,一个来自父亲的的基因。phenotypeVar为下一代表现型标量。该函数的作用是给定来自父母亲的2个基因,求这个组合下的下一代出现病的概率,当然了,因为不服从孟德尔模型,所以还需要参考概率值alphaList.
geneCopyFactor = childCopyGivenFreqsFactor(alleleFreqs, geneCopyVar):
该函数的作用是得获得染色体中一个等位基因的概率,该概率来源于通用的先验alleleFreqs. 该factor表格大小为n*1.
geneCopyFactor = childCopyGivenParentalsFactor(numAlleles, geneCopyVarChild, geneCopyVarOne, geneCopyVarTwo):
该函数的作用也是得获得染色体中一个等位基因的概率,只是这取决于父母亲各自那个等位基因。所以这个factor表格大小为n*3,且每个条件概率只可能取3个 值:0, 0.5, 1.
factorList = constructDecoupledGeneticNetwork(pedigree, alleleFreqs, alphaList):
实验7所需完成内容。该函数是构造Decoupled的贝叶斯网络,这里的Decoupled是指家谱中每个人染色体的2个等位基因分布来考虑。所以每个人都对应有3个factor,一个是基因1的概率,n*3大小(如果家谱中没有父母亲,则是n*1大小),一个是基因2的概率,n*3大小(如果家谱中没有父母亲,则是n*1大小),另一个是对应的表现型分布2n^2*3大小。
phenotypeFactor=constructSigmoidPhenotypeFactor(alleleWeights, geneCopyVarOneList, geneCopyVarTwoList, phenotypeVar):
这是练习8的内容。一种病可能由多个基因决定,而每个基因又可能有多个等位基因。这里的alleleWeights矩阵中alleleWeights{i}(j)表示的意思是第i个基因的第j号等位基因对这种病的影响权值。当把某种病对应的所有基因的等位基因权值都考虑进来,那么得这种病的概率则与这些权值之和有关,本实验假设它们最后的关系是服从sigmoid分布。geneCopyVarOneList和geneCopyVarTwoList都是列向量(因为一种病可能由多个基因决定),所以在计算phenotypeFactor.var时需要这2个向量转置。
课件中的一些内容:
贝叶斯推理的3种形式:因果推理,证据推理,内部因果推理(注意explean away现象)。
active trail(路径中不能出现V型结构,除非V型中间节点或者其子孙节点被观测到)。
变量之间的独立性判断、条件独立性判断(可以通过联合概率与某2个factor的乘积的关系来判断)。
一个图能够被因式分解,则有可能推导出独立性。如果有D-separation,则一定可以推导出独立性。
分布P能够分解图G ,则G是P的一个I-map,反之,如果G是P的一个I-map,则P能分解G.
为了简化时序模型,一般会有马尔科夫和时序不变性这2个假设。
时序转移模型(Template Transition Model),可以包含内部时序转移和外部时序转移。
Ground Network(unrolled network)指的是不同时间内的结构依次复制。
2TBN是一个动态贝叶斯网络,它有一个初始化以及unrolled network,所以有2个转移概率。
HMM中的状态转移概率是稀疏的。
Plate model可以嵌套,可以重叠
参考资料: