KMP 算法（转载于SYC巨巨%%%）

原文链接：膜大佬orz

首先我们说一下什么是KMP算法

这里贴上百度百科上的解释：

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现，因此人们称它为克努特——莫里斯——普拉特操作（简称KMP算法）。KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数，函数本身包含了模式串的局部匹配信息。时间复杂度O(m+n)。

首先我们看一下直接暴力解字符串匹配：

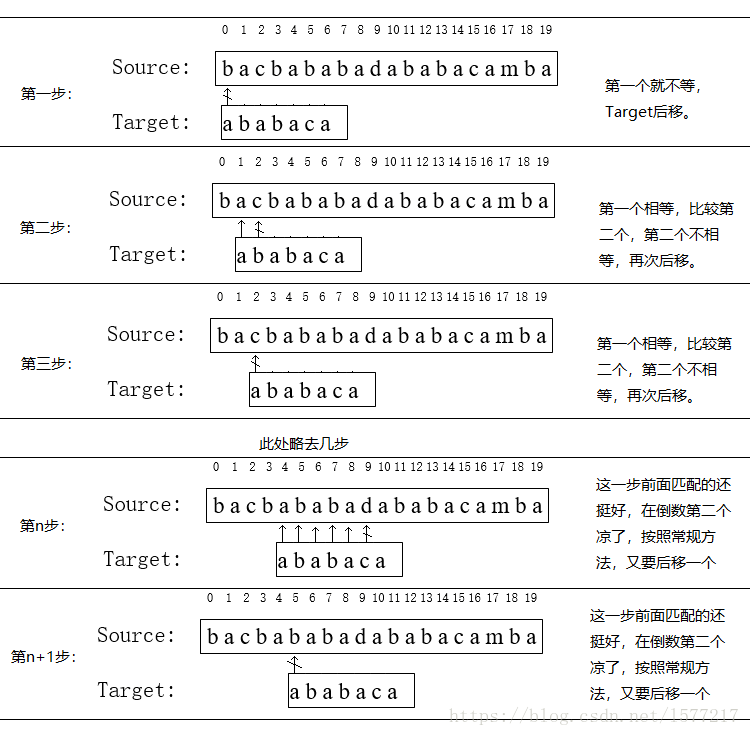
代码实现：

    int ViolentMatch(char* s, char* p)  
    {  
        int sLen = strlen(s);  
        int pLen = strlen(p);  
      
        int i = 0;  
        int j = 0;  
        while (i < sLen && j < pLen)  
        {  
            if (s[i] == p[j])  
            {  
                //①如果当前字符匹配成功（即S[i] == P[j]），则i++，j++      
                i++;  
                j++;  
            }  
            else  
            {  
                //②如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0      
                i = i - j + 1;  
                j = 0;  
            }  
        }  
        //匹配成功，返回模式串p在文本串s中的位置，否则返回-1  
        if (j == pLen)  
            return i - j;  
        else  
            return -1;  
    }  

毫无疑问这样的复杂度巨鸡儿高随便卡翻你O（n*m）//n是source串的长度，m是Target串的长度

但是KMP算法则可以将复杂度降到O（M+n）

KMP算法的难理解之处与本文叙述的约定

在继续我们的讲述之前，首先讲一下为什么KMP算法不是很好理解。
虽然说网上关于KMP算法的博客、教程很多，但查阅了很多资料，

详细讲述过程及原理的不多，真正讲得好的文章在定义方面又有细微的不同（当然，真正写得好的文章也有，这里就不一一列举），

比如说有些从1开始标号，有些next表示的是前一个而有些是当前的，通读下来，难免会混乱。
那么，为了防止读者在接下来的内容中感到和笔者之前学习时同样的困惑，

在这里先对下文做一些说明和约定。

///1.本文中，所有的字符串从0开始编号
///2.本文中，F数组（即其他文章中的next），F[i]表示0~i的字符串的最长相同前缀后缀的长度。

F数组的运用

那么现在假设我们已经得到了F的所有值，我们如何利用F数组求解呢？
我们还是先给出一个例子（笔者用了好长时间才构造出这一个比较典型的例子啊）：
A="abaabaabbabaaabaabbabaab"
B="abaabbabaab"
当然读者可以通过手动模拟得出只有一个地方匹配
abaabaabbabaaabaabbabaab
那么我们根据手动模拟，同样可以计算出各个F的值

B="a b a a b b a b a a b "
F= 0 0 1 1 2 0 1 2 3 4 5

我们再用i表示当前A串要匹配的位置（即还未匹配），j表示当前B串匹配的位置（同样也是还未匹配），补充一下，若i>0则说明i-1是已经匹配的啦（j同理）。
首先我们还是从0开始匹配：

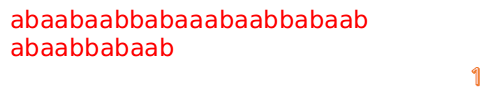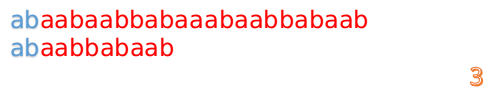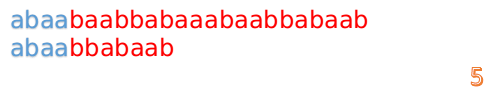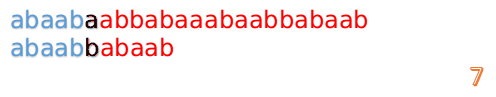
此时，我们发现，A的第5位和B的第5位不匹配（注意从０开始编号），此时i=5,j=5，那么我们看F[j-1]的值：

F[5-1]=2;

这说明我们接下来的匹配只要从B串第２位开始（也就是第３个字符）匹配，因为前两位已经是匹配的啦，具体请看图

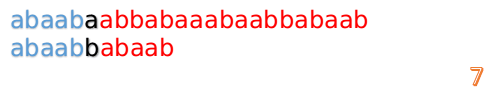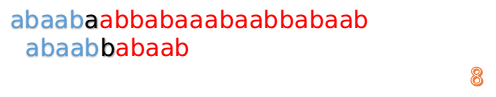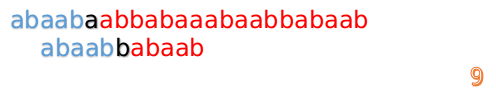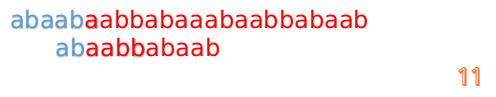
继续进行

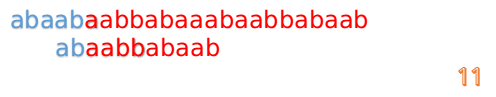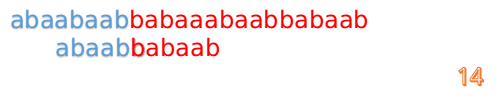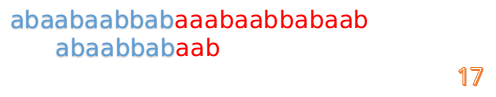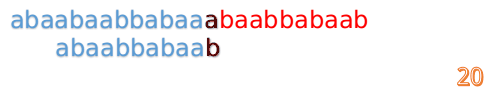
我们又发现，A串的第13位和B串的第10位不匹配，此时i=13,j=10，那么我们看F[j-1]的值：

F[10-1]=4

这说明B串的0~3位是与当前(i-4)~(i-1)是匹配的，我们就不需要重新再匹配这部分了，把B串向后移，从Ｂ串的第４位开始匹配：

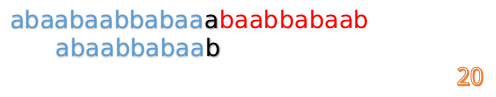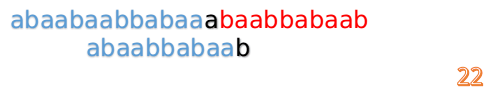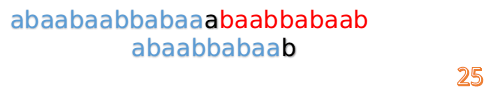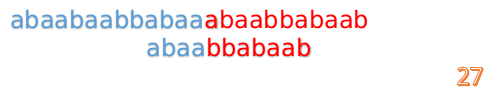
这时我们发现A串的第13位和B串的第4位依然不匹配

此时i=13,j=4，那么我们看F[j-1]的值：

F[4-1]=1

这说明B串的第0位是与当前i-1位匹配的，所以我们直接从B串的第1位继续匹配：

但此时B串的第1位与A串的第13位依然不匹配

此时，i=13,j=1,所以我们看一看F[j-1]的值:

F[1-1]=0

好吧，这说明已经没有相同的前后缀了，直接把B串向后移一位，直到发现B串的第0位与A串的第i位可以匹配（在这个例子中，i=13）

再重复上面的匹配过程，我们发现，匹配成功了！

这就是KMP算法的过程。
另外强调一点，当我们将B串向后移的过程其实就是i++,而当我们不动B，而是匹配的时候，就是i++,j++，这在后面的代码中会出现，这里先做一个说明。

最后来一个完整版的：

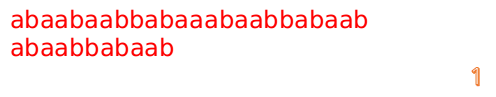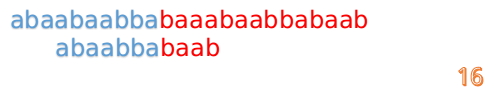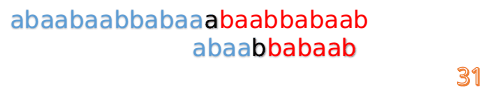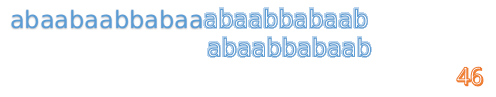
F数组的求解

既然已经用这么多篇幅具体阐述了如何利用F数组求解，那么如何计算出F数组呢？总不能暴力求解吧。

KMP的另外一个巧妙的地方也就在这里，它利用我们上面用B匹配A的方法来计算F数组，简单点来说，就是用B串匹配B串自己！
当然，因为B串==B串，所以如果直接按上面的匹配，那是毫无意义的（自己当然可以完全匹配自己啦），所以这里要变一变。

因为上面已经讲过一部分了，先给出计算F的代码：

inline void GetNext(string s)//获得字符串s的next数组
{
    int l=s.length(),t;
    Next[0]=-1;//如果在0位置失配则是向下移动一位
    for(int i=1;i<l;++i)//依次求解后面的next数组
    {
        t=Next[i-1];
        while(s[t+1]!=s[i]&&t>=0)//循环求解next值 
            t=Next[t];
        if(s[t+1]==s[i])//如果是匹配上而退出循环 
            Next[i]=t+1;
        else            //否则则是匹配不上 
            Next[i]=-1; //指向头 
    }
}

最后是全部的算法：

inline void KMP(string s1,string s2)
{
    GetNext(s2);
    int l1=s1.length();
    int l2=s2.length();
    int i=0,j=0;
    while(j<l1)
    {
        if(s2[i]==s1[j])//当前位匹配成功，继续匹配下一位
        {
            ++i;++j;
            if(i==l2)//完全匹配
            {
                Ans.push_back(j-l2+1);//储存答案
                i=Next[i-1]+1;//继续匹配                
            }
        }
        else
        {
            if(i==0)//在首位不匹配
                j++;//直接向后挪一位
            else
                i=Next[i-1]+1;//跳转
        }
    }
}