(Manacher) 算法总结
一、用途
-
解决关于一个字符串中回文子串的问题,最经典的应用就是求一个字符串中的最长的回文子串长度。
-
例题:洛谷P3805
-
(nle 1.1*10^7)
-
对于这样的问题,我们可以想到枚举每一个位置作为回文串的中心,然后二分能延伸的最长长度,直接哈希检验,但这样的复杂度是(mathcal O(nlog(n))),无法通过此题,我们需要一个更快的算法:这就是(manachar)算法了。
二、算法流程:
- 我们依然考虑通过回文串的中心来寻找回文串,但是观察以下两种字符串:(aabaa)与(aaaa),二者都是回文的,但它们的对称中心不同,前者的中心是(b),后者的中心在两个(a)之间,这会导致记录回文中心十分困难,因此我们可以在每两个之间插入一个像'#'一样的字符,这样所有的字符串的中心就都是字符了,同时为了区分边界,我们在字符串最前添加一个'$'
scanf("%s",s+1);len=strlen(s+1);
t[++n]='$';
for(int j=1;j<=len;++j){
t[++n]='#';
t[++n]=s[j];
}
- 考虑(p[i])为新字符串中以(i)为对称中心的最长回文串的半径,那么显然除去‘#‘后(p[i]-1)就是原字符串中最长的回文串长度
- 接下来,我们做出一个神奇的操作,定义(mid)与(r)表示目前找到的所有回文串的右边界中最远的一个是(r),这个回文串的中心是(mid)、
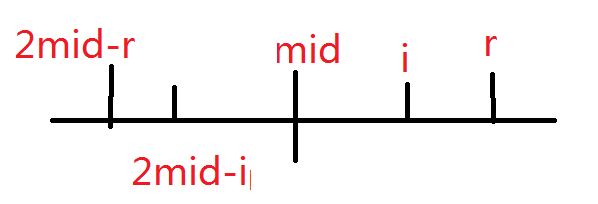
- 考虑我们现在正在计算(p[i]),且(i)在(mid)与(r)之间,假设(j=2mid-i)为(i)关于(mid)的对称点
-
那么根据回文子串的性质,([j-p[j]+1,j+p[j]+1])是一个回文串,又因为对称性,于是([j-p[j]+1,j+p[j]-1]=[i-p[j]+1,i+p[j]-1])
-
但当(i+p[i]-1>r)是,后一条对称性就不成立了,于是(p[i]=min(p[j],r-i+1)),就得到了一个最小的回文串长度,因此我们节省了大量时间
-
接下来再暴力看能否继续拓展即可
-
求出(p[i])后再看能否更新(r)就完了,这就是(manacher)的全过程了:
#include<bits/stdc++.h> using namespace std; const int N=2.2e7+100; char s[N],t[N]; int len,n,ans,p[N]; int main(){ scanf("%s",s+1);len=strlen(s+1); t[++n]='$'; for(int j=1;j<=len;++j){ t[++n]='#'; t[++n]=s[j]; } t[++n]='#'; for(int i=1,mid=0,r=0;i<=n;++i){ if(mid<=i&&i<=r) p[i]=min(p[2*mid-i],r-i+1); while(t[i-p[i]]==t[i+p[i]]) ++p[i]; if(i+p[i]-1>r) r=i+p[i]-1,mid=i; ans=max(ans,p[i]); } printf("%d ",ans-1); return 0; } -
那么问题来了,为什么这个如此简单的算法居然达到了线性复杂度?
-
因为我们始终保证(r)是最右边的回文串端点,所以暴力拓展时,要么(j)的回文串左端点越界,要么(i)越界,此时(i)的回文串右端一定超出(r),于是每次暴力拓展一定会更新一次(r),于是暴力拓展就相当于将(r)移动到最右侧,只会进行(mathcal O(n)),于是总复杂度是(mathcal O(n))的
三、其他应用
- 洛谷P1659
- 题目要求长度前(k)大的奇回文串长度之积
- 注意到当我们通过(manacher)求出以(i)为中心的最长回文串半径为(p[i])时,意味着以(i)为中心的回文串半径可以为(1-p[i]),进而我们就能得出对于任意的(i),半径为(i)的回文串的数量了:
#include<bits/stdc++.h>
using namespace std;
const int mod=19930726;
const int N=1e6+10;
typedef long long ll;
int n,p[N];
char s[N];
ll pos[N],mx,k;
inline int ksm(int a,ll b){
int ret=1;
for(;b;b>>=1,a=1ll*a*a%mod) (b&1)&&(ret=1ll*ret*a%mod);
return ret;
}
int main(){
// freopen("in.in","r",stdin);
scanf("%d%lld",&n,&k);
scanf("%s",s+1);
s[0]='$';s[n+1]='#';
for(int i=1,mid=0,r=0;i<=n;++i){
if(mid<=i&&i<=r) p[i]=min(p[2*mid-i],r-i+1);
while(s[i-p[i]]==s[i+p[i]]) ++p[i];
if(i+p[i]-1>r) r=i+p[i]-1,mid=i;
pos[p[i]]++;
mx=max(mx,1ll*p[i]);
}
int ans=1;
for(int i=mx;i>=0;--i){
pos[i]+=pos[i+1];
if(pos[i]<k){
k-=pos[i];
ans=1ll*ans*ksm(2*i-1,pos[i])%mod;
}
else{
ans=1ll*ans*ksm(2*i-1,k)%mod;
k=0;
break;
}
}
if(k) puts("-1");
else printf("%lld
",ans);
return 0;
}
-
显然我们可以将(S)每两个字母间隔中插入'#'后,考虑求出对于第(i)位,(l[i])表示以(i)为开头的最长回文串长度与(r[i])表示以(i)为结尾的最长回文串长度加起来,然后枚举‘#’将它的(l[i])与(r[i])加起来更新答案即可。
-
考虑如何求这个,首先在(manacher)求(p[i])过程中,我们通过求出来的以每个点为中心的最长回文串的长度更新其左右端点的信息,即:
l[i-p[i]+1]=max(l[i-p[i]+1],p[i]-1); r[i+p[i]-1]=max(r[i+p[i]-1],p[i]-1); -
但此时我们只更新了左右端点的位置,例如对于(ababa)我们只更新了最左侧与最右侧的(a)的答案,但(ababa)的子集(bab)也是回文串,它比(ababa)端两个字符,于是我们将左右端点分别向中间推,因为这道题我们只关心'#'位置的答案,所以我们每次推两个,即:
for(int i=2;i<=n;i+=2) l[i]=max(l[i],l[i-2]-2); for(int i=n;i>=2;i-=2) r[i]=max(r[i],r[i+2]-2); -
进而我们就能正确推出答案了:
#include<bits/stdc++.h> using namespace std; const int N=2e5+10; char s[N],t[N]; int len,n,l[N],r[N],p[N]; int main(){ scanf("%s",s+1); len=strlen(s+1); t[++n]='$'; for(int i=1;i<=len;++i){ t[++n]='#'; t[++n]=s[i]; } t[++n]='#'; for(int i=1,mid=0,R=0;i<=n;++i){ if(i>=mid&&i<=R) p[i]=min(p[2*mid-i],R-i+1); while(t[i-p[i]]==t[i+p[i]]) ++p[i]; if(i+p[i]-1>R) R=i+p[i]-1,mid=i; l[i-p[i]+1]=max(l[i-p[i]+1],p[i]-1); r[i+p[i]-1]=max(r[i+p[i]-1],p[i]-1); } for(int i=2;i<=n;i+=2) l[i]=max(l[i],l[i-2]-2); for(int i=n;i>=2;i-=2) r[i]=max(r[i],r[i+2]-2); int ans=0; for(int i=2;i<=n;i+=2) if(l[i]&&r[i]) ans=max(ans,l[i]+r[i]); printf("%d ",ans); return 0; }