1.什么是决策树
什么是决策树呢?首先我们生活中有很多决策树的例子,比如相亲T_T,很多妹子都会这样选择。
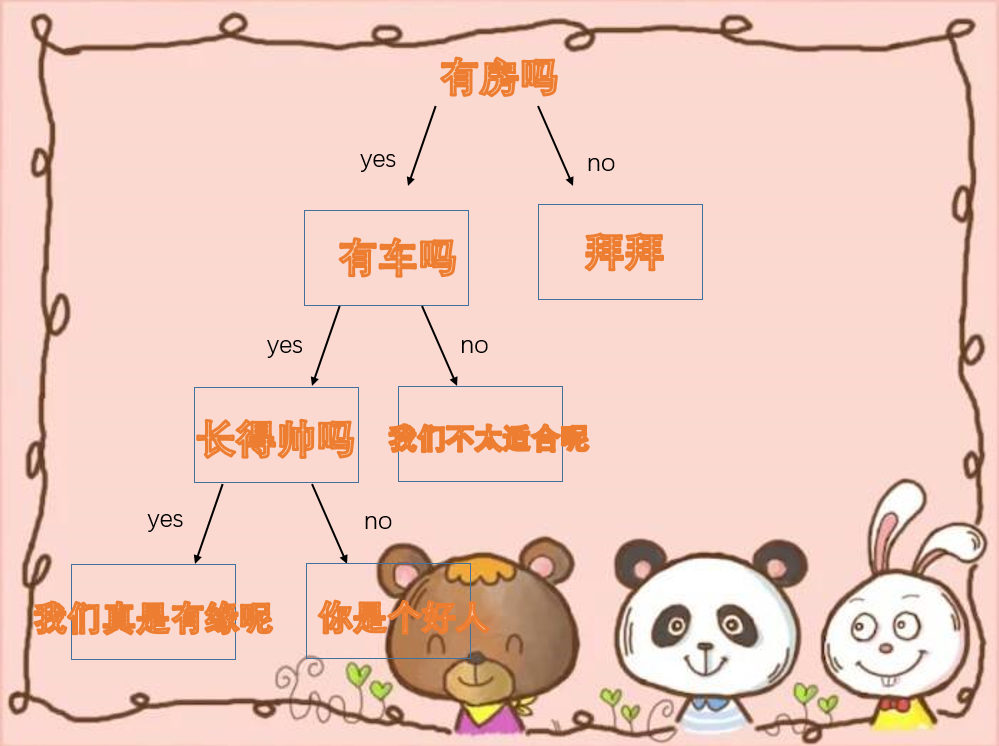
再比如说,某公司招聘机器学习算法工程师。
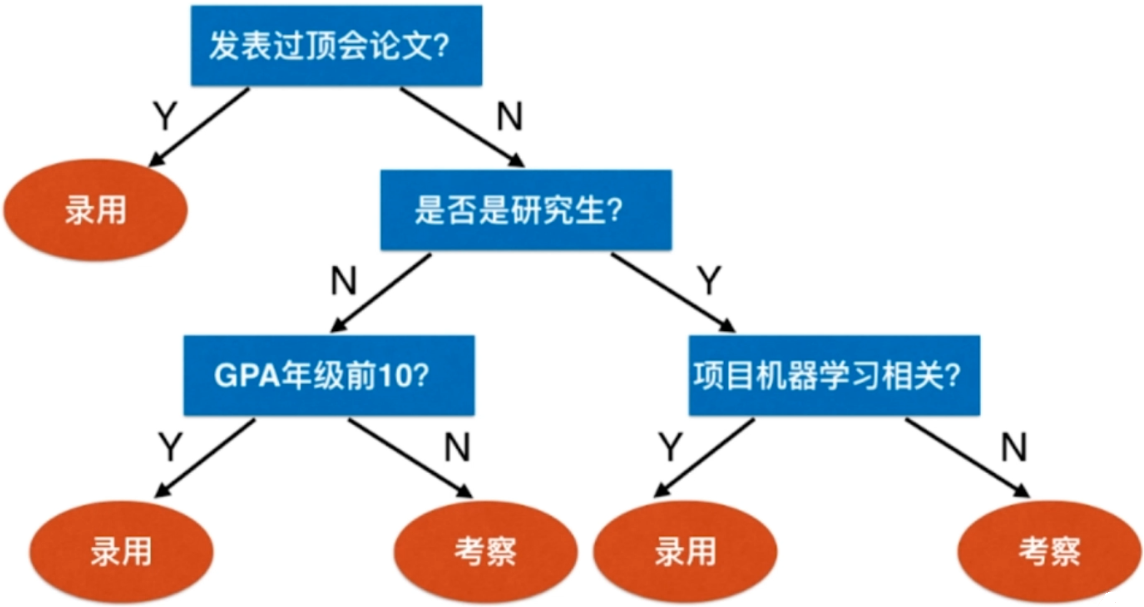
每一步都在进行一个决策,最终形成了一个倒立的树状结构,我们把这样一个过程称之为决策树。
我们在数据结构当中,也有树结构。这里的决策树同样具备树结构的属性。比如根节点,叶子节点。以及树的深度,当然这里就是3,因为我们通过简历对所有应聘者进行分析,决定是录用还是考察该应聘者,最终需要通过三次决策。
我们来看看sklearn中是如何使用决策树的,然后进一步认识决策树。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# 这里我们依旧是用鸢尾花数据集
iris = load_iris()
# 为了可视化,我们只选取两个特征,这里选择后两个特征
X = iris.data[:, 2:]
y = iris.target
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.scatter(X[y == 2, 0], X[y == 2, 1])
plt.show()
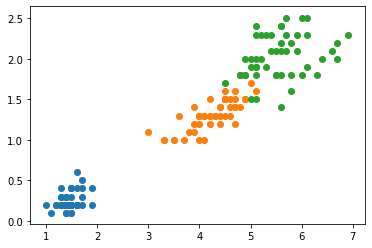
from sklearn.tree import DecisionTreeClassifier
# max_depth:树的深度
# criterion:评判标准,这里我们采用熵,至于什么是熵,后面介绍
dt_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy")
dt_clf.fit(X, y)
# 绘制决策边界
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(1, -1),
np.linspace(axis[3], axis[2], int((axis[3] - axis[2]) * 100)).reshape(1, -1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(["#EF9A9A", "#FFF59D", "#90CAF9"])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
plot_decision_boundary(dt_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.scatter(X[y == 2, 0], X[y == 2, 1])
plt.show()
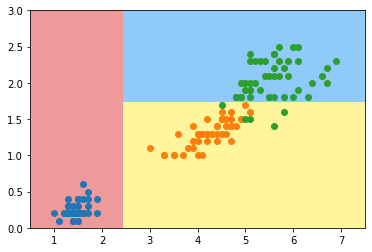
我们来对这个决策树进行分析,看看我们得到的是一个什么样的决策树。
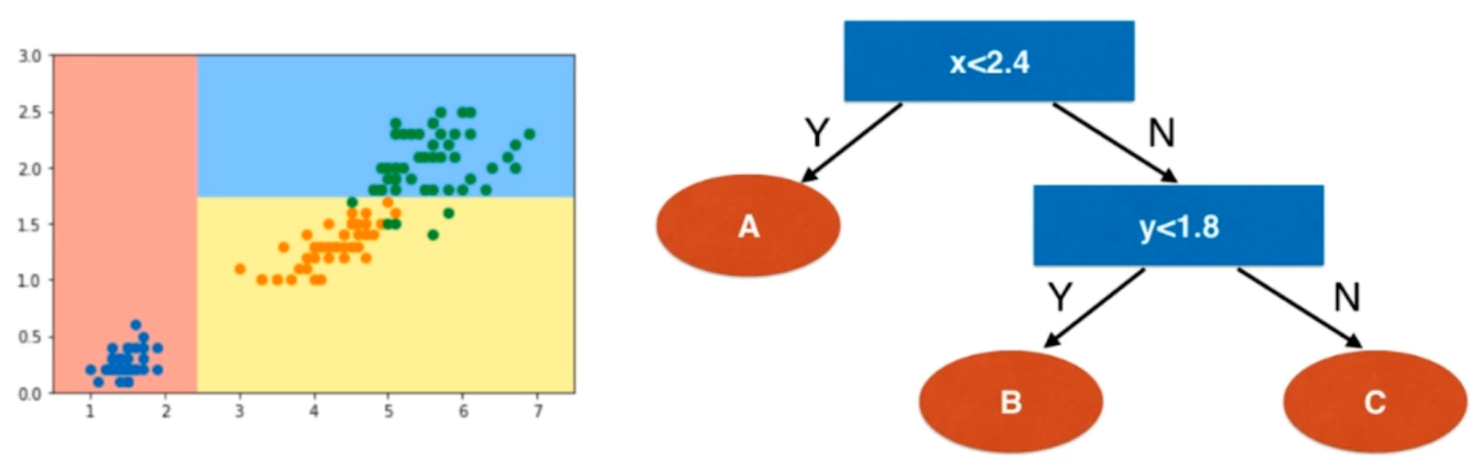
这个数字是大概估算出来的,总之就是一步一步的进行决策。由此我们总结出决策树的一些性质。
决策树是一个非参数学习算法可以解决分类问题并且和knn一样,天然解决多分类问题。和knn一样,也可以解决回归问题,进行分类决策,然后使用平均值。具有非常好的可解释性,很明显,不管结果如何,根据流程我们总能说出个123来。
当我们明白了什么是决策树,那么问题来了,要怎么构建决策树呢?换句话说,每个节点要在哪一个维度上面进行划分呢?比如相亲:女性可以从是否有车、有房、长得帅来划分;但是每个维度要在哪一个值上做划分呢?有车有房长得帅,但是房、车、要多好呢?人要多帅呢;以及节点的优先级问题,房、车、长得帅,是先以哪一个节点进行划分呢?这些都是问题,不过目前我们可以通过信息熵的方式进行判断。
2.信息熵
什么是熵?熵在信息论中代表随机变量不确定度的度量。听起来挺深奥的,其实我们在中学的物理化学中就接触了,就是物体的混乱程度。就是物质本质都会沿着熵增大的方向前进。
在机器学习领域,我们也能得到如下结论
熵越大,数据的不确定性越高熵越小,数据的不确定性越低
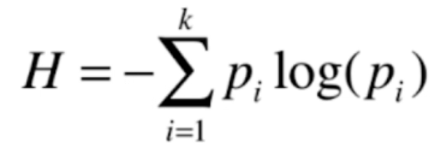
信息熵的计算公式如图所示,其中的k表示,在这个系统中有k个类别,p代表每一个类别所占的比例。前面为什么要加上负号呢?因为p一定是一个小于1的数,那么log(p)显然也是一个小于0的数,因此结果为负数,再加上前面的负号,负负得正了。
我们举个栗子吧
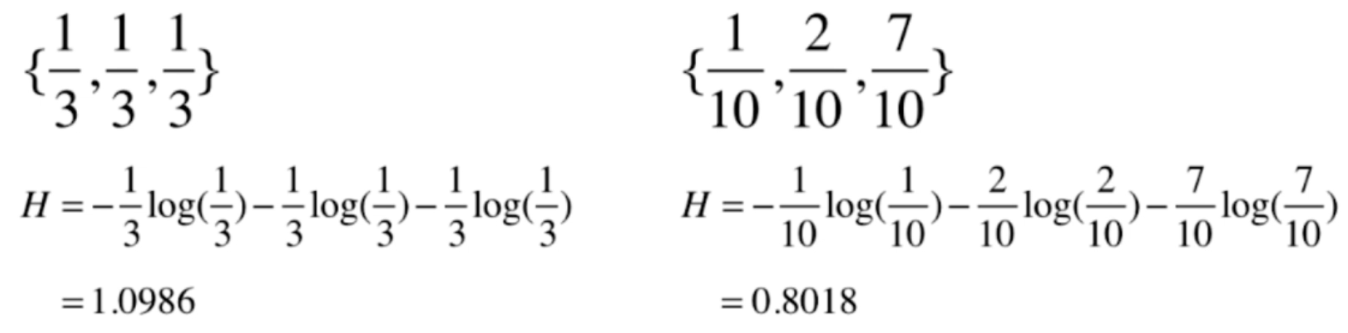
我们看到右边数据的熵是小于左边的,说明右边的数据更稳定。仔细想一下,也能理解,因为右边有百分之70都是同一类数据,右边的数据是更确定的。
栗子再举的极端一点,如果是{1, 0, 0},那么此时的信息熵就是0,这也是信息熵的最低值,说明此时的数据只有一类,没有任何的不确定性。
下面我们就以二分类为例,编程绘制一下图像。首先二分类的话,如果其中一类的比例为x,那么剩余一类一定占1-x,那么信息熵就是H = -xlog(x) - (1 - x)log(1 - x)
import numpy as np
import matplotlib.pyplot as plt
def entropy(p):
return -p * np.log(p) - (1 - p) * np.log(1 - p)
x = np.linspace(0.01, 0.99, 200)
plt.plot(x, entropy(x))
plt.show()

可以看到当二分类的时候,图像整体类似于抛物线的形状,而且当x为0.5的时候,信息熵有最大值,或者此时数据是最不确定的。
那么再回到之前的问题,我们每个节点要在那个维度上进行划分,显然是要沿着信息熵减小的方向上划分。至于在那个值上面做划分,显然是要在熵减小的程度最高的地方划分
3.基尼系数
基尼系数和信息熵本质一样,都是对数据进行划分的一种方式,并且基尼系数还要更简单一些。
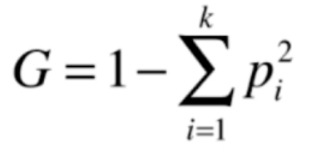
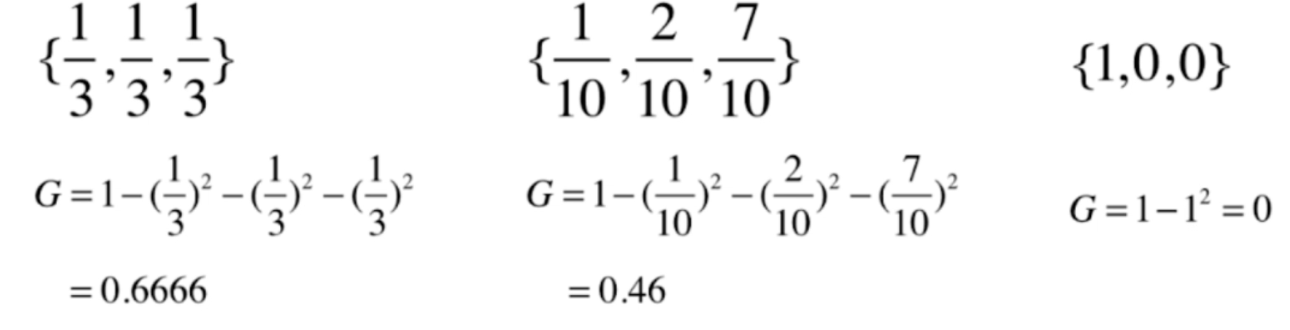
基尼系数和信息熵同样满足相同的规律,值越低,越确定。
下面我们同样以二分类为例,编程绘制一下图像。首先二分类的话,如果其中一类的比例为x,那么剩余一类一定占1-x,那么基尼系数就是G = 1 - x ** 2 - (1 - x) ** 2
import numpy as np
import matplotlib.pyplot as plt
def gini(x):
return 1 - x ** 2 - (1 - x) ** 2
x = np.linspace(0.01, 0.99, 200)
plt.plot(x, gini(x))
plt.show()
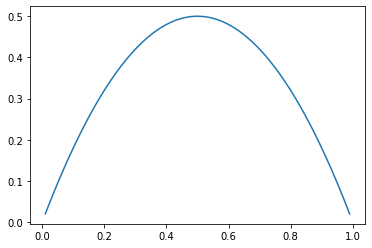
二分类的话,基尼系数和信息熵是一样的。
关于二者具体的区别
熵信息的计算比基尼系数稍慢,在sklearn中,默认使用基尼系数大多数情况下二者没有特别的效果优劣
4.CART与决策树中的超参数
什么是CART,CART(classification and regression tree),使用信息熵和基尼系数构建出来的都是CART树。根据某一个维度d,和阈值v不断地进行二分。那么最终形成的树必定是一个二叉树,sklearn使用的便是CART树,当然除了CART树,还有ID3,C4.5,C5.0等等。
当决策树训练好了之后,那么在进行预测的时候,只需要O(logm)的复杂度,因为每一次都对半查找,但是也显而易见,在训练的时候,复杂度是O(n·m·logm),并且决策树还有一个问题就是和knn一样,容易产生过拟合。实际上非参数学习,都容易产生过拟合,因此我们要进行剪枝,来降低复杂度、解决过拟合。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.tree import DecisionTreeClassifier
# 绘制决策边界
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(1, -1),
np.linspace(axis[3], axis[2], int((axis[3] - axis[2]) * 100)).reshape(1, -1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(["#EF9A9A", "#FFF59D", "#90CAF9"])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
iris = load_iris()
X, y = make_moons(noise=0.25, random_state=666)
# 我们不加任何的参数
dt_clf = DecisionTreeClassifier()
dt_clf.fit(X, y)
plot_decision_boundary(dt_clf, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()
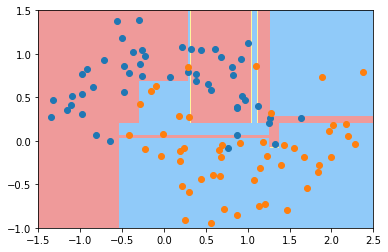
显然当我们不加任何的参数的时候,决策树过拟合了。那么我们就传入一些参数,看看是如何遏制过拟合的。
# 限制深度为2
dt_clf = DecisionTreeClassifier(max_depth=2)
dt_clf.fit(X, y)
plot_decision_boundary(dt_clf, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()
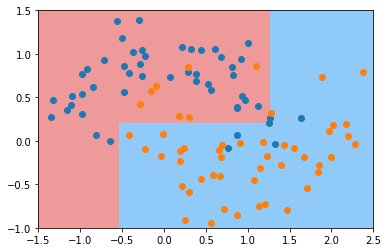
此时就没有过拟合了。我们再来看看其他参数
# 这个参数表示,对于一个节点来说,至少有多少个样本数据,才进行拆分。
dt_clf = DecisionTreeClassifier(min_samples_split=10)
dt_clf.fit(X, y)
plot_decision_boundary(dt_clf, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()
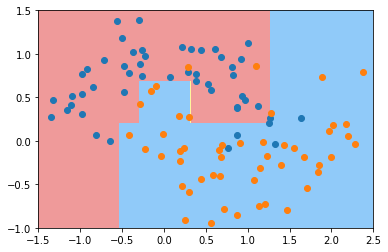
# 这个参数表示,对于一个叶子节点来说,至少要有多少个样本
dt_clf = DecisionTreeClassifier(min_samples_leaf=6)
dt_clf.fit(X, y)
plot_decision_boundary(dt_clf, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()
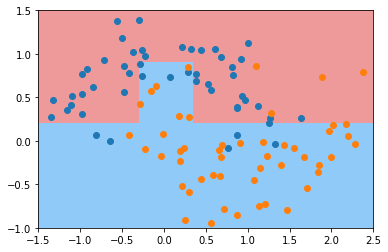
# 这个参数表示,最多有多少个叶子节点
# 叶子节点越多,决策树就越复杂,就越容易产生过拟合。
dt_clf = DecisionTreeClassifier(max_leaf_nodes=4)
dt_clf.fit(X, y)
plot_decision_boundary(dt_clf, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y == 0, 0], X[y == 0, 1])
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.show()
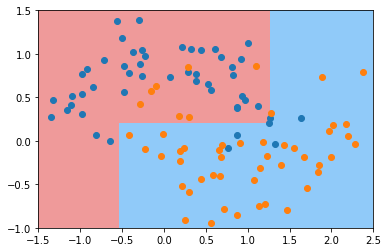
5.决策树解决回归问题
当我们使用决策树解决回归问题时,对于每一个叶子节点都包含了一定的数据。当一个新的数据到来时,走到叶子节点。如果是分类问题,那么就根据当前叶子节点里面的数据进行投票,选择票数多的类别。如果是回归问题,那么就去所有样本数据的平均值。
我们来看看sklearn当中如何解决回归问题。
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
boston = load_boston()
X = boston.data
y = boston.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
dt_reg = DecisionTreeRegressor()
dt_reg.fit(X_train, y_train)
print(dt_reg.score(X_test, y_test)) # 0.6020300890301
# 显然这个结果不尽人意,我们再来看看训练集
print(dt_reg.score(X_train, y_train)) # 1.0
"""
惊奇的是,在训练集上面居然达到了百分之百
毫无疑问,肯定是发生了过拟合。
"""
显然要对决策树进行剪枝,用参数来制约决策树。至于怎么调,可以自己尝试一下。
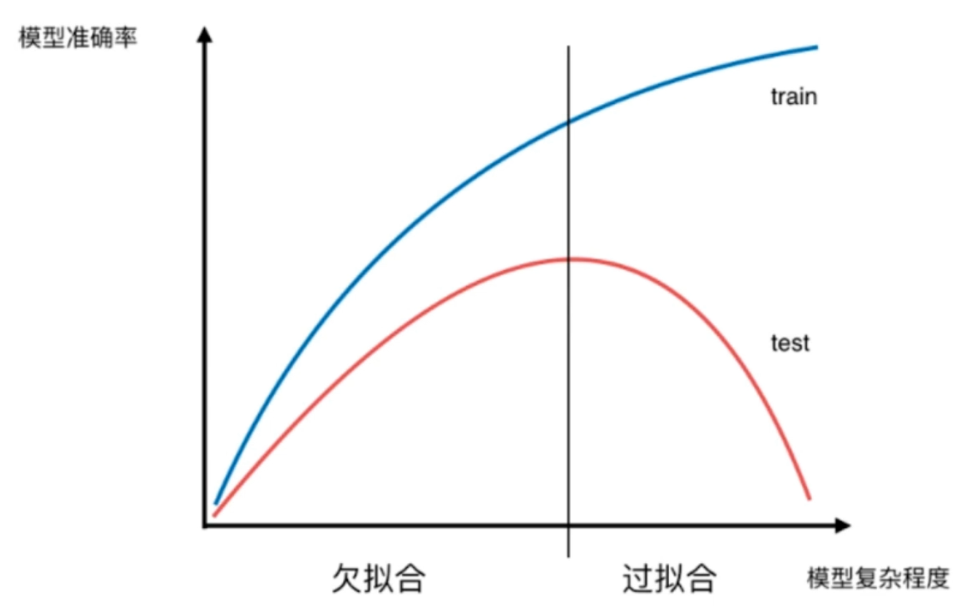
不要忘记这幅图
6.决策树的局限性
回忆一下我们之前使用决策边界来绘制决策树,有没有发现一个特点呢?那就是我们的决策边界都是横平竖直的,这里不难理解,每一次都二分嘛,显然是和坐标轴是平行的。
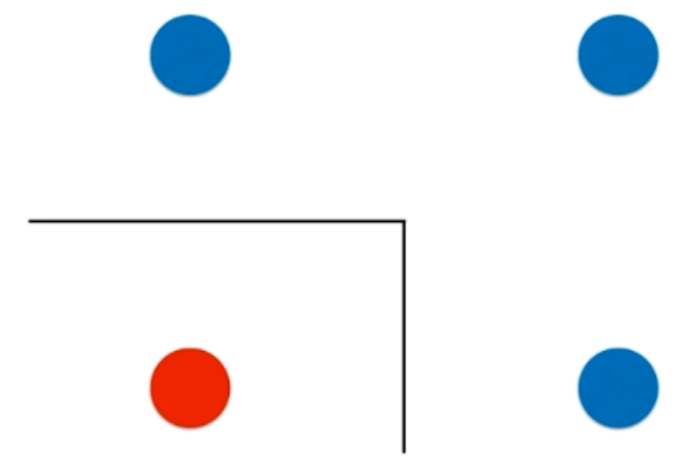
对于图中四个点,如果使用决策树来分的话,显然会横着来一刀,当然竖着来一刀也一样。反正结果都是两个蓝色一组,一红一蓝为一组。首先两个蓝色的显然信息熵已经为0了,然后一红一蓝还需要再切一刀,那么最终变成图中所示的情况。但是这种情况是有局限性的,可能或者这样分会更完美一些。
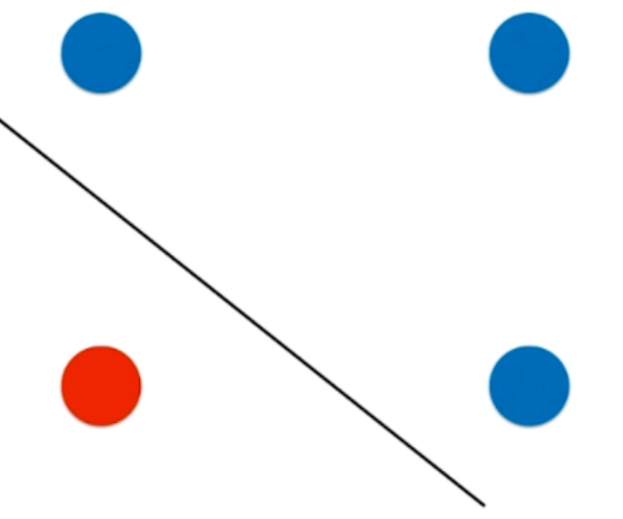
决策边界应该是这样的一根斜线,但是对于决策树来讲的话,决策边界永远不会出现这样的一根斜线。
决策树的另一个局限性就是对个别数据敏感,当然这是所有非参数学习都会有的问题。
因此我们便介绍决策树的两个局限性,但即便如此决策树依旧是一个有用的机器学习算法,它的主要用处并不是单独进行使用,更是用于集成学习。