第一章 语言模型
(自然语言处理课程讲义,Michael Collins,哥伦比亚大学)
1.1 介绍
在这一节,我们将考虑一个问题,即如何为一个例句集建立语言模型。语言模型最初从语音识别发展起来;对现代的语言识别系统,语言模型依然起着中心作用。语言模型在其他自然语言处理应用中也被广泛应用。我们将在本章讨论参数估计技术。参数估计技术最初为语言模型而生,在很多场合都有用,譬如在接下来的章节中将会讨论到的标注问题和句法分析问题。
我们的任务如下。假设我们有一个语料库——某特定语言的句子集。譬如说,我们可能持有泰晤士报数年内的文档,又或者我们可能拥有非常大量的网络文档。基于这些语料,我们希望评估一个语言模型的参数。
语言模型定义如下。首先,我们将该门语言中的所有单词组成的集合定义为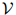 。例如,当我们为英语建立语言模型时,我们可能会有
。例如,当我们为英语建立语言模型时,我们可能会有
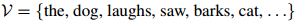
在实际应用中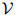 可以是很大的:它可能包含数千甚至数万个单词。我们假设
可以是很大的:它可能包含数千甚至数万个单词。我们假设 是一个有限集。该语言的一个句子就是一个单词序列
是一个有限集。该语言的一个句子就是一个单词序列
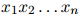
其中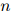 满足
满足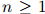 ,且
,且 ,
,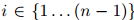 ,且假定
,且假定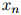 是一个特殊符号——STOP(我们假定STOP并非
是一个特殊符号——STOP(我们假定STOP并非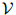 中的元素)。我们将会看到为什么让每个句子以STOP结束是方便的。以下是一些例句:
中的元素)。我们将会看到为什么让每个句子以STOP结束是方便的。以下是一些例句:

我们将定义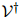 作为取词于
作为取词于 的句子的集合:这是一个无限集,因为句子可以是任意长度的。
的句子的集合:这是一个无限集,因为句子可以是任意长度的。
我们接着给出如下定义:
定义1 (语言模型) 一个语言模型由一个有限集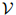 ,以及一个函数
,以及一个函数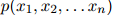 构成,其中
构成,其中 满足:
满足:
1. 对任意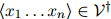 ,
,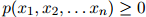
2. 此外,

因此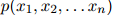 是
是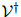 中句子的概率分布。
中句子的概率分布。
对从训练语料库中学习语言模型的一种(非常差劲的)方法,我们考虑如下。将句子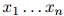 在训练语料库中出现的次数定义为
在训练语料库中出现的次数定义为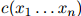 ,训练语料库的句子总数为
,训练语料库的句子总数为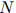 。于是我们可以将
。于是我们可以将 定义为
定义为
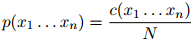
然而,这是一个非常差劲的模型:具体地说,它会将任何未在训练语料库中出现过的句子的概率赋为0。因此它无法遍及那些未在训练语料库中出现过的句子。本章的主要技术贡献就是介绍可以遍及未在训练语料库中出现过的句子的方法。
乍看起来语言模型问题是一个特别奇怪的任务,那么究竟我们为什么要考虑这个问题?有几个理由:
1. 语言模型在非常广泛的应用中都有着重要作用,最明显的或许是语音识别和机器翻译。在很多应用中,获得一个好的先验分布 来描述句子在该种语言中是否可能,是非常有用的。例如,在语音识别中,语言模型与一个语音模型绑定,语音模型是为单词发音而建的模型:想象这种语言模型的一个方法是,语音模型生成大量候选句子,每个句子都附带着一个概率值;语言模型则基于每个句子在该种语言中有是否更有可能是一个句子,来重新分配概率。
来描述句子在该种语言中是否可能,是非常有用的。例如,在语音识别中,语言模型与一个语音模型绑定,语音模型是为单词发音而建的模型:想象这种语言模型的一个方法是,语音模型生成大量候选句子,每个句子都附带着一个概率值;语言模型则基于每个句子在该种语言中有是否更有可能是一个句子,来重新分配概率。
2. 我们所讨论的技术,即用于定义函数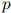 以及用于评估从训练用例中习得的语言模型的参数的技术,将会在课程中提到的其他几个场合下非常有用:例如在我们即将讲到的隐马尔可夫模型中,以及用于语法分析的语言模型中,都非常有用。
以及用于评估从训练用例中习得的语言模型的参数的技术,将会在课程中提到的其他几个场合下非常有用:例如在我们即将讲到的隐马尔可夫模型中,以及用于语法分析的语言模型中,都非常有用。
1.2 马尔可夫模型
现在我们转到一个重要问题:给定一个训练语料库,我们怎样训练出函数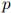 ?在这一节我们讨论概率论中的一个核心概念——马尔可夫模型;在下一节,我们讨论三元语言模型,三元模型是直接建立在马尔可夫模型之上的一类语义模型。
?在这一节我们讨论概率论中的一个核心概念——马尔可夫模型;在下一节,我们讨论三元语言模型,三元模型是直接建立在马尔可夫模型之上的一类语义模型。
1.2.1 针对定长序列的马尔可夫模型
考虑一个随机变量序列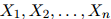 。每一个随机变量值可以取有限集
。每一个随机变量值可以取有限集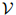 中的任意值。现在我们假设序列的长度
中的任意值。现在我们假设序列的长度 是一个固定的数(例如,
是一个固定的数(例如,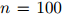 )。在下一节我们将描述怎样将处理方法一般化到
)。在下一节我们将描述怎样将处理方法一般化到 本身也是随机变量的情况,从而允许不同序列拥有不同的长度。
本身也是随机变量的情况,从而允许不同序列拥有不同的长度。
我们的目标如下:我们希望为任何序列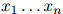 的概率建模,其中
的概率建模,其中 且
且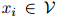 ,
,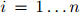 。换言之,就是为如下联合概率建模:
。换言之,就是为如下联合概率建模:
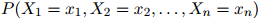
形如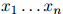 的可能序列有
的可能序列有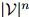 个:所以很明显,对合理的
个:所以很明显,对合理的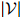 和
和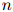 ,罗列所有
,罗列所有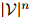 个概率值,并不是一个可行的方法。我们希望建立一个更为强大的模型。
个概率值,并不是一个可行的方法。我们希望建立一个更为强大的模型。
在一阶马尔科夫过程中,我们作如下假设,即将模型简化为:

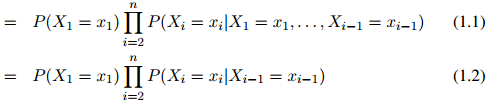
第一步,即公式1.1,是准确的计算方法:根据概率的链式法则,任意分布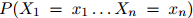 都可以写成这个形式。因此我们在这一步的推演中并没有做出任何假设。然而,第二步,即公式1.2,并不必然是准确的计算方法:我们作出了如下假设,即对任意
都可以写成这个形式。因此我们在这一步的推演中并没有做出任何假设。然而,第二步,即公式1.2,并不必然是准确的计算方法:我们作出了如下假设,即对任意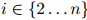 ,任意的
,任意的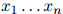 ,有
,有
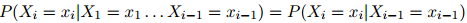
这是其中一个(一阶)马尔可夫假设。我们假设序列中第 个单词的特征仅依赖与它前一个单词,
个单词的特征仅依赖与它前一个单词, 。更规范地说,给定
。更规范地说,给定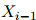 的值,我们假设
的值,我们假设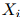 的值条件独立于
的值条件独立于 。
。
在一个二阶马尔可夫过程(二阶马尔可夫过程是建立三元语言模型的基础)中,我们作出一个略微弱一点的假设,即认为序列中的每个单词只依赖于其前两个单词:
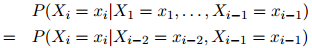
从而整个序列的概率写成
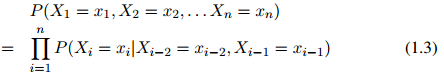
为了方便,在定义中,我们假设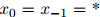 ,其中
,其中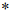 是句子中一个特殊的"星"号。
是句子中一个特殊的"星"号。
1.2.2 针对变长句子的马尔科夫序列
在上一节,我们假设句子的长度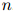 是固定的。然而在很多应用中,
是固定的。然而在很多应用中, 是可变的。因此
是可变的。因此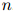 本身也是一个随机变量。为这个长度变量建模的方法有很多:在本节我们讨论一种最为普遍的语言建模方法。
本身也是一个随机变量。为这个长度变量建模的方法有很多:在本节我们讨论一种最为普遍的语言建模方法。
方法是简单的:我们假设序列中第 个单词
个单词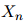 总是等于一个特殊符号——STOP。这个符号只可出现在序列的末尾。我们使用与前面提到的完全相同的假设:例如在二阶马儿可夫假设下,我们有
总是等于一个特殊符号——STOP。这个符号只可出现在序列的末尾。我们使用与前面提到的完全相同的假设:例如在二阶马儿可夫假设下,我们有
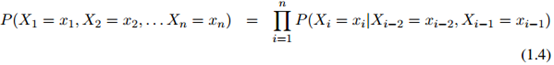
对任意的 和任意
和任意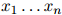 都成立。其中
都成立。其中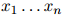 满足
满足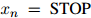 且
且 ,
,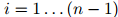 。
。
我们已经假设了一个二阶马尔可夫过程,在这个二阶马尔可夫过程中,我们根据如下分布生成符号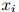 :
:
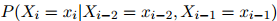
其中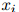 为
为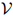 中元素,或者,如果它居于句末的话,是一个STOP符号。如果我们生成了STOP符号,那么我们就已经生成了整个序列。否则,我们接着生成序列中的下一个符号。
中元素,或者,如果它居于句末的话,是一个STOP符号。如果我们生成了STOP符号,那么我们就已经生成了整个序列。否则,我们接着生成序列中的下一个符号。
更规范一点来说,生成句子的过程如下:
1. 初始化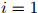 ,
,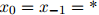
2. 根据如下分布生成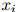 :
:
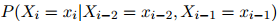
3. 如果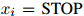 ,返回序列
,返回序列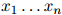 。否则,令
。否则,令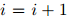 ,并转到第2步。
,并转到第2步。
至此,我们已经拥有了一个能够生成不定长序列的模型。
1.3 三元语言模型
定义语言模型的方式有多种,但在这一章,我们将关注一个特别重要的例子——三元语言模型。这是上一节所提到的马尔可夫模型在语言建模问题上的直接应用。在这一节,我们给出三元模型的基本定义,讨论三元模型的最大似然参数估计,并最后讨论三元模型的优缺点。
1.3.1 基本定义
正如在马尔可夫模型中,我们将每个句子建模为 个随机变量,
个随机变量, 。长度
。长度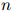 本身也是一个随机变量(对不同的句子可以取不同的值)。我们总有
本身也是一个随机变量(对不同的句子可以取不同的值)。我们总有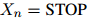 。在一个二阶马尔可夫模型中,每个句子
。在一个二阶马尔可夫模型中,每个句子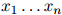 的概率为
的概率为
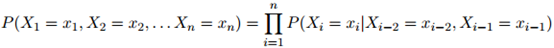
其中,与此前一样,我们假设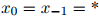 。
。
我们将假设对任意,对任意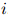 ,对任意
,对任意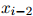 ,
,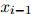 ,
,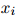 ,
,

其中,对任意 ,
,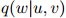 是模型的一个参数。我们将马上看看怎样从训练语料中得到参数
是模型的一个参数。我们将马上看看怎样从训练语料中得到参数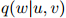 的估计值。于是,对任一序列
的估计值。于是,对任一序列 ,我们的模型是以如下形式呈现的:
,我们的模型是以如下形式呈现的:
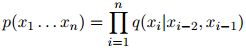
这就引出了以下定义:
定义2(三元语言模型) 一个三元语言模型由一个有限集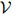 和一个参数
和一个参数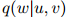 组成。其中
组成。其中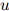 ,
, ,
,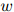 为满足
为满足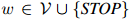 和
和 的任意三元。
的任意三元。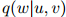 的值可以看作在二元组
的值可以看作在二元组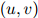 后面出现单词
后面出现单词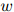 的概率。对任意满足
的概率。对任意满足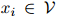 ,
,
 ,且
,且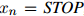 的句子,在该三元语言模型中,该句子的概率为
的句子,在该三元语言模型中,该句子的概率为
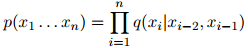
其中,我们定义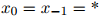 。
。
例如,对句子

我们有
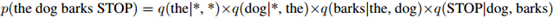
注意到,在这个表达式中,对句子中的每个单词,我们只有一个与之对应的相加项(the,dog,barks,和STOP)。每个单词只依赖于其前两个单词:这就是三元假设。
参数满足如下要求,即对任意三元 ,
, ,
, ,
,
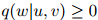
且对任意二元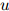 ,
, ,
,
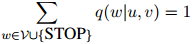
因此,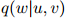 定义了在二元上下文
定义了在二元上下文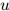 ,
, 的条件下,
的条件下,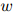 上的一个分布。
上的一个分布。
剩下的主要问题就是如何估计以下所谓的模型的参数:
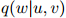
其中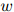 为
为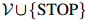 中的任一元素,且
中的任一元素,且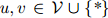 。这个模型共有
。这个模型共有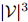 个参数。这看起来是个很大的数字。例如,当
个参数。这看起来是个很大的数字。例如,当 (这是一个符合实际的数字,在现代的标准看来,更像是个很小的数字)时,我们有
(这是一个符合实际的数字,在现代的标准看来,更像是个很小的数字)时,我们有 。
。
1.3.2 最大似然估计
我们从最惯常的解决方法——最大似然估计——开始,讨论参数估计问题。我们将会看到,最大似然估计在一个很重要的方面是存在问题的,但我们将会讨论一些相关的,在实践中效果很好的方法,是怎样从最大似然估计中延伸出来。
首先,约定一些符号。定义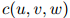 为三元组
为三元组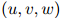 在训练语料中出现的次数:例如,
在训练语料中出现的次数:例如,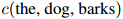 为the dog barks这个由三个单词组成的序列在训练语料中出现的次数。类似地,定义
为the dog barks这个由三个单词组成的序列在训练语料中出现的次数。类似地,定义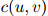 为二元组
为二元组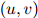 在语料中出现的次数。于是,对任意的
在语料中出现的次数。于是,对任意的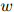 ,
,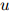 ,
, ,我们定义
,我们定义

作为一个例子,我们对 的估计会是这样的:
的估计会是这样的:
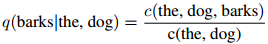
这个估计是非常自然的:分子是整个三元组the dog barks出现的次数,分母则是二元组the dog出现的次数。我们只是简单地求这两个项的比。
不幸地,这种参数估计方法会陷入一个非常严重的主题。回忆一下,我们的模型中包含的参数数量非常庞大(例如,对一个大小为10,000的词典,我们有大约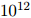 个参数)。出于这个原因,我们的很多计数将会是零。这会引致两个问题:
个参数)。出于这个原因,我们的很多计数将会是零。这会引致两个问题:
- 由于分子计数为0,在上述估计中,将会出现很多
 的情况。这将导致很多三元组的概率未被估算:模型的参数数量远多于训练语料库中单词的数量,因此将任何未在训练语料库中出现过的三元组的概率赋为0,似乎都是不合理的。
的情况。这将导致很多三元组的概率未被估算:模型的参数数量远多于训练语料库中单词的数量,因此将任何未在训练语料库中出现过的三元组的概率赋为0,似乎都是不合理的。
- 对分母
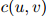 等于零的情况,这种估算没有给出妥善的定义。
等于零的情况,这种估算没有给出妥善的定义。
我们将简短地看看怎样构思一些经过修改的估算方法来修复这些问题。然而,在此之前,我们首先讨论怎样对语言模型进行评价,并讨论一下三元语言模型的优缺点。
1.3.3 评价语言模型:迷惑度
那么,我们怎样度量一个语言模型的质量呢?一个非常惯用的方法,是评价模型在特别划分出来的数据上的迷惑度。
方法如下。假设我们有一些测试数据,即测试句子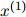 ,
,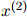 ,…,
,…,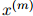 。每一个测试句子
。每一个测试句子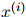 (
(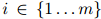 )是单词序列
)是单词序列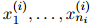 ,其中
,其中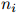 是第
是第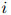 个句子的长度。与以往一样,我们假设每个句子以符号STOP结束。
个句子的长度。与以往一样,我们假设每个句子以符号STOP结束。
很重要的一点是,这些测试句子都是特别划分出来的,他们并非用来估计模型的时候所用的语料的任何一个部分。在这个意义上来说,他们是一些没有见到过的新的句例。
对任一测试句子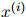 ,我们可以度量它在语言模型中的概率
,我们可以度量它在语言模型中的概率 。一个自然的,用来度量语言模型质量的方法,是计算整个测试句子集的概率和,也就是
。一个自然的,用来度量语言模型质量的方法,是计算整个测试句子集的概率和,也就是
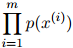
这样做,基于如下直观理由:模型在这方面的质量越高,则模型对未出现过的句子的建模就越好。
在测试语料上的迷惑度,就是派生于这种质量的一个直接转换。定义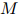 为测试语料中单词的总数。更准确地说,在
为测试语料中单词的总数。更准确地说,在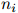 是第
是第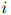 个句子的长度这个定义之下,
个句子的长度这个定义之下,
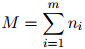
那么,在该模型下的平均对数概率(log probability)定义为
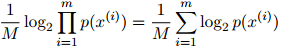
这其实就是整个测试语料库的对数概率,除以语料库中单词的总数。这里我们用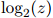 来表示以2为底的
来表示以2为底的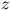 的对数,其中
的对数,其中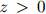 。同样地,模型在这方面的质量越高,则模型越好。
。同样地,模型在这方面的质量越高,则模型越好。
于是,迷惑度定义为
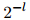
其中
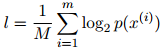
因此,我们是对平均对数概率取负值,并将其作为2的指数,来得到迷惑度的计算公式的。(再次说明,这一节中,我们假设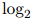 是以2为底的对数)。迷惑度是一个正数。迷惑度的值越小,则模型对未出现过的句子的建模就越好。
是以2为底的对数)。迷惑度是一个正数。迷惑度的值越小,则模型对未出现过的句子的建模就越好。
迷惑度背后的一些直观理由如下。譬如说我们有一个词典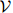 ,其中
,其中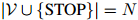 ,且对所有的
,且对所有的 ,
, ,
,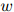 ,模型作出了如下估算
,模型作出了如下估算
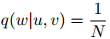
可以看到这是一个笨拙的模型,他将模型简单地估算为在词典以及符号STOP之上的一个平均分布。在这个例子中,可以算得模型的迷惑度等于 。因此,在一个平均分布的概率模型中,迷惑度就等于词典的大小。迷惑度可以被看作是在特定模型下的有效词典大小:例如,如果模型的迷惑度为120(尽管词典的真实大小是,譬如说10,000),那么这个词典就粗略地相当于一个有效大小为120的词典。
。因此,在一个平均分布的概率模型中,迷惑度就等于词典的大小。迷惑度可以被看作是在特定模型下的有效词典大小:例如,如果模型的迷惑度为120(尽管词典的真实大小是,譬如说10,000),那么这个词典就粗略地相当于一个有效大小为120的词典。
为了给出更多动因,相对简单地说,迷惑度等于

其中

这里我们用 来表示
来表示 的
的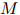 次方根:所以
次方根:所以 就是满足
就是满足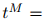
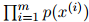 的
的 。给定
。给定
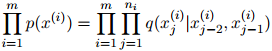
且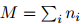 ,
, 就是
就是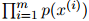 中的项
中的项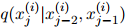 的几何平均数(geometric mean)。例如,如果迷惑度等于100,那么
的几何平均数(geometric mean)。例如,如果迷惑度等于100,那么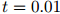 ,表示几何平均数为0.01。
,表示几何平均数为0.01。
再一个与迷惑度有关的有用的事实如下。如果对在测试数据中出现的任意三元 ,
, ,
,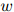 ,我们有估计
,我们有估计
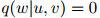
那么迷惑度将会是 。为了看清这一点,只需注意到,在这种情况下,测试语料库在模型下的概率将会为0,从而平均对数概率将会是
。为了看清这一点,只需注意到,在这种情况下,测试语料库在模型下的概率将会为0,从而平均对数概率将会是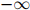 。因此如果我们真的要以迷惑度作为一个语言模型的度量,那么我们应该不惜一切避免0估算值的出现。
。因此如果我们真的要以迷惑度作为一个语言模型的度量,那么我们应该不惜一切避免0估算值的出现。
最后,讲讲迷惑度一些"典型"取值背后的理由。Goodman("A bit of progress in language modeling",图2)在词典大小为50,000的英语数据上,评价了一元、二元,以及三元语言模型。在一个二元模型中,我们的参数形式为 ,且有
,且有

故此每个单词仅依赖于它在句子中的前一个单词。在一个一元模型中,我们有参数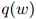 ,且有
,且有
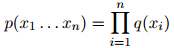
故此每个单词完全独立与句子中其他单词。在Goodman的报告中,三元模型的迷惑度为74,二元模型为137,而一元模型则为955。简单地给词典中每个词赋概率值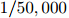 的模型,其迷惑度为50,000。因此,对比二元模型和一元模型,三元模型明显地取得了一个大提升,而对比简单地给词典中每个词赋概率值
的模型,其迷惑度为50,000。因此,对比二元模型和一元模型,三元模型明显地取得了一个大提升,而对比简单地给词典中每个词赋概率值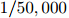 的做法,三元模型取得了巨大的提升。
的做法,三元模型取得了巨大的提升。
1.3.4 三元模型的优缺点
三元模型无可厚非是很强的,且在语言学上是天真单纯的(相关讨论请参阅课程的幻灯片)。然而,它在实践中却延伸出一些非常有用的模型。
1.4 三元模型的平滑估算
如前所述,一个三元语言模型包含非常大量的参数。最大似然参数估计,形式如
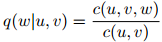
在稀疏数据中会出现严重问题。即便对一个大的训练数据集,很多频次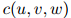 或
或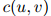 将会是低的,甚至会等于0。
将会是低的,甚至会等于0。
在这一节,我们讨论平滑估算方法,这些方法能够缓和在稀疏数据中会出现的问题。主要思想是依靠更低阶的统计估计——特别地,是基于二元或一元计数的估计——去"平滑"基于三元的估计。我们讨论两种在实践中被非常普遍地使用的平滑方法:首先,是线性插值法;其次,是折扣方法。
1.4.1 线性插值
线性插值的三元模型如下派生。我们定义三元、二元,以及一元最大似然估计如下:
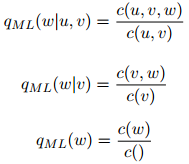
其中,我们扩展了我们的符号: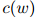 是
是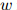 在训练语料库中出现的次数,
在训练语料库中出现的次数,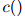 是训练语料库中出现的单词的总数。
是训练语料库中出现的单词的总数。
三元、二元,以及一元估计具有不同的优缺点。一元估计永远不会出现分子或分母等于0的问题;因此这种估计永远是已经定义完善了的,且总是大于0(假如每个单词在训练语料库中出现至少一次;这是一个合理的假设)。然而,一元估计完全忽视上下文(前两个单词),因此漏掉了非常有价值的信息。相比之下,三元估计确实利用了上下文信息,但存在大量的频次计数等于0的问题。二元估计则介于这两种情况之间。
线性插值的思想,就是同时使用这三种估计,将三元估计定义如下:

这里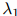 ,
, ,以及
,以及 是模型中三个额外的参数,满足
是模型中三个额外的参数,满足
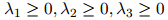
且
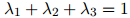
因此我们是取了三种估计的一个加权平均。
有不同的方法估计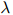 的值。一个惯用的方法如下。譬如说我们有一些额外划分出来的数据,这些数据是从训练语料库以及测试语料库之外划分出来的。我们称这些数据为开发数据(development data)。定义
的值。一个惯用的方法如下。譬如说我们有一些额外划分出来的数据,这些数据是从训练语料库以及测试语料库之外划分出来的。我们称这些数据为开发数据(development data)。定义 为三元组
为三元组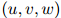 在开发数据中出现的次数。容易看到开发数据的对数似然估计(log-likelihood),是包含参数
在开发数据中出现的次数。容易看到开发数据的对数似然估计(log-likelihood),是包含参数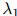 ,
,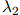 ,
, 的函数
的函数
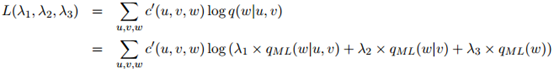
我们倾向于选择使得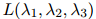 尽量大的
尽量大的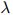 值。
值。
因此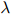 的值取为
的值取为
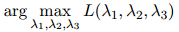
并满足
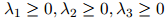
和

寻找 ,
,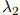 ,
,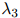 的最优解是非常直接的(参见第??节中的一个算法,该算法常用作此目的)。
的最优解是非常直接的(参见第??节中的一个算法,该算法常用作此目的)。
如前描述,我们的方法有三个平滑参数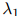 ,
,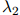 ,和
,和 。三个参数可以理解成分别置于三元、二元,以及一元估计之上的可信度或权重。例如,如果
。三个参数可以理解成分别置于三元、二元,以及一元估计之上的可信度或权重。例如,如果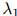 接近于1,意味着我们在三元估计
接近于1,意味着我们在三元估计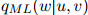 上放置了一个重要的权重;反过来说,如果接近于0,代表我们在三元估计上放置了一个低权重。
上放置了一个重要的权重;反过来说,如果接近于0,代表我们在三元估计上放置了一个低权重。
在实践中,增加一个额外的自由度是重要的,使得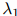 ,
,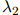 ,和
,和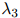 根据作为条件的二元组
根据作为条件的二元组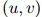 的不同,可以取不同的值。特别地,该方法可以拓展到当
的不同,可以取不同的值。特别地,该方法可以拓展到当 更大的时候,允许
更大的时候,允许 取更大的值——这样做的理由是,一个更大的
取更大的值——这样做的理由是,一个更大的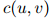 值,应该使我们更为相信三元估计在其中所起的作用。
值,应该使我们更为相信三元估计在其中所起的作用。
至少,这个方法可以用来确保当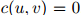 时,
时,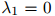 ,因为在这种情况下三元估计
,因为在这种情况下三元估计

是未被定义的。类似地,如果 和
和 都等于零,我们需要令
都等于零,我们需要令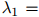
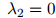 ,因为二元和三元ML估计都是未被定义的。
,因为二元和三元ML估计都是未被定义的。
该方法的一个延伸,通常称之为分桶法(bucketing),将在1.5.1节进行讨论。此外,一个更为简单的方法,如下定义
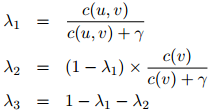
其中 是该方法中唯一的参数。可以看到,
是该方法中唯一的参数。可以看到,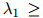
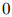 ,
, ,且
,且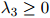 ,并且同样地,
,并且同样地,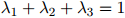 。
。
在这个定义下,可以看到,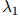 随着
随着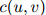 增大而增大,类似地,
增大而增大,类似地,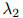 随着
随着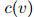 增大而增大。此外,我们可以得知,当
增大而增大。此外,我们可以得知,当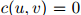 时,
时,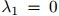 ,当
,当 时,
时,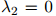 。
。 同样取使得开发数据的对数似然估计最大化的值。
同样取使得开发数据的对数似然估计最大化的值。
这种方法是相对粗糙的,而且并不像是可以取得最优解的方法。然而,这种方法很简单,在某些实际应用中,表现不俗。
1.4.2 折扣方法
我们现在讨论另一种估计方法,这种方法同样在实践中得到普遍应用。首先考虑,对一个用于估计三元模型的方法,我们的目标是定义
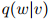
满足任意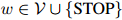 ,
,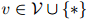 。
。
第一步将会是定义折扣计数(discounted counts)。对任一满足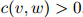 的二元组
的二元组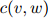 ,我们定义它的折扣计数为
,我们定义它的折扣计数为
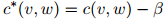
其中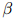 是介乎0和1之间的值(一个典型的取值是
是介乎0和1之间的值(一个典型的取值是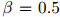 )。因此我们的做法只是简单地从计数中减掉一个常数
)。因此我们的做法只是简单地从计数中减掉一个常数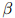 。这样做的理由是,如果我们只从训练语料库中取得计数,我们将全面地高估语料库中所出现的二元组的概率(并且低估了未在语料库中出现的二元组的概率)。
。这样做的理由是,如果我们只从训练语料库中取得计数,我们将全面地高估语料库中所出现的二元组的概率(并且低估了未在语料库中出现的二元组的概率)。
对任一满足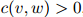 的二元组
的二元组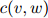 ,我们接着定义
,我们接着定义
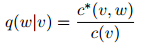
因此在这个表达式中,我们是用折扣后的计数来作为分子,而分母则用的是常规的计数。
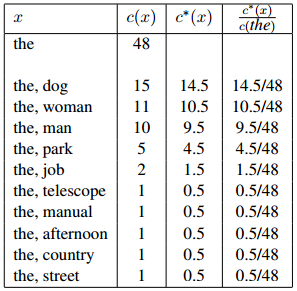
图1.1:用于说明折扣方法的一个例子。我们展示的是一个刻意构造的例子,其中一元the出现48次,我们列出了所有满足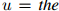 且
且 的二元组
的二元组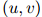 (这些二元计数的总和为48)。此外我们展示了折扣计数
(这些二元计数的总和为48)。此外我们展示了折扣计数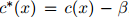 ,其中
,其中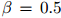 ,且最后我们展示了基于折扣计数的估计
,且最后我们展示了基于折扣计数的估计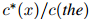 。
。
对任意上下文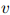 ,这个定义会导致一些丢失概率权重(missing probability mass)的存在,这些丢失概率权重定义为
,这个定义会导致一些丢失概率权重(missing probability mass)的存在,这些丢失概率权重定义为
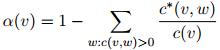
作为一个例子,考虑图1.1所示例子中的计数。在这个例子中我们展示了所有满足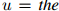 且
且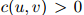 的二元组
的二元组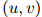 。我们使用的折扣值为
。我们使用的折扣值为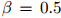 。在这个例子中我们有
。在这个例子中我们有
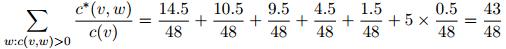
并且有丢失权重
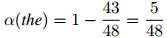
折扣法背后的动机是,除以满足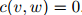 的单词
的单词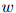 间的这个丢失权重。
间的这个丢失权重。
更具体地,该估计的完整定义如下。对任意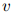 ,定义集合
,定义集合
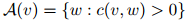
以及

举例来说,对图1.1中的数据,我们会有
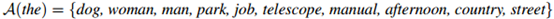
而 则是剩余单词的集合。
则是剩余单词的集合。
于是定义估计为
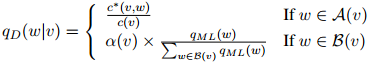
因此做法是,如果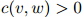 ,我们返回估计
,我们返回估计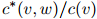 ;否则,我们以一元估计
;否则,我们以一元估计 占所有一元估计的比例返回剩余的概率权重
占所有一元估计的比例返回剩余的概率权重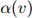 。
。
这个方法可以以一种自然的,递归的方法一般化到三元模型当中:对任意二元组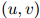 ,定义
,定义
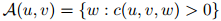
以及

定义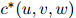 为三元组
为三元组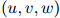 折扣后的计数:也就是,
折扣后的计数:也就是,
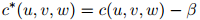
其中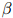 同样地,是折扣值。于是三元模型就是
同样地,是折扣值。于是三元模型就是
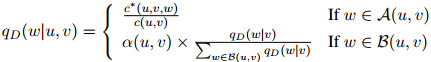
其中
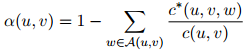
同样地,是所谓"丢失"的概率权重。注意到我们以二元估计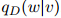 所占的比例来返回这个丢失概率权重,而
所占的比例来返回这个丢失概率权重,而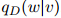 就是我们前面定义的二元估计。
就是我们前面定义的二元估计。
这个方法的唯一一个参数就是折扣值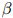 。与线性插值模型一样,选取这个折扣值的惯常方法,是取使得开发语料库的似然估计最大化的折扣值,这里所说的开发语料库,同样是在训练语料库以及测试语料库以外所划分出来数据。定义
。与线性插值模型一样,选取这个折扣值的惯常方法,是取使得开发语料库的似然估计最大化的折扣值,这里所说的开发语料库,同样是在训练语料库以及测试语料库以外所划分出来数据。定义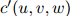 为三元
为三元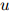 ,
, ,
,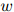 在开发语料库中出现的次数。开发数据的对数似然为
在开发语料库中出现的次数。开发数据的对数似然为

其中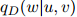 如前面所定义。估计
如前面所定义。估计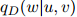 的参数会根据
的参数会根据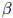 的不同而不同。通常我们会对一个可能
的不同而不同。通常我们会对一个可能 值集进行测试——例如,我们可能会测试集合
值集进行测试——例如,我们可能会测试集合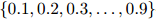 中的所有值——对其中的每个
中的所有值——对其中的每个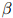 ,我们计算它在开发数据上的对数似然。然后我们选取最大化这个对数似然的值作为
,我们计算它在开发数据上的对数似然。然后我们选取最大化这个对数似然的值作为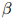 值。
值。
1.5 高级主题
1.5.1 带分桶的线性插入法
在线性插入模型中,待估参数定义为
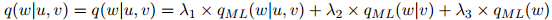
其中 ,
,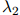 ,和
,和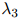 是该方法中的平滑参数。
是该方法中的平滑参数。
在实践中,允许平滑参数随着作为条件的二元组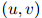 的不同而不同,是重要的——特别地,计数
的不同而不同,是重要的——特别地,计数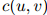 越高,则
越高,则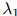 的权重应该越高(类似地,计数
的权重应该越高(类似地,计数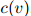 越高,则
越高,则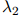 的权重应该越高)。达到这个目的的经典方法是一个拓展后的方法,这个方法被称为分桶法。
的权重应该越高)。达到这个目的的经典方法是一个拓展后的方法,这个方法被称为分桶法。
这种方法的第一步是定义一个函数 令二元
令二元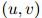 与值
与值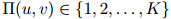 对应起来,其中
对应起来,其中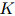 是整数,表示桶的数量。函数是人工定义的,且通常取决于在训练语料中得到的计数。其中一种(这里
是整数,表示桶的数量。函数是人工定义的,且通常取决于在训练语料中得到的计数。其中一种(这里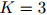 )定义是
)定义是
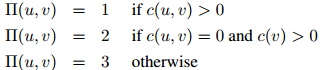
这是一个非常简单的定义,仅仅检测了计数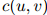 和
和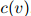 是否等于0。
是否等于0。
另一个略微复杂一点的定义(这个定义对二元组的频率更为敏感)是
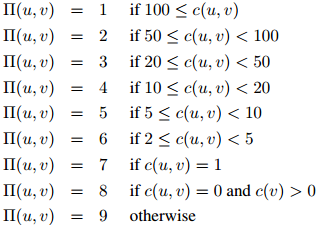
给定函数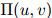 的一个定义,我们接着介绍对应与所有
的一个定义,我们接着介绍对应与所有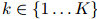 的平滑参数
的平滑参数 ,
,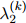 ,
,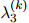 。因此,每一个桶都拥有它自己的平滑参数集。对所有
。因此,每一个桶都拥有它自己的平滑参数集。对所有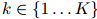 ,我们有限制
,我们有限制
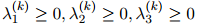
和
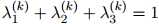
线性插值估计将会是
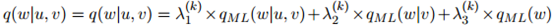
其中
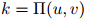
故此,我们已经粗略地介绍了(建立在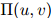 值之上的)平滑参数的一个依托物。因此每一个二元组都有自己的平滑参数;平滑参数的值随
值之上的)平滑参数的一个依托物。因此每一个二元组都有自己的平滑参数;平滑参数的值随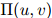 值(
值( 值通常直接与计数
值通常直接与计数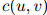 和
和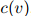 相关)的不同而不同。
相关)的不同而不同。
平滑参数同样使用开发数据集进行估计。如果我们同样地定义 为三元
为三元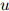 ,
, ,
,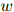 在开发数据中出现的次数,则开发数据的对数似然为
在开发数据中出现的次数,则开发数据的对数似然为
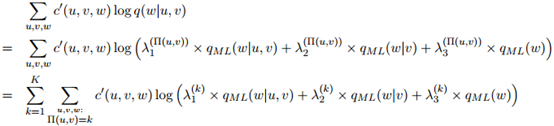
参数 ,
,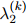 ,
,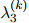 则取最大化这个似然函数的值。
则取最大化这个似然函数的值。
英版原文:http://www.cs.columbia.edu/~mcollins/lm-spring2013.pdf
课程主页:http://www.cs.columbia.edu/~cs4705/
Michael Collins的个人主页:http://www.cs.columbia.edu/~mcollins/
 的情况。这将导致很多三元组的概率未被估算:模型的参数数量远多于训练语料库中单词的数量,因此将任何未在训练语料库中出现过的三元组的概率赋为0,似乎都是不合理的。
的情况。这将导致很多三元组的概率未被估算:模型的参数数量远多于训练语料库中单词的数量,因此将任何未在训练语料库中出现过的三元组的概率赋为0,似乎都是不合理的。
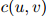 等于零的情况,这种估算没有给出妥善的定义。
等于零的情况,这种估算没有给出妥善的定义。