相关系数度量指的是两个不同事件彼此之间的相互影响程度;而自相关系数度量的是同一事件在两个不同时期之间的相关程度,形象的讲就是度量自己过去的行为对自己现在的影响。
自相关,也称 序列相关。是一个信号于其自身在不同时间点的互相关。非正式地来说,它就是两次观察之间的相似度对它们之间的时间差的函数。它是找出重复模式(如被噪声掩盖的周期信号),或识别隐含在信号谐波频率中消失的基频的数学工具。它常用于信号处理中,用来分析函数或一系列值,如时域信号。
皮尔森相关:
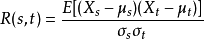
由于在自相关时,x的期望和方差不随着时间的变化而改变。则自相关函数可以表示为时间延迟 ![]() 的函数,如下:
的函数,如下:
主要性质如下:
(1)自相关函数为偶函数,其图形对称于纵轴。
(2)当s=t 时,自相关函数具有最大值,且等于信号的均方值,即
(3)周期信号的自相关函数仍为同频率的周期信号。
意义:
两个相关函数都是对相关性,即相似性的度量。如果进行归一化,会看的更清楚。
自相关就是函数和函数本身的相关性,当函数中有周期性分量的时候,自相关函数的极大值能够很好的体现这种周期性。互相关就是两个函数之间的相似性,当两个函数都具有相同周期分量的时候,它的极大值同样能体现这种周期性的分量。
相关运算从线性空间的角度看其实是内积运算,而两个向量的内积在线性空间中表示一个向量向另一个向量的投影,表示两个向量的相似程度,所以相关运算就体现了这种相似程度。
R语言计算相关系数,首先需要加载cor()函数包,它可以计算三种不同的相关系数如Pearson相关系数、Spearman相关系数、Kendall相关系数。而pcor()函数包则是计算偏相关系数。
acf(c2) #自相关图
> pacf(c2) #偏自相关图
相关系数可视化:https://blog.csdn.net/flyfrommath/article/details/76777412
参考:https://blog.csdn.net/dengheCSDN/article/details/78848046
偏相关分析是指当两个变量同时与第三个变量相关时,将第三个变量的影响剔除,只分析另外两个变量之间相关程度的过程,判定指标是相关系数的R值。
某一个要素对另一个要素的影响或相关程度时,把其他要素的影响视为常数,即暂不考虑其他要素的影响,而单独研究那两个要素之间的 相互关系的密切程度时,称为偏相关。
在排除了其他变量的影响情况下再计算两变量的(简单)相关系数