吴裕雄 数据挖掘与分析案例实战（6）——线性回归预测模型

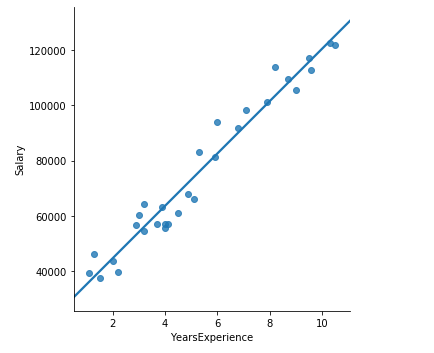
# 工作年限与收入之间的散点图
# 导入第三方模块
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# 导入数据集
income = pd.read_csv(r'F:\python_Data_analysis_and_mining\07\Salary_Data.csv')
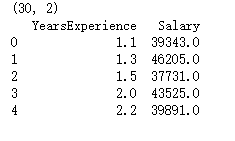
print(income.shape)
print(income.head())
# 绘制散点图
sns.lmplot(x = 'YearsExperience', y = 'Salary', data = income, ci = None)
# 显示图形
plt.show()

# 简单线性回归模型的参数求解
# 样本量
n = income.shape[0]
# 计算自变量、因变量、自变量平方、自变量与因变量乘积的和
sum_x = income.YearsExperience.sum()
sum_y = income.Salary.sum()
sum_x2 = income.YearsExperience.pow(2).sum()
xy = income.YearsExperience * income.Salary
sum_xy = xy.sum()
# 根据公式计算回归模型的参数
b = (sum_xy-sum_x*sum_y/n)/(sum_x2-sum_x**2/n)
a = income.Salary.mean()-b*income.YearsExperience.mean()
# 打印出计算结果
print('回归参数a的值：',a)
print('回归参数b的值：',b)

# 导入第三方模块
import statsmodels.api as sm

# 利用收入数据集，构建回归模型
fit = sm.formula.ols('Salary ~ YearsExperience', data = income).fit()
# 返回模型的参数值
print(fit.params)

# 多元线性回归模型的构建和预测
# 导入模块
from sklearn import model_selection

# 导入数据
Profit = pd.read_excel(r'F:\python_Data_analysis_and_mining\07\Predict to Profit.xlsx')
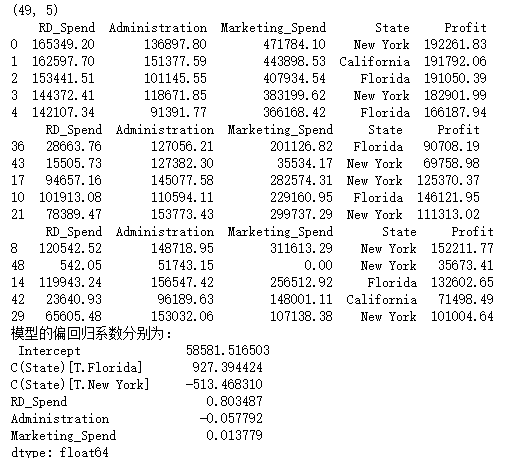
print(Profit.shape)
print(Profit.head())
# 将数据集拆分为训练集和测试集
train, test = model_selection.train_test_split(Profit, test_size = 0.2, random_state=1234)
print(train.head())
print(test.head())
# 根据train数据集建模
model = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend + C(State)', data = train).fit()
print('模型的偏回归系数分别为： ', model.params)
# 删除test数据集中的Profit变量，用剩下的自变量进行预测
test_X = test.drop(labels = 'Profit', axis = 1)
pred = model.predict(exog = test_X)
print('对比预测值和实际值的差异： ',pd.DataFrame({'Prediction':pred,'Real':test.Profit}))

# 生成由State变量衍生的哑变量
dummies = pd.get_dummies(Profit.State)
# 将哑变量与原始数据集水平合并
Profit_New = pd.concat([Profit,dummies], axis = 1)
print(Profit_New.shape)
print(Profit_New.head())
# 删除State变量和California变量（因为State变量已被分解为哑变量，New York变量需要作为参照组）
Profit_New.drop(labels = ['State','New York'], axis = 1, inplace = True)

# 拆分数据集Profit_New
train, test = model_selection.train_test_split(Profit_New, test_size = 0.2, random_state=1234)
# 建模
model2 = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend + Florida + California', data = train).fit()
print('模型的偏回归系数分别为： ', model2.params)

# 导入第三方模块
import numpy as np

# 计算建模数据中，因变量的均值
ybar = train.Profit.mean()
print(ybar)
# 统计变量个数和观测个数
p = model2.df_model
print(p)
n = train.shape[0]
print(n)
# 计算回归离差平方和
RSS = np.sum((model2.fittedvalues-ybar) ** 2)
print(RSS)
# 计算误差平方和
ESS = np.sum(model2.resid ** 2)
print(ESS)
# 计算F统计量的值
F = (RSS/p)/(ESS/(n-p-1))
print('F统计量的值：',F)
# 返回模型中的F值
print(model2.fvalue)

# 导入模块
from scipy.stats import f

# 计算F分布的理论值
F_Theroy = f.ppf(q=0.95, dfn = p,dfd = n-p-1)
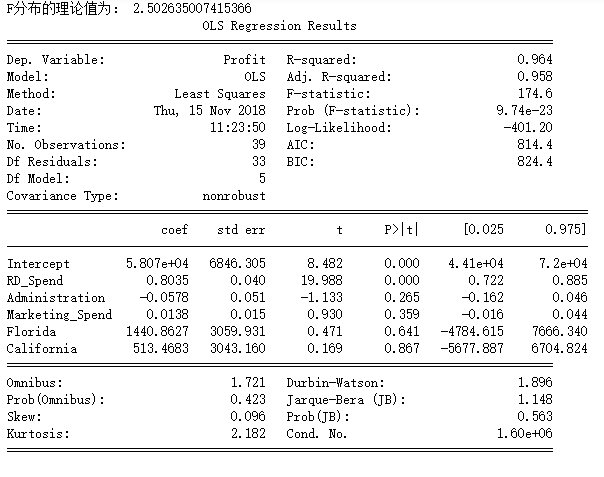
print('F分布的理论值为：',F_Theroy)

# 模型的概览信息
print(model2.summary())

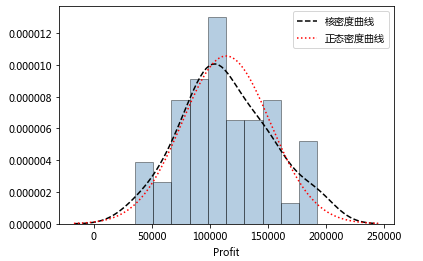
# 正态性检验
# 直方图法
# 导入第三方模块
import scipy.stats as stats

# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 绘制直方图
sns.distplot(a = Profit_New.Profit, bins = 10, fit = stats.norm, norm_hist = True,
hist_kws = {'color':'steelblue', 'edgecolor':'black'},
kde_kws = {'color':'black', 'linestyle':'--', 'label':'核密度曲线'},
fit_kws = {'color':'red', 'linestyle':':', 'label':'正态密度曲线'})
# 显示图例
plt.legend()
# 显示图形
plt.show()

# 残差的正态性检验（PP图和QQ图法）
pp_qq_plot = sm.ProbPlot(Profit_New.Profit)
# 绘制PP图
pp_qq_plot.ppplot(line = '45')
plt.title('P-P图')
# 绘制QQ图
pp_qq_plot.qqplot(line = 'q')
plt.title('Q-Q图')
# 显示图形
plt.show()

# 导入模块
import scipy.stats as stats

a = stats.shapiro(Profit_New.Profit)
print(a)
# 生成正态分布和均匀分布随机数
rnorm = np.random.normal(loc = 5, scale=2, size = 10000)
print(rnorm)
runif = np.random.uniform(low = 1, high = 100, size = 10000)
print(runif)
# 正态性检验
KS_Test1 = stats.kstest(rvs = rnorm, args = (rnorm.mean(), rnorm.std()), cdf = 'norm')
print(KS_Test1)
KS_Test2 = stats.kstest(rvs = runif, args = (runif.mean(), runif.std()), cdf = 'norm')
print(KS_Test2)

# 导入statsmodels模块中的函数
from statsmodels.stats.outliers_influence import variance_inflation_factor

# 自变量X(包含RD_Spend、Marketing_Spend和常数列1)
X = sm.add_constant(Profit_New.ix[:,['RD_Spend','Marketing_Spend']])
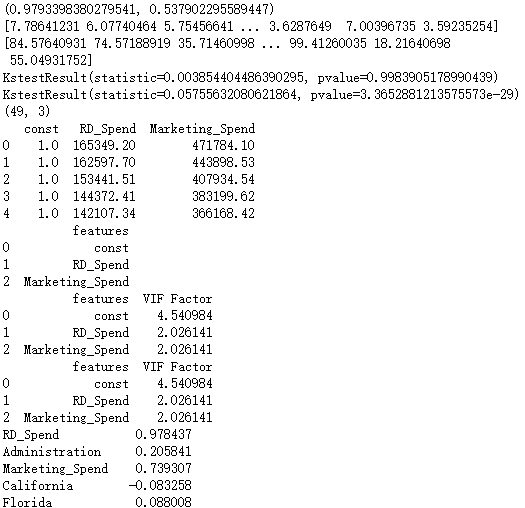
print(X.shape)
print(X.head())

# 构造空的数据框，用于存储VIF值
vif = pd.DataFrame()
vif["features"] = X.columns
print(vif)
vif["VIF Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
print(vif)
# 返回VIF值
print(vif)

# 计算数据集Profit_New中每个自变量与因变量利润之间的相关系数
a = Profit_New.drop('Profit', axis = 1).corrwith(Profit_New.Profit)
print(a)

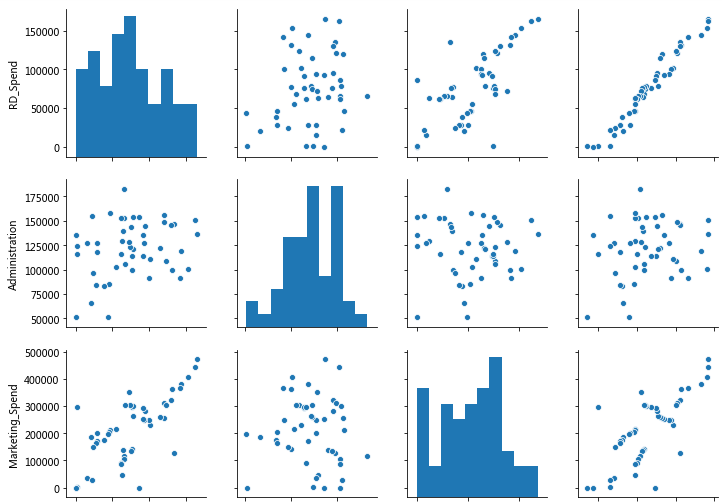
# 散点图矩阵
# 导入模块
import matplotlib.pyplot as plt
import seaborn

# 绘制散点图矩阵
seaborn.pairplot(Profit_New.ix[:,['RD_Spend','Administration','Marketing_Spend','Profit']])
# 显示图形
plt.show()

import statsmodels.formula.api as smf

# 模型修正
model3 = smf.ols('Profit ~ RD_Spend + Marketing_Spend', data = train).fit()
# 模型回归系数的估计值
print(model3.params)
# 异常值检验
outliers = model3.get_influence()
print(outliers)
# 高杠杆值点（帽子矩阵）
leverage = outliers.hat_matrix_diag
print(leverage)
# dffits值
dffits = outliers.dffits[0]
print(dffits)
# 学生化残差
resid_stu = outliers.resid_studentized_external
print(resid_stu)
# cook距离
cook = outliers.cooks_distance[0]
print(cook)
# 合并各种异常值检验的统计量值
contat1 = pd.concat([pd.Series(leverage, name = 'leverage'),pd.Series(dffits, name = 'dffits'),
pd.Series(resid_stu,name = 'resid_stu'),pd.Series(cook, name = 'cook')],axis = 1)
print(contat1)

# 重设train数据的行索引
train.index = range(train.shape[0])
# 将上面的统计量与train数据集合并
profit_outliers = pd.concat([train,contat1], axis = 1)
print(profit_outliers.head())
# 计算异常值数量的比例
outliers_ratio = sum(np.where((np.abs(profit_outliers.resid_stu)>2),1,0))/profit_outliers.shape[0]
print(outliers_ratio)
# 挑选出非异常的观测点
none_outliers = profit_outliers.ix[np.abs(profit_outliers.resid_stu)<=2,]
print(none_outliers)

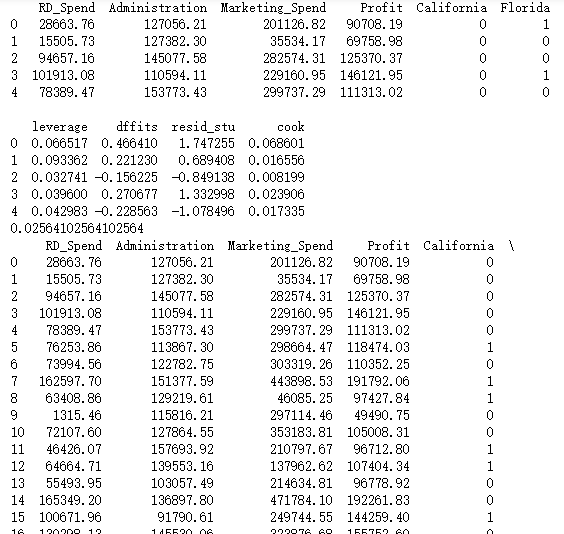
# 应用无异常值的数据集重新建模
model4 = smf.ols('Profit ~ RD_Spend + Marketing_Spend', data = none_outliers).fit()
print(model4.params)
# Durbin-Watson统计量
# 模型概览
print(model4.summary())

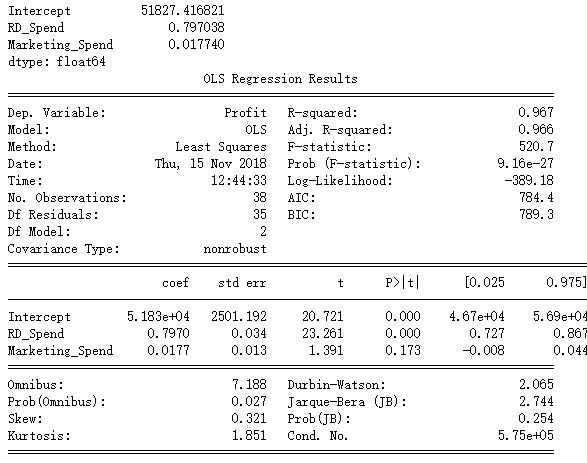
# 方差齐性检验
# 设置第一张子图的位置
ax1 = plt.subplot2grid(shape = (2,1), loc = (0,0))
# 绘制散点图
ax1.scatter(none_outliers.RD_Spend, (model4.resid-model4.resid.mean())/model4.resid.std())
# 添加水平参考线
ax1.hlines(y = 0 ,xmin = none_outliers.RD_Spend.min(),xmax = none_outliers.RD_Spend.max(), color = 'red', linestyles = '--')
# 添加x轴和y轴标签
ax1.set_xlabel('RD_Spend')
ax1.set_ylabel('Std_Residual')

# 设置第二张子图的位置
ax2 = plt.subplot2grid(shape = (2,1), loc = (1,0))
# 绘制散点图
ax2.scatter(none_outliers.Marketing_Spend, (model4.resid-model4.resid.mean())/model4.resid.std())
# 添加水平参考线
ax2.hlines(y = 0 ,xmin = none_outliers.Marketing_Spend.min(),xmax = none_outliers.Marketing_Spend.max(), color = 'red', linestyles = '--')
# 添加x轴和y轴标签
ax2.set_xlabel('Marketing_Spend')
ax2.set_ylabel('Std_Residual')

# 调整子图之间的水平间距和高度间距
plt.subplots_adjust(hspace=0.6, wspace=0.3)
# 显示图形
plt.show()

# BP检验
sm.stats.diagnostic.het_breushpagan(model4.resid, exog_het = model4.model.exog)

# 模型预测
# model4对测试集的预测
pred4 = model4.predict(exog = test.ix[:,['RD_Spend','Marketing_Spend']])
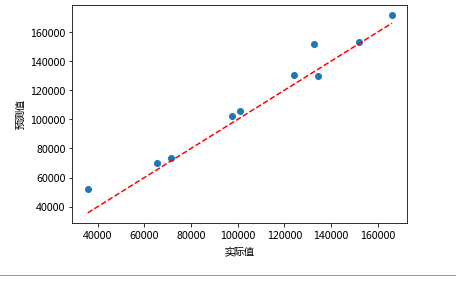
# 绘制预测值与实际值的散点图
plt.scatter(x = test.Profit, y = pred4)
# 添加斜率为1，截距项为0的参考线
plt.plot([test.Profit.min(),test.Profit.max()],[test.Profit.min(),test.Profit.max()],
color = 'red', linestyle = '--')
# 添加轴标签
plt.xlabel('实际值')
plt.ylabel('预测值')
# 显示图形
plt.show()